Считается нераспределенным, если он взят в части объема.

Рассмотрим, как распределены термины в суждениях А,Е, I, О.

1. Суждение А (Все S суть Р). «Все студенты нашей группы (S) сдали экзамены (Р)». Субъект этого суждения («студенты нашей группы») распределен, он взят в полном объеме: речь идет обо всех студентах нашей группы. Предикат этого суждения не распределен, так как в нем мыслится только часть лиц, сдавших экзамены, совпадающая со студентами нашей группы.

Таким образом, в общеутвердительных суждениях S распреде­лен, а Р не распределен. Однако в общеутвердительных суждениях, субъект и предикат которых имеют одинаковый объем, распределен не только субъект, но и предикат. К таким суждениям относятся общевыделяющие суждения, а также определения, подчиняющиеся правилу соразмерности.

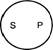
2. Суждение Е (Ни одно S не есть Р). «Ни один студент нашей группы (S) не является неуспевающим (Р)». И субъект, и предикат взяты в полном объеме. Объем одного термина полностью исключа­ется из объема другого: ни один студент нашей группы не входит в число неуспевающих, и ни один неуспевающий не является студен­том нашей группы. Следовательно, в общеотрицательных суждени­ях и S, и Р распределены (рис. 26).

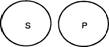
3. Суждение I (Некоторые S суть Р). «Некоторые студенты нашей группы (S) — отличники (Р)». Субъект этого суждения не распре­делен, так как в нем мыслится только часть студентов нашей груп­пы, объем субъекта лишь частично включается в объем предиката:

только некоторые студенты нашей группы относятся к числу от­личников. Но и объем предиката лишь частично включается в объем субъекта: не все, а только некоторые отличники — студенты нашей группы.

Следовательно, в частноутвердительном суждении ни S, ни Р не распределены (рис. 27).

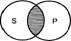
Исключение из этого правила составляют частновыделяющие суждения, предикат которых полностью входит в объем субъекта. Например: «Некоторые родители, и только они (S), являются много­детными (Р)». Здесь понятиe «многодетные» полностью входит в объем понятия «родители». Субъект такого суждения не распреде­лен, предикат распределен (рис. 28).

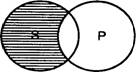
4. Суждение О (некоторые S не суть Р). «Некоторые студенты нашей группы (S) — не отличники (Р)». Субъект этого суждения не распределен (мыслится лишь часть студентов нашей группы), пре­дикат распределен, в нем мыслятся все отличники, ни один из кото­рых не включается в ту часть студентов нашей группы, которая мыслится в субъекте. Следовательно, в частноотрицательном сужде­нии S не распределен, а Р распределен (рис. 29).

73.Понятие сложных суждений неразрывно связано с конъюнкцией, дизъюнкцией, импликацией, эквиваленцией и отрицанием. Это так называемые логические связки. Они используются в качестве объединяющего звена, привязывающего одно простое суждение к другому. Именно так образуются сложные суждения. То есть сложные суждения — это суждения, созданные из двух простых. Конъюнкция (a^b) — это способ связи простых суждений в сложные, при котором истинность полученного суждения напрямую зависит от истинности составных. Истинность таких суждений достигается только тогда, когда оба простых суждения (и a, и b) так же истинны. Если хотя бы одно из данных суждений ложно, то ложным следует признать и образованное из них новое, сложное суждение. Например, в суждении «Этот автомобиль очень качественный (a) и пробежал всего десять тысяч метров (b)» истинность зависит как от его правой стороны, так и от левой. Если оба простых суждения истинны, то истинно и сложное, образованное из них. В противном случае (если хотя бы одно из простых суждений ложно) оно является ложным. Дизъюнкция (a Ъ b) бывает строгой и нестрогой. Отличие между этими двумя видами дизъюнкции состоит в том, что при нестрогом виде члены ее не исключают друг друга. Примером нестрогой дизъюнкции может быть: «Для получения заготовки деталь можно довести на станке (a) или предварительно обработать напильником (b)». Очевидно, что здесь а не исключает b и наоборот. Истинность подобного сложного суждения зависит от истинности его членов следующим образом: если ложны оба члена, ложным признается и образованное при их посредстве дизъюнктивное суждение. Однако, если ложно только одно простое суждение, такая дизъюнкция признается истинной. Эквивалентнция характеризуется тем, что образованное сложное суждение истинно только в тех случаях, когда истинны оба простых суждения, входящих в его состав, и ложно при ложности обоих этих суждений. В буквенном выражении эквивалентность выглядит как a є b. При отрицании суждения, отображающееся как a, истинно тогда, когда ложно отрицаемое понятие. Это связано с тем, что отрицание и отрицаемое простое суждение не только противоречат, но и исключают (отрицают) друг друга. Таким образом, получается, что, когда истинно понятие a, ложно понятие a. И наоборот, если ложно a, то отрицающее его a является истинным. Импликация (a ® b) истинна во всех случаях, кроме одного. Другими словами, если оба входящих в импликацию простых суждения истинны или ложны либо если ложно суждение a, импликация истинна. Однако при ложности суждения b ложным становится и сама импликация. Это можно рассмотреть на примере: «Мы бросим исправный патрон в костер (a), он взорвется (b)». Очевидно, что если первое суждение верно, то верно и второе, так как взрыв патрона, брошенного в костер, произойдет с неизбежностью. 74. Назовите основные группы сложных суждений. В зависимости от того, какие логические союзы используются при образовании сложных суждений, последние делятся на следующие виды: отрицательные, соединительные, разделительные, условные и эквивалентные суждения. Все эти сложные суждения могут быть истинными и ложными. Но их истинность (ложность) зависит от истинности (ложности) простых суждений и смысла логических союзов, с помощью которых они образуются. Точный смысл логических союзов определяется с помощью, так называемых таблиц истинности.     75. Объясните на примерах суть конъюнктивного, слабого (нестрогого) дизъюнктивного, сильного (строгого) дизъюнктивного, импликативного и эквивалентного суждений, продемонстрируйте их символы. Суждение — мысль, выражаемая повествовательным предложением и являющаяся истинной или ложной. КОНЪЮНКЦИЯ (от лат. conjunctio - союз, связь) Соединительные (конъюнктивные) суждения — состоят из нескольких простых, связанных логической связкой «и» (р٨q), где p,q — конъюнкты: Кража и мошенничество относятся к умышленным преступлениям (а, но, а также, как и, одновременно). Может быть многосоставным: р٨q٨r٨...٨n. Соединительное суждение истинно при истинности всех составляющих его конъюнктов и ложно при ложности хотя бы одного из них. Символически конъюнктивная связка обозначается знаками « ∙ », «&», «Ù». Если А, В, С... представляют простые высказывания, то конъюнктивное высказывание выглядит следующим образом: А&В или А&В&С и т. п. В обыденной речи К. соответствует союз «и», поэтому К. читается так: А и В. Напр.: «Пассажиры заняли свои места, и поезд тронулся». Соединительное суждение может быть выражено одной из трех логико-грамматических структур: 1.Соединительная связка представлена в сложном субъекте — S1 и S2 есть P — Конфискация имущества и лишения звания являются дополнительными уголовно-правовыми санкциями; 2.Соединительная связка представлена в сложном предикате — S есть Р1 и Р2 — Преступление — это общественно опасное и противоправное деяние; 3.Соединительная связка представлена в сложном предикате и сложном субъекте — S1 и S2 есть Р1 и Р2 — «С полицмейстером и прокурором Ноздрев тоже был на «ты» и общался по-дружески» (Н.В. Гоголь). конъюнктивное высказывание истинно только в одном случае, когда все входящие в него простые высказывания истинны. Напр., высказывание «Киев стоит на Днепре, и Киев — столица Украины» истинно, а высказывание «Киев стоит на Днепре, и Киев - столица Белоруссии» ложно. Следует иметь в виду, что К. учитывает только истинностные значения простых высказываний и не учитывает смысловые связи между ними. Поэтому К. может соединять высказывания, между которыми нет никакой содержательной связи. Напр., «Дважды два четыре, и снег бел» и т. п. Для К. справедлив закон коммутативности: А&В эквивалентно В&А, хотя в высказываниях с союзом «и» этот закон действует далеко не всегда. Напр., если в высказывании «Подул ветер, и деревья закачались» поменять местами члены К., высказывание станет бессмысленным с точки зрения здравого смысла. Разделительные (дизъюнктивные) суждения —состоят из нескольких простых, связанных логической связкой «или» (р۷q), p,q — члены дизъюнкции. Многосоставное: р۷q۷r۷...۷n.   Разделительное суждение может быть выражено одной из трех логико-грамматических структур: 1. Разделительная связка представлена в сложном субъекте - S1 или S2 есть P — Хищение в крупных размерах или совершенное группой лиц имеет повышенную общественную опасность; 1.Разделительная связка представлена в сложном предикате — S есть Р1 или Р2 — Хищение наказывается исправительными работами или тюремным заключением; 2.Разделительная связка представлена в сложном предикате и сложном субъекте — S1 или S2 есть Р1 или Р2 — Ссылка или высылка могут применяться в качестве основной или дополнительной санкции. Нестрогая (слабая) дизъюнкция — связка «или» употребляется в соединительно-разделительном значении. Холодное оружие может быть колющим или режущим («или» разделяет, так как отдельно существуют колющее оружие и режущее оружие; соединяет, так как есть оружие одновременно и колющее и режущее). Условия истинности нестрогой дизъюнкции — суждение будет истинно при истинности хотя бы одного члена дизъюнкции, и ложно при ложности обоих ее членов. Строгая (сильная) дизъюнкция — связка «или» употребляется в разделительном значении (или... или...; либо..., либо...). Деяние может быть умышленным или неосторожным. Члены строгой дизъюнкции (альтернативы) не могут быть одновременно истинными. Если деяние совершено умышленно, его нельзя считать неосторожным и наоборот. Условия истинности строгой дизъюнкции— суждение будет истинно при истинности одного и ложности другого члена дизъюнкции и ложно, если оба члена истинны или оба ложны. Полная (закрытая) дизъюнкция — перечислены все признаки или все виды определенного рода <p v q v r>. Леса бывают лиственные, хвойные или смешанные (других видов не существует). Неполная (открытая) дизъюнкция — перечислены не все признаки или не все виды определенного рода p v q v r... (и т.д.; и др.; и т.п.; иные). В рамках логики высказываний (раздел классической математической логики) различают слабую (нестрогую) Д. и сильную (строгую) Д. Если A и В - высказывания, а знак v - знак нестрогой Д., то высказывание «A Ú B» называют нестрогой Д. (читается: «A или В»). Если Ú — знак строгой Д., то высказывание «A Ú В» называют строгой Д. (читается: «либо А, либо В»). Высказывание «A Ú В» истинно в том и только в том случае, когда истинно по крайней мере одно из составляющих его высказываний, и ложно, когда оба составляющие его высказывания ложны. Высказывание «A Ú В» истинно в том случае, когда истинно одно и только одно из составляющих его высказываний, и ложно в остальных случаях. Условные (импликативные) суждения— состоят из нескольких простых, связанных логической связкой «если..., то...» (р→q), где р — антецедент (предшествующий) выполняет функцию фактического или логического основания, q — консеквент (последующий). Если предохранитель плавится (р), то электролампа гаснет (q) (там..., где; тогда..., когда...; постольку..., поскольку; при наличии..., следует...; в случае..., следует...; при условии..., наступает...).   Условие истинности импликации — импликация истинна во всех случаях, кроме одного: при истинности антецедента (р — если...) и ложности консеквентна (q — то...) импликация будет ложной. Эквивалентные суждения (двойная импликация) — включают в качестве составных два суждения, связанных двойной (прямой и обратной) зависимостью, выражаемой логической связкой «если и только если..., то...» (двойная импликация: р↔q «Если и только если р, то q» или знаком эквивалентности р≡q) (лишь при условии что..., то...; в том и только в том случае когда..., тогда...; только тогда когда..., то...). Если и только если человек награжден орденами медалями (р), то он имеет право на ношение соответствующих орденских планок (q). Истинность утверждения о награждении (р) — необходимое и достаточное условие истинности утверждения о наличии права на ношение орденских планок (q) и наоборот. 75. Объясните на примерах суть конъюнктивного, слабого (нестрогого) дизъюнктивного, сильного (строгого) дизъюнктивного, импликативного и эквивалентного суждений, продемонстрируйте их символы. Суждение — мысль, выражаемая повествовательным предложением и являющаяся истинной или ложной. КОНЪЮНКЦИЯ (от лат. conjunctio - союз, связь) Соединительные (конъюнктивные) суждения — состоят из нескольких простых, связанных логической связкой «и» (р٨q), где p,q — конъюнкты: Кража и мошенничество относятся к умышленным преступлениям (а, но, а также, как и, одновременно). Может быть многосоставным: р٨q٨r٨...٨n. Соединительное суждение истинно при истинности всех составляющих его конъюнктов и ложно при ложности хотя бы одного из них. Символически конъюнктивная связка обозначается знаками « ∙ », «&», «Ù». Если А, В, С... представляют простые высказывания, то конъюнктивное высказывание выглядит следующим образом: А&В или А&В&С и т. п. В обыденной речи К. соответствует союз «и», поэтому К. читается так: А и В. Напр.: «Пассажиры заняли свои места, и поезд тронулся». Соединительное суждение может быть выражено одной из трех логико-грамматических структур: 1.Соединительная связка представлена в сложном субъекте — S1 и S2 есть P — Конфискация имущества и лишения звания являются дополнительными уголовно-правовыми санкциями; 2.Соединительная связка представлена в сложном предикате — S есть Р1 и Р2 — Преступление — это общественно опасное и противоправное деяние; 3.Соединительная связка представлена в сложном предикате и сложном субъекте — S1 и S2 есть Р1 и Р2 — «С полицмейстером и прокурором Ноздрев тоже был на «ты» и общался по-дружески» (Н.В. Гоголь). конъюнктивное высказывание истинно только в одном случае, когда все входящие в него простые высказывания истинны. Напр., высказывание «Киев стоит на Днепре, и Киев — столица Украины» истинно, а высказывание «Киев стоит на Днепре, и Киев - столица Белоруссии» ложно. Следует иметь в виду, что К. учитывает только истинностные значения простых высказываний и не учитывает смысловые связи между ними. Поэтому К. может соединять высказывания, между которыми нет никакой содержательной связи. Напр., «Дважды два четыре, и снег бел» и т. п. Для К. справедлив закон коммутативности: А&В эквивалентно В&А, хотя в высказываниях с союзом «и» этот закон действует далеко не всегда. Напр., если в высказывании «Подул ветер, и деревья закачались» поменять местами члены К., высказывание станет бессмысленным с точки зрения здравого смысла. Разделительные (дизъюнктивные) суждения —состоят из нескольких простых, связанных логической связкой «или» (р۷q), p,q — члены дизъюнкции. Многосоставное: р۷q۷r۷...۷n.   Разделительное суждение может быть выражено одной из трех логико-грамматических структур: 1. Разделительная связка представлена в сложном субъекте - S1 или S2 есть P — Хищение в крупных размерах или совершенное группой лиц имеет повышенную общественную опасность; 1.Разделительная связка представлена в сложном предикате — S есть Р1 или Р2 — Хищение наказывается исправительными работами или тюремным заключением; 2.Разделительная связка представлена в сложном предикате и сложном субъекте — S1 или S2 есть Р1 или Р2 — Ссылка или высылка могут применяться в качестве основной или дополнительной санкции. Нестрогая (слабая) дизъюнкция — связка «или» употребляется в соединительно-разделительном значении. Холодное оружие может быть колющим или режущим («или» разделяет, так как отдельно существуют колющее оружие и режущее оружие; соединяет, так как есть оружие одновременно и колющее и режущее). Условия истинности нестрогой дизъюнкции — суждение будет истинно при истинности хотя бы одного члена дизъюнкции, и ложно при ложности обоих ее членов. Строгая (сильная) дизъюнкция — связка «или» употребляется в разделительном значении (или... или...; либо..., либо...). Деяние может быть умышленным или неосторожным. Члены строгой дизъюнкции (альтернативы) не могут быть одновременно истинными. Если деяние совершено умышленно, его нельзя считать неосторожным и наоборот. Условия истинности строгой дизъюнкции— суждение будет истинно при истинности одного и ложности другого члена дизъюнкции и ложно, если оба члена истинны или оба ложны. Полная (закрытая) дизъюнкция — перечислены все признаки или все виды определенного рода <p v q v r>. Леса бывают лиственные, хвойные или смешанные (других видов не существует). Неполная (открытая) дизъюнкция — перечислены не все признаки или не все виды определенного рода p v q v r... (и т.д.; и др.; и т.п.; иные). В рамках логики высказываний (раздел классической математической логики) различают слабую (нестрогую) Д. и сильную (строгую) Д. Если A и В - высказывания, а знак v - знак нестрогой Д., то высказывание «A Ú B» называют нестрогой Д. (читается: «A или В»). Если Ú — знак строгой Д., то высказывание «A Ú В» называют строгой Д. (читается: «либо А, либо В»). Высказывание «A Ú В» истинно в том и только в том случае, когда истинно по крайней мере одно из составляющих его высказываний, и ложно, когда оба составляющие его высказывания ложны. Высказывание «A Ú В» истинно в том случае, когда истинно одно и только одно из составляющих его высказываний, и ложно в остальных случаях. Условные (импликативные) суждения— состоят из нескольких простых, связанных логической связкой «если..., то...» (р→q), где р — антецедент (предшествующий) выполняет функцию фактического или логического основания, q — консеквент (последующий). Если предохранитель плавится (р), то электролампа гаснет (q) (там..., где; тогда..., когда...; постольку..., поскольку; при наличии..., следует...; в случае..., следует...; при условии..., наступает...).   Условие истинности импликации — импликация истинна во всех случаях, кроме одного: при истинности антецедента (р — если...) и ложности консеквентна (q — то...) импликация будет ложной. Эквивалентные суждения (двойная импликация) — включают в качестве составных два суждения, связанных двойной (прямой и обратной) зависимостью, выражаемой логической связкой «если и только если..., то...» (двойная импликация: р↔q «Если и только если р, то q» или знаком эквивалентности р≡q) (лишь при условии что..., то...; в том и только в том случае когда..., тогда...; только тогда когда..., то...). Если и только если человек награжден орденами медалями (р), то он имеет право на ношение соответствующих орденских планок (q). Истинность утверждения о награждении (р) — необходимое и достаточное условие истинности утверждения о наличии права на ношение орденских планок (q) и наоборот.