Определение 1. Пусть и произвольные множества. Соответствием называется тройка множеств 2 страница
Замечание 5. В примере 5.1 была рассмотрена четырехзначная логическая функция – ее область прибытия (а также и область значений) состояла из четырех элементов. Однако многозначную логическую функцию всегда можно заменить двузначными. В частности, функцию 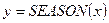 из примера 5.1 можно заменить четырьмя такими
из примера 5.1 можно заменить четырьмя такими 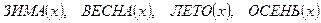 , которые могут принимать только два значения ДА или НЕТ (истинно или ложно).
, которые могут принимать только два значения ДА или НЕТ (истинно или ложно).
Замечание 6.Всюду определенные логические функции двузначной логики разбивают свою область отправления на две части – область истинности и область ложности. Например, признак 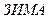 для названий месяцев разделит всё множество месяцев на два подмножества {январь, февраль, декабрь} - область истинности и {март, апрель, май, июнь, июль, август, сентябрь, октябрь, ноябрь} - область ложности. Однако для не всюду определенной логической функции к этим областям еще добавится область неопределенности (см. замечание 3).
для названий месяцев разделит всё множество месяцев на два подмножества {январь, февраль, декабрь} - область истинности и {март, апрель, май, июнь, июль, август, сентябрь, октябрь, ноябрь} - область ложности. Однако для не всюду определенной логической функции к этим областям еще добавится область неопределенности (см. замечание 3).
Вопросы для самоконтроля
1. Определите область истинности функций 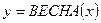 ,
, 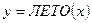 ,
, 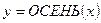 , которые определены на множестве названий месяцев.
, которые определены на множестве названий месяцев.
2. Составьте соответствие, определяющее цвет граней некоторого заданного
куба. Будет ли функция COLOR(g) , задающая цвет грани куба, свойством?
5.1.4. Бинарные отношения
Бинарные отношения и способы их задания
Определение 3. Двуместная логическая функция двузначной логики с одинаковыми алфавитами для вхождений называется бинарным отношением.
Иначе говоря, бинарное отношение – это однозначное соответствие вида
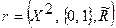 , (5.4)
, (5.4)
где 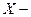 алфавит вхождений (область изменения независимых переменных
алфавит вхождений (область изменения независимых переменных  и
и 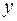 логической функции
логической функции 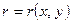 , определяемой соответствием (5.4) по закону (графику)
, определяемой соответствием (5.4) по закону (графику) 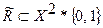 ). Элементы из X могут иметь любую природу.
). Элементы из X могут иметь любую природу.
Задать бинарное отношение можно перечислением всех элементов из множества 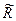 , содержащего тройки
, содержащего тройки 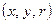 с компонентами
с компонентами 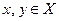 ,
, 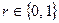 . Однако такой способ не самый удобный. Проще перечислить пары вида
. Однако такой способ не самый удобный. Проще перечислить пары вида 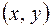 , определяющие область истинности данного отношения, а в случае, если бинарное отношение не всюду определено (
, определяющие область истинности данного отношения, а в случае, если бинарное отношение не всюду определено ( 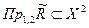 ), – еще и все пары области ложности. Область истинности
), – еще и все пары области ложности. Область истинности  бинарного отношения
бинарного отношения 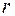 определится выражением
определится выражением
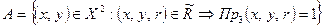 , (5.5)
, (5.5)
а область ложности – соответственно выражением
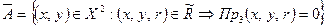 . (5.6)
. (5.6)
Из (5.5) и (5.6) следует, что 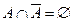 и
и 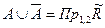 , а когда бинарное отношение всюду определено (
, а когда бинарное отношение всюду определено ( 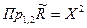 ), то
), то 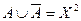 . Иначе говоря, всюду (не всюду) определенное бинарное отношение задано тогда, когда задан алфавит
. Иначе говоря, всюду (не всюду) определенное бинарное отношение задано тогда, когда задан алфавит  для независимых переменных
для независимых переменных  и
и 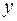 (а также область ложности
(а также область ложности 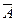 или область определения
или область определения 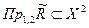 , или область неопределенности
, или область неопределенности 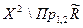 ) и область истинности
) и область истинности  .
.
Далее будем рассматривать в основном только всюду определенные бинарные отношения и для краткости будем называть их (если нет специальных на то оговорок) просто отношениями. Тогда из наших рассуждений следует, что отношение можно задать парой множеств
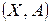 ,
, 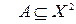 , (5.7)
, (5.7)
где 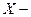 множество элементов произвольной природы, на котором задано отношение
множество элементов произвольной природы, на котором задано отношение 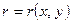 , где
, где 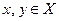 , а
, а  область истинности этого отношения (при этом его область ложности
область истинности этого отношения (при этом его область ложности 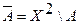 ). Таким образом, задача задания на некотором известном множестве
). Таким образом, задача задания на некотором известном множестве  отношения с областью истинности
отношения с областью истинности  у нас попросту свелась к задаче задания одного лишь множества
у нас попросту свелась к задаче задания одного лишь множества 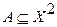 . Если это множество задано, то закон (график) отношения определится по формуле
. Если это множество задано, то закон (график) отношения определится по формуле
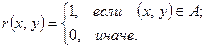 (5.8)
(5.8)
Задать область  можно, кроме простого перечисления ее элементов, квадратной двузначной матрицей размерностью
можно, кроме простого перечисления ее элементов, квадратной двузначной матрицей размерностью 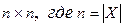 , т.е. таблицей вида
, т.е. таблицей вида
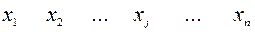
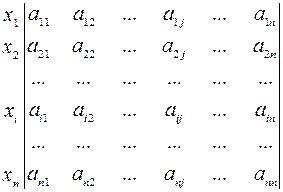
Каждый элемент 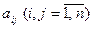 данной матрицы равен либо нулю, либо единице. При этом если элемент
данной матрицы равен либо нулю, либо единице. При этом если элемент 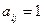 , то пара
, то пара 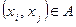 , и
, и 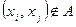 (т.е.
(т.е. 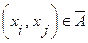 ), если
), если 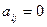 .
.
Пример 5.3. Пусть на множестве 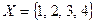 задано отношение с областью истинности
задано отношение с областью истинности 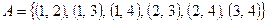 . Тогда данное отношение можно задать следующей матрицей:
. Тогда данное отношение можно задать следующей матрицей:
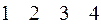
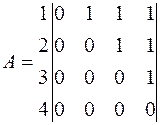 . (5.9)
. (5.9)
Каков смысл данного отношения? Его область истинности составляют все те, и только те пары, в которых первая компонента меньше второй. Следовательно, матрица (5.9) задает на числах 1, 2, 3 и 4 отношение «меньше».
Замечание 1.В данном примере область истинности отношения и двоичная матрица, которая эту область определяет, обозначены одним и тем же символом. С целью упрощения наших обозначений условимся еще и знак самого отношения обозначать тем же символом  . Ранее имя отношения у нас обозначалось буквой
. Ранее имя отношения у нас обозначалось буквой 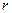 . Теперь мы и его станем обозначать буквой
. Теперь мы и его станем обозначать буквой  . При этом совершенно равнозначными будут следующие условия:
. При этом совершенно равнозначными будут следующие условия:
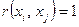 ,
, 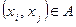 ,
, 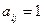 ,
, 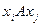 .
.
Здесь во втором условии под символом  подразумевается множество пар (область истинности), в четвертом этот символ означает знак отношения между двумя элементами (аналогично тому, когда пишут
подразумевается множество пар (область истинности), в четвертом этот символ означает знак отношения между двумя элементами (аналогично тому, когда пишут 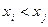 ), а третье условие указывает на то, что в
), а третье условие указывает на то, что в 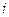 -й строке
-й строке 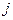 -го столбца матрицы
-го столбца матрицы  стоит единица. Также равнозначными являются и такие условия:
стоит единица. Также равнозначными являются и такие условия:
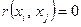 ,
, 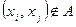 ,
, 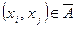 ,
, 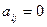 ,
, 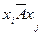 или
или 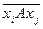 .
.
В третьем условии обозначение 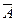 определяет область ложности (5.6), т.е. множество пар
определяет область ложности (5.6), т.е. множество пар 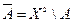 , а в пятом – знак отношения, у которого областью истинности является область ложности отношения
, а в пятом – знак отношения, у которого областью истинности является область ложности отношения 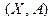 . Шестое условие – это отрицание условия
. Шестое условие – это отрицание условия 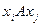 (в математическом языке знак отрицания условия может совпадать со знаком дополнения множества).
(в математическом языке знак отрицания условия может совпадать со знаком дополнения множества).
Отношения могут иметь и графическое представление. Его называют графом. При построении графа для некоторого отношения 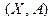 сначала изображаются в виде точек элементы множества
сначала изображаются в виде точек элементы множества  (их называют вершинами графа). Затем те пары вершин, для которых выполнено условие
(их называют вершинами графа). Затем те пары вершин, для которых выполнено условие 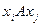 , соединяются стрелочками в направлении от вершины
, соединяются стрелочками в направлении от вершины 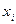 к вершине
к вершине 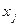 (пару (
(пару ( 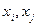 ) называют дугой, т.е.
) называют дугой, т.е.  множество дуг графа).
множество дуг графа).

 В частности, для отношения из примера 5.3можно построить граф, который будет задавать данное отношение графически (рис. 5.4).
В частности, для отношения из примера 5.3можно построить граф, который будет задавать данное отношение графически (рис. 5.4).

 Таким образом, отношения можно задавать либо простым перечислением элементов множеств
Таким образом, отношения можно задавать либо простым перечислением элементов множеств  и
и  , либо двоичной квадратной матрицей, либо в виде графа.
, либо двоичной квадратной матрицей, либо в виде графа.
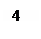
|
Вопросы для самоконтроля
1. Задайте тремя способами отношение «быть больше» на множестве 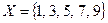 .
.
2. Определите область истинности отношения «быть подмножеством», заданного на множестве  всех подмножеств множества
всех подмножеств множества 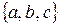 .
.
Операции над отношениями
Отношение задается областью истинности, т.е. множеством пар. Используя операции над множествами, можно из одних отношений получать другие.
Ниже будем рассматривать лишь отношения с общей для всех областью определения  (множество
(множество  считается уже заданным). Именно над такими отношениями мы и будем осуществлять операции. Тогда отношение можно будет обозначать не парой
считается уже заданным). Именно над такими отношениями мы и будем осуществлять операции. Тогда отношение можно будет обозначать не парой  , а просто одним символом
, а просто одним символом  .
.
Определение 4. Отношение 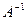 называется обратным отношению
называется обратным отношению  , если его область истинности получается из области истинности отношения
, если его область истинности получается из области истинности отношения  в результате возведения ее в минус первую степень.
в результате возведения ее в минус первую степень.
Отметим, что формула 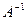 одновременно означает и отношение, обратное отношению
одновременно означает и отношение, обратное отношению  , и множество пар
, и множество пар  в степени -1, и операцию транспонирования матрицы (преобразование матрицы, заключающееся в том, что ее строки заменяются столбцами, а столбцы – строками).
в степени -1, и операцию транспонирования матрицы (преобразование матрицы, заключающееся в том, что ее строки заменяются столбцами, а столбцы – строками).
Пример 5.4. Найти обратное отношение для отношения из примера 5.3.
Решение. Дано отношение «меньше», для которого область истинности 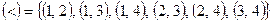 . Возведем ее в степень -1. Получим
. Возведем ее в степень -1. Получим 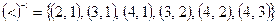 . Данное множество соответствует двоичной матрице, которая получится при транспонировании матрицы (5.9), т.е.
. Данное множество соответствует двоичной матрице, которая получится при транспонировании матрицы (5.9), т.е.
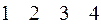
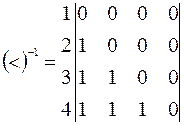 . (5.10)
. (5.10)
В результате имеем отношение «больше», т.к. в область истинности данного отношения попали все те и только те пары, у которых первая компонента строго больше второй. Таким образом, отношение 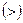 может быть задано и формулой
может быть задано и формулой 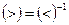 , т.е. аналитически.
, т.е. аналитически.
Из того, что для любого множества  пар справедливо
пар справедливо 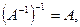 следует, что обратным для обратного отношения является исходное.
следует, что обратным для обратного отношения является исходное.
Определение 5. Отношение 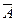 называется противоположным отношению
называется противоположным отношению  , если его область истинности равна области ложности отношения
, если его область истинности равна области ложности отношения  .
.
Пример 5.5. Найти противоположное отношение для отношения из примера 5.3.
Решение. Область истинности этого отношения 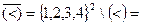
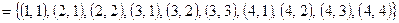 .
.
Данное множество соответствует двоичной матрице, которая получится из матрицы (5.9), если в ней все единицы заменить нулями, а нули единицами, т.е.
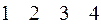
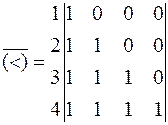 .
.
По смыслу это будет отношение «не меньше» («больше либо равно»). Его аналитическое задание можно представить формулой 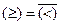 .
.
Нетрудно видеть, что противоположным от противоположного отношения будет исходное.
Пример 5.6. Найти противоположное отношение для отношения из примера 5.4 (т.е. противоположное от обратного для отношения «меньше»).
Решение. Найдем его область истинности 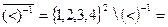
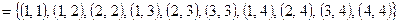 . Данное множество соответствует двоичной матрице, которая получится из матрицы (5.10), если в ней все единицы заменить нулями, а нули единицами, т.е.
. Данное множество соответствует двоичной матрице, которая получится из матрицы (5.10), если в ней все единицы заменить нулями, а нули единицами, т.е.
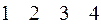
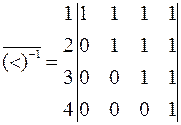 .
.
Получилось отношение «не больше» («меньше либо равно»), которое можно определить формулой 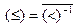 .
.
Определениe 6. Совмещением двух отношений  и
и  называется отношение
называется отношение 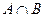 , область истинности которого равна пересечению областей истинности отношений
, область истинности которого равна пересечению областей истинности отношений  и
и 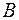 .
.
Пример 5.7. Найти совмещение отношений 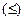 и
и 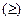 .
.
Решение. Найдем область истинности отношения 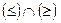 .
. 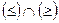
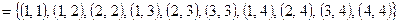
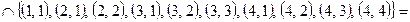
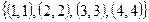 .
.
Данное множество соответствует двоичной матрице с единицами только по главной диагонали. Ее называют единичной матрицей. Введем для нее обозначение – 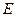
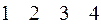
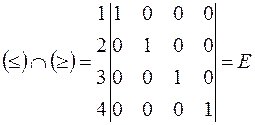 .
.
По смыслу это отношение равенства. Его также можно выразить через отношение «меньше», а именно:
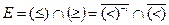 .
.
Определение 7. Объединением двух отношений  и
и  называется отношение
называется отношение 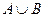 , область истинности которого равна объединению областей истинности отношений
, область истинности которого равна объединению областей истинности отношений  и
и  .
.
Например, 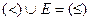 ,
, 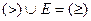 .
.
Определение 8. Композицией двух отношений  и
и 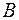 называется отношение
называется отношение 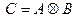 , область истинности которого определяется двоичной матрицей
, область истинности которого определяется двоичной матрицей  , полученной из матриц
, полученной из матриц  и
и  по следующим формулам:
по следующим формулам:
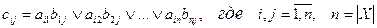 . (5.11)
. (5.11)
Композицию какого-либо отношения  на себя будем обозначать
на себя будем обозначать 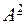 , т.е.
, т.е. 
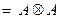 . И далее по аналогии
. И далее по аналогии 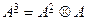 , …,
, …, 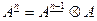 .
.
Замечание 1.Не нужно путать 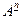 и
и 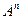 . Ведь
. Ведь 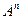 - это множество
- это множество 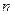 -ок, компонентами которых являются элементы множества
-ок, компонентами которых являются элементы множества  , т.е. пары, а
, т.е. пары, а 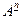 - область истинности отношения (множество пар, а не
- область истинности отношения (множество пар, а не  -ок из пар).
-ок из пар).
Определение 9. Транзитивным замыканием отношения  называют отношение
называют отношение  .
.
Пример 5.8. Найти транзитивное замыкание отношения «быть меньше ровно на единицу» с областью определения 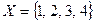 .
.
Решение. Область истинности этого отношения содержит только три пары 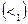
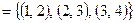 , что соответствует двоичной матрице
, что соответствует двоичной матрице
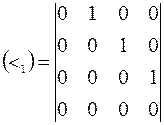 . Тогда
. Тогда 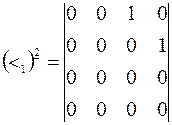 .
.
Здесь элементы матрицы 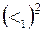 были вычислены по формулам (5.11):
были вычислены по формулам (5.11):
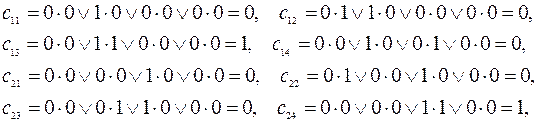
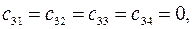 т.к. третья строка имеет только один четвертый элемент, равный единице, а у всех столбцов четвертый элемент равен нулю.
т.к. третья строка имеет только один четвертый элемент, равный единице, а у всех столбцов четвертый элемент равен нулю.
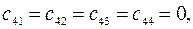 т.к. четвертая строка матрицы
т.к. четвертая строка матрицы 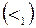 состоит из одних нулей.
состоит из одних нулей.
Следовательно, 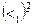
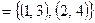 , т.е. область истинности отношения
, т.е. область истинности отношения 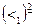 содержит все те и только те пары из множества
содержит все те и только те пары из множества 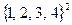 , у которых первая компонента меньше второй ровно на два.
, у которых первая компонента меньше второй ровно на два.
Аналогично вычислим матрицы 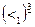 и
и 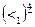 . Получим
. Получим
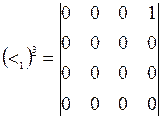 и
и 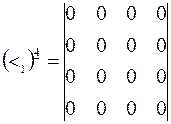 .
.
Поэтому область 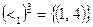 будет определять отношение «быть меньше ровно на три», а
будет определять отношение «быть меньше ровно на три», а 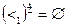 , т.е. на множестве
, т.е. на множестве 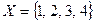 ни один из элементов не может быть больше другого ровно на четыре. Тем более
ни один из элементов не может быть больше другого ровно на четыре. Тем более 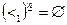 при
при 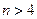 . Тогда транзитивным замыканием отношения «быть меньше ровно на единицу» с областью определения
. Тогда транзитивным замыканием отношения «быть меньше ровно на единицу» с областью определения 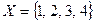 будет следующее:
будет следующее:
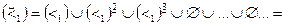
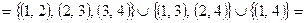
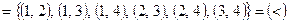 ,
,
т.е. это будет отношение «меньше».
Очевидно, если  - это отношение «быть отцом», то
- это отношение «быть отцом», то 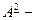 отношение «быть дедом»,
отношение «быть дедом», 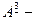 отношение «быть прадедом» и т.д., а
отношение «быть прадедом» и т.д., а 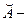 отношение «быть предком». Аналогично транзитивным замыканием отношения «быть сыном» будет отношение «быть потомком».
отношение «быть предком». Аналогично транзитивным замыканием отношения «быть сыном» будет отношение «быть потомком».
