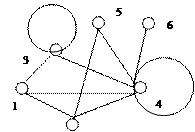
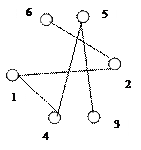
Примеры выполнения заданий. Докажите, что валентности вершин графов А и Б совпадают
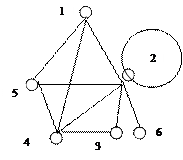
Докажите, что валентности вершин графов А и Б совпадают.
 |

А Б
Решение: А) d(v1)=2, d(v2)=3, d(v3)=3, d(v4)=2, d(v5)=3, d(v6)=3.
Б) d(v1)=2, d(v2)=3, d(v3)=3, d(v4)=2, d(v5)=3, d(v6)=3.
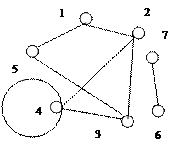
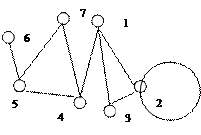
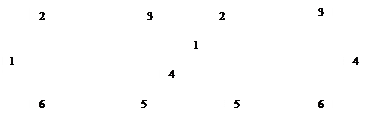
Докажите, что графы G1(X1, E1)и G2(Y2,E2)изоморфны.
 
    |
 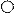
  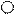  |
Решение:
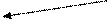 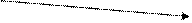 X1(3, 3) X1(3, 3) |  X2(4, 4) X2(4, 4) |   X3(3, 3) X3(3, 3) | X4(2, 2) | X5(2, 2) |
| Y1(4, 4) | Y2(2, 2) | Y3(3, 3) | Y4(3, 3) | Y5(2,2) |
В результате получим соответствие:

Следовательно, графы G1(X, E) и G2(Y, E)изоморфны.
Решите задачу по вычислению валентности вершин графа
Школьник сказал своему приятелю: - У нас в классе 35 человек. Каждый из них дружит ровно с 11 одноклассниками.
Не может этого быть, - сразу ответил приятель, победитель математической олимпиады. Почему он так решил?
Решение: представим себе, что между каждыми двумя друзьями протянута ниточка. Тогда каждый из 35 учеников будет держать в руке 11 концов ниточек, и значит, всего у протянутых ниточек будет 11∙  35 = 385 концов. Но общее число не может быть нечётным, так как у каждой ниточки 2 конца.
35 = 385 концов. Но общее число не может быть нечётным, так как у каждой ниточки 2 конца.
Задания для самостоятельного выполнения
Докажите, что валентности вершин графов А и Б совпадают.
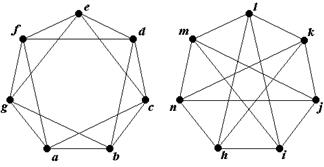
А Б
2. Подсчитайте валентность вершин:
0)Решение: 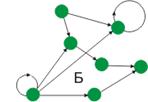 | 1)Решение: 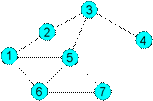 | ||||||
2)Решение:  | 3)Решение:  | ||||||
4)Решение:   А А
С В | 5)  Решение: Решение:    А В А В 
С Д | ||||||
6)Решение: 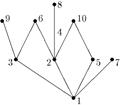 | 7)Решение:     А В А В
С Д | ||||||
8)Решение:   | 9)Решение:
С Д |
4. Определите виды графов и подсчитайте валентность вершин:
0)Решение:
| 1)Решение:
| ||||||||||||||||||||||||
2)Решение:
| 3)Решение:  | ||||||||||||||||||||||||
4)Решение:
| 5) Решение:
   
 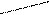
 | ||||||||||||||||||||||||
6)Решение:
| 7)Решение:
| ||||||||||||||||||||||||
8)Решение: 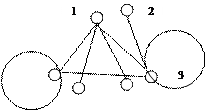
| 9)Решение:  |
Неориентированные графы
Неориентированный граф G (V, E) – это непустое конечное множество вершин (узлов) Vи набор неупорядоченных пар вершин (ребер) E.
Способы задания графа:
1) аналитический (в виде алгебраической системы);
2) геометрический (в виде произвольного рисунка);
3) матричный (в виде матриц смежности и инцидентности).
Пусть v1, v2, ...vn- вершины графа G (V, E), а e1, e2, ...em- его ребра.
Матрицей смежности для неориентированного графа G называется матрица A(G)= ||aij||, i=1,...,n; j = 1, ..., n, у которой элемент aij равен числу ребер, соединяющих вершины vi и vj (соответственно, идущих из вершины vi в вершину vj).
Свойства матрицы смежности:
1) симметричная относительно главной диагонали,
2) значениями являются натуральные числа один и ноль
3) количество петель записывается на главной диагонали,
4) сумма значений по строке или в столбце равна валентности вершины.
Матрицей инцидентности для неориентированного графа с n вершинами и m ребрами называется матрица В(G) = [bij], i=1, 2,..., n, j = 1,2,..., m, строки которой соответствуют вершинам, а столбцы - ребрам. Элемент bij=1, если вершина vi инцидентна ребру ej и bij=0, если вершина vi не инцидентна ребру ej.
Свойства матрицы инцидентности:
1) несимметричная,
2) значениями являются ноль и единица,
3) сумма значений по строке или в столбце равна 2, если нет петель.

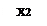





 А В
А В