Домашняя самостоятельная работа №5
«Сложные суждения. Построение таблиц истинности сложных суждений»
Задание №1. Пусть а есть высказывание «9 — четное число» и b — высказывание «9 — нечетное число». Определите значения истинности следующих высказываний:
а) а  b, д) a
b, д) a  b, и) a
b, и) a 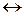 b, н) (а
b, н) (а 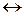 b),
b),
б) b  а, е) b
а, е) b  а, к) a
а, к) a 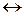 b, о) (а
b, о) (а  b),
b),
в) а  Ь, ж) b
Ь, ж) b  a, л) а
a, л) а 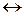 b, п) (а
b, п) (а  b),
b),
г) а  6, з) а
6, з) а 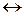 b, м) (а
b, м) (а  b), р) (а
b), р) (а  b).
b).
(максимальное количество баллов - 16)
Задание №2. Используя таблицы истинности для логических связок, определите истинностное значение приведенных сложных высказываний, предполагая, что а — истинное высказывание:
а) а \/ а, е) а & а,
б) а & а, ж) (а  а),
а),
в) а  а, з) (а \/а),
а, з) (а \/а),
г) a 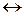 а, и) (а & а),
а, и) (а & а),
д) а \/ а, к) а  а.
а.
(максимальное количество баллов - 10)
Задание №2. Укажите истинное значение приведенных в предыдущем примере сложных высказываний, предполагая, что а — ложное высказывание.
(максимальное количество баллов - 10)
Задание №3. Определите с помощью таблиц истинности, какие из приведенных формул являются тавтологиями:
а) (a 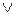 b)
b) 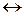 (b
(b 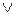 a), з) (а
a), з) (а  b)
b) 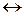 (a & b),
(a & b),
б) (а &b) 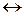 (b&а), и) (а \/ b)
(b&а), и) (а \/ b) 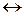 (а
(а  b),
b),
в) (а  b)
b)  (b
(b  а), к) (a \/ b)
а), к) (a \/ b) 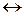 (а & b),
(а & b),
г) (а  b)& b
b)& b  a, л) (a & b)
a, л) (a & b) 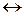 (а \/ b) ,
(а \/ b) ,
д) (а  b)
b)  (b
(b  а), м) (а & b)
а), м) (а & b) 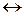 (а
(а  b),
b),
e) (а  b) & a
b) & a  b, н) (а
b, н) (а  b) &(b
b) &(b  a)
a) 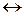 (a
(a 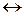 b)
b)
ж) (а  b)
b) 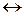 (a
(a 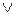 b),
b),
(максимальное количество баллов -13)
Задание №4. Определите, какие из приведенных высказываний являются тавтологиями:
а) Если Иванов здоров, то он здоров и богат.
б) Если Иванов здоров, то он здоров или богат.
в) Если Иванов здоров и богат, то он здоров.
г) Если Иванов здоров или богат, то он здоров.
д) Неверно, что число делится на 2 и на 3, только еслионо неделится на 2 или не делится на 3.
е) Неверно, что число является простым или четным, если и только если оно не является простым ине является четным.
(максимальное количество баллов - 6)
Задание №5. Определите, какие из приведенных высказываний логически следуют из высказывания «5 больше 3»:
а) 5 больше 3 или 3 больше 5.
б) Если 5 меньше 3, то 5 больше 3.
в) Если Париж расположен на Темзе, то 5 больше 3.
г) Неверно, что 5 больше 3 и вместе с тем 5 равно 3.
(максимальное количество баллов - 4)
Тема 4 (продолжение)
Информационный материал
Сложное высказывание будем назвать тождественно истинным или тавтологией, если оно принимает значение истины для всех наборов значений входящих в него простых высказываний.
Два сложных высказывания будем называть равносильными, если их значения совпадают при одних и тех же наборах значений входящих в них простых высказываний.
Доказательство приведенных ниже основных равносильностей алгебры высказываний выполняется при помощи составления таблиц истинности.
1. Закон тождества: 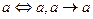 ;
;
2. Закон непротиворечия: 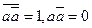 ;
;
3. Закон исключенного третьего: 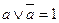 ;
;
4. Закон двойного отрицания: 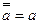 ;
;
5. Законы ассоциативности: 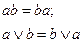 ;
;
6. Законы коммутативности: 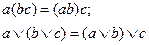 ;
;
7. Законы дистрибутивности: 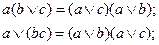
8. Законы поглощения: 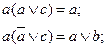
9. Законы де Моргана: 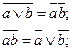
10. Связь конъюнкции, дизъюнкции, импликации и отрицания: 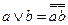 ;
;
11. 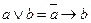 :
:
12. 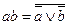 ;
;
13. 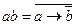 ;
;
14. 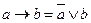 ;
;
15. 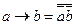 ;
;
16. Модусы (разновидности схемы утверждений): 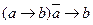 -утверждающий модус;
-утверждающий модус;
17. 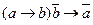 - отрицающий модус;
- отрицающий модус;
18. Отрицающе-утверждающий модус: 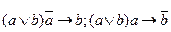 ;
;
19. Законы транзитивности: 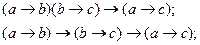
20. Законы контрапозиции: 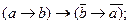
21. 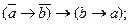
22. 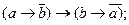
23. 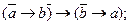
24. 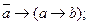
25. 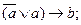
26. Законы косвенного доказательства: 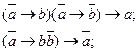
27. Законы Клавия: 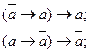
В качестве примера докажем, что, например, формулы и являются тождественно истинными (тавтологиями), построив для их левых и правых частей таблицы истинности и используя табличные определения основных логических операций
1. 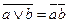
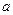 | 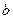 | 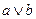 | 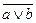 | 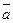 | 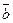 | 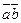 |
В четвертом и седьмом столбцах полученной таблицы содержаться истинностные значения, соответствующие левой и правой частям рассматриваемой формулы, и принимаемые этими выражениями значения одинаковы для всех наборов простых переменных, входящих в состав сложного высказывания. Значит, данная формула является тавтологией.
2. 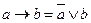
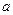 | 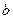 | 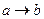 | 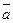 | 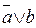 |
В третьем и пятом столбцах полученной таблицы содержатся истинностные значения, соответствующие левой и правой частям рассматриваемой формулы, и принимаемые этими выражениями значения одинаковы для всех наборов простых переменных, входящих в состав сложного высказывания. Значит, данная формула также является тавтологией.
Пример:
