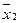| Обозначение функции и выражение через операции И, ИЛИ, НЕ | х1 | | | | | Название | Специальное обозначение | Чтение |
| х2 | | | | |
| f0 = 0 | | | | | | Константа «0» | | Всегда «0» |
| f1 = х1х2 | | | | | Конъюнкция | х1х2 | х1 и х2 |
f2 = 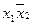 | | | | | Запрет по х2 | | Неверно, что если х1, то х2 |
| f3 = х1 | | | | | Переменная х1 | х1 | |
f4 = 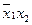 | | | | | Запрет по х1 | | Неверно, что если х2, то х1 |
| f5 = х2 | | | | | Переменная х2 | х2 | |
f6 = 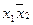 Ú Ú 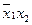 | | | | | Сложение по модулю 2 | х1Åх2 | х1 неравнозначно х2 |
| f7 = х1Úх2 | | | | | Дизъюнкция | х1Úх2 | х1 или х2 |
f8 = 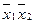 | | | | | Функция (стрелка) Пирса | x1¯x2 | Ни х1, ни х2 |
f9 = 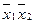 Ú Ú 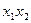 | | | | | Эквивалентность | x1«x2 | х1 равнозначно х2 |
f10 = 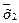 | | | | | Инверсия х2 | 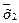 | Не х2 |
f11 = 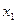 Ú Ú 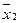 | | | | | Импликация | x2®x1 | Если х2, то х1 |
f12 = 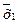 | | | | | Инверсия х1 | 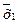 | Не х1 |
f13 = 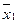 Ú Ú 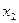 | | | | | Импликация | x1®x2 | Если х1, то х2 |
f14 = 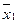 Ú Ú 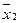 | | | | | Функция (штрих) Шеффера | x1/x2 | Неверно, что х1 и х2 |
| f15 = 1 | | | | | Константа «1» | | Всегда «1» |
Наши рекомендации
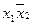
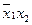
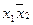 Ú
Ú 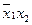
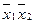
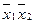 Ú
Ú 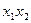
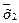
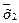
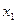 Ú
Ú 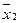
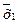
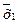
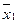 Ú
Ú 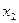
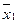 Ú
Ú