Определение 1. Пусть и произвольные множества. Соответствием называется тройка множеств 1 страница

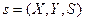, если 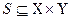. (5.1)

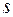При этом множество называется областью отправления соответствия , - областью прибытия этого соответствия, а 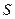- его законом или графиком.

С понятием соответствия также связывают следующие четыре множества:

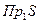- область определения соответствия 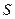(т.е проекция на первую координату от ) ;

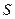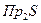- область значений соответствия ;

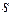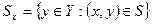- образ ;

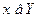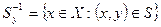- прообраз .

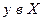Из определения всех этих множеств вытекают следующие отношения между ними:

.

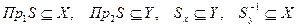Если пара 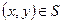, то говорят, что элементу 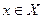соответствует элемент 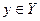, и, наоборот, когда 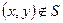, то говорят, что элементу 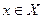не соответствует 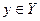. Поэтому образ 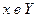есть множество 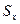, составленное из всех тех и только тех элементов множества , которые соответствуют элементу 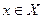, а прообраз 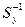содержит все те и только те элементы из , которым соответствует элемент .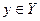

Выделяют следующие виды соответствий, вытекающие из различных соотношений между связанными с ним множествами.

Определение 1’. Соответствие 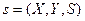называется:

1) отображением (или всюду определенным соответствием), если его области отправления и определения совпадают, т.е. ;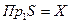

2) сюръекцией (или сюръективным соответствием), если совпадают его области прибытия и значений, т.е. ;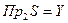

3) функцией (или однозначным соответствием), если образ любого элемента из множества содержит не более одного элемента, т.е. 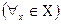[число элементов в 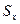не более 1];

4) инъекцией (или инъективным соответствием), если прообраз любого элемента из множества содержит не более одного элемента, т.е. 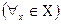[число элементов в 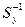не более 1];

5) биекцией (или взаимно однозначным соответствием), если оно одновременно является отображением, сюръекцией, функцией и инъекцией.

Таким образом, через соответствие как наиболее общее понятие только что формально определены новые математические объекты: отображение, сюръекция, функция, инъекция и биекция.

Следует отметить, что определение функции здесь значительно шире определения тех функций, которые рассматривались в школьном курсе математики. Там рассматривался частный случай функций, а именно действительных функций действительной переменной. Характерной особенностью таких соответствий является то, что их области отправления и прибытия представлены множеством действительных чисел, т.е. 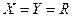. При графическом способе задания закона множества и представляются координатными числовыми осями и соответственно, а кривая графика функции состоит из точек множества .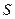

Проекция этой кривой на ось 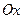(иначе говоря, 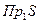) есть интервал 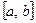, который в данном случае является областью определения, а проекция на ось 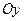( 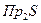) есть отрезок 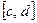– область значений этой функции. Заданный здесь закон 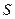определяет именно функцию (однозначное соответствие, в котором каждому соответствует не более одного ), т.е. кривую, которую любая вертикальная прямая пересекает не более чем в одной точке. Данная функция не является инъекцией, т.к. существует такое значение функции 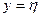, которое соответствует разным значениям переменной , т.е. прямая 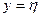(рис. 5.1) пересечет кривую 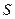более чем в одной точке.

На рис. 5.2 приведена кривая, которая является инъекцией (ни одна горизонтальная прямая не пересечет эту кривую более чем в одной точке), но не функцией (найдется такая вертикальная прямая 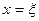, которая пересечет график 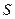более чем в одной точке).

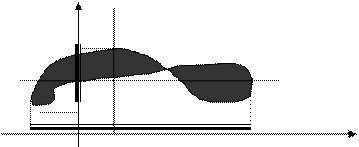
На рис. 5.3 закон соответствия 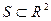задается областью (затемненная часть вещественной плоскости), не являющейся кривой. Такой график илююстрирует общий случай соответствия, которое не является ни функцией, ни инъекцией. Для него найдутся как вертикальные, так и горизонтальные прямые, которые пересекут область 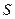более чем в двух точках (рис. 5.3).

Пример 5.1.Рассмотрим соответствие, определяющее, к какому времени года относится данный месяц.

X={январь, февраль, март, апрель, май, июнь, июль, август, сентябрь, октябрь, ноябрь, декабрь};

Y={зима, весна, лето, осень};

S={(январь, зима), (февраль, зима), (март, весна), (апрель, весна), (май, весна), (июнь, лето), (июль, лето), (август, лето), (сентябрь, осень), (октябрь, осень), (ноябрь осень), (декабрь, зима )}.

Очевидно, что данное соответствие является отображением, сюръективно, функционально и не является инъекцией.

Y

y d

d

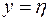
c c

a Ob x a O b x

Рис. 5.1. Функция Рис. 5.2. Инъекция

Y

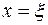
d

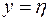
c

a O b x

Рис. 5.3. Общий случай соответствия

Для любого соответствия 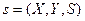всегда можно получить обратное соответствие 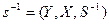. Для этого области отправления и прибытия следует поменять местами, а закон исходного соответствия возвести в степень –1. При этом 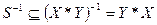. Из данных преобразований следует, что обратным соответствием от обратного соответствия будет исходное соответствие, т.е. .

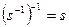Итак, любое соответствие имеет обратное. Однако не любая функция будет иметь обратную функцию. Функция будет иметь обратную только тогда, когда она одновременно и инъекция. При возведении закона 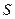в степень –1 свойства инъективности и однозначности взаимно заменяются. Поэтому для любой функции обратным соответствием будет инъекция и, обратно, обратным соответствием для любой инъекции будет функция.

Из правила преобразования соответствия в обратное также следует, что для любой сюръекции обратным соответствием будет отображение, и, обратно, обратным соответствием для любого отображения будет сюръекция.

Тогда обратным соответствием для биекции будет также биекция. Следовательно, для любой биекции существует обратная. Биекция также означает, что задана всюду определенная ( 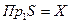) функция, для которой существует обратная всюду определенная функция.

Последовательное применение двух соответствий дает новое соответствие, которое называют композицией соответствий. Пусть имеются два соответствия 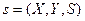и 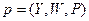, т.е. такие, что область прибытия первого соответствия совпадает с областью отправления второго. Тогда можно осуществить операцию композиции первого соответствия на второе . В результате получится новое соответствие

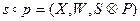, (5.2)

где

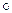- знак операции композиции;

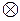- знак операции умножения двух двоичных матриц;

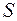- закон соответствия 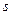, заданный двоичной матрицей*;

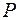- закон соответствия , заданный двоичной матрицей.

Это новое соответствие будет устанавливать связь уже между множествами и 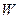. Например, если 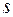- соответствие, определяющее распределение водителей по автобусам , а - соответствие, определяющее распределение автобусов по маршрутам 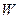, то соответствие 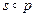определит распределение водителей по маршрутам .

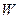Пример 5.2. Рассмотрим соответствие p между временем года и характеристикой погоды, качественно выражающей температуру в умеренных широтах.

Y={зима, весна, лето, осень}; W={тепло, холодно, неопределенно}; P={(зима, холодно), (весна, неопределенно), (лето, тепло), (осень, неопределенно)}.

Очевидно, что соответствие из примера 5.1 совместно с данным соответствием образует композицию, позволяющую определить характеристику месяца.

Вопросы для самоконтроля

1. Определите свойства и тип соответствия, которое задается списком дат знаменательных событий.

2. Будет ли соответствие, которое задает шахматная позиция (между - шахматными фигурами и - полями шахматной доски), функцией?

3. Определите области определения и значений для функции

.

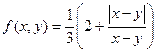5.1.2. Логические функции

Понятие функции в самом широком смысле уже дано в п. 5.1.1. Рассматриваемые в школьном курсе алгебры, а затем и в высшей математике действительные функции действительных переменных, суть частные случаи функциональных соответствий. Называются они так потому, что их областью отправления всегда является множество 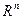( здесь 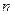– число переменных, от которых зависит функция; 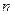=1, 2, …), а областью прибытия – множество 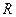действительных чисел.

Ниже рассмотрим случаи, когда множества, между которыми установлены функциональные соответствия, состоят из элементов, в общем случае не связанных с какими-нибудь числами. Такие соответствия получили название логических функций.

При изучении логических функций будем полагать, что их области отправления и прибытия суть абстрактные множества. При этом нас не будет интересовать конкретное содержание этих множеств – физическая природа их элементов. Чтобы различать такие элементы между собой, припишем каждому из них свой символ (или номер). Тогда область отправления логической функции будет представлена алфавитом, содержащим все эти символы, а некоторый иной символ, не принадлежащий данному алфавиту, будет называться логической переменной, если его можно заменять некоторыми из символов области отправления. Каждому из таких символов однозначным образом по заданному закону поставлен в соответствие единственный символ из области прибытия, а вся их совокупность образует область определения логической функции.

В самом общем случае алфавиты логических переменных, от которых зависит логическая функция, могут не совпадать. Тогда областью отправления будет являться прямое произведение этих алфавитов, а областью прибытия – какой-либо свой алфавит, который, в частности, может и совпасть с областью изменения одной из переменных. Когда алфавиты функций и переменных совпадают, над логическими функциями становится возможной операция композиции (операция «функция от функции»), с помощью которой из ограниченного набора простейших (базовых) логических функций можно получить все остальные логические функции.

Определение 2. Логическая функция от переменных ( 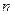=0, 1, 2, …) называется -местным предикатом, а ее переменные называются вхождениями. Нульместный предикат ( 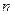=0) называют высказыванием; одноместный предикат

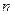( = 1) называют признаком или свойством; 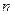- местный предикат, имеющий не менее двух вхождений ( 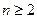), называют отношением.

Изучение логических функций начнем с простейших: свойства (признаки), бинарные отношения, булевы функции. Это и будут те самые базовые логические функции, из которых с помощью операции композиции можно получить и все остальные.

Вопросы для самоконтроля

1. Назовите основные отличия логических функций от основных элементарных функций, изучаемых в школе.

2. Приведите примеры логических переменных.

5.1.3. Признаки

Признак (свойство) - это функциональное соответствие вида

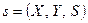, где 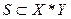. (5.3)

Рассмотренный пример 5.1 как раз определяет свойства, принадлежность какого-либо месяца к определенному времени года может рассматриваться как его (месяца) свойство.

Заданная таким образом тройка множеств 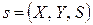, где 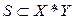, определяет некоторое соответствие между названиями месяцев и названиями времени года. Данное соответствие будет функцией, поскольку каждый из месяцев относится только к одному времени года. Тем самым задана логическая функция одной переменной (или свойство) вида у = SEASON(x), определяющая время года, соответствующее месяцу. Например, с учетом закона соответствия

SEASON(январь)= SEASON(февраль)= SEASON(декабрь)=зима;

SEASON(март)= SEASON(апрель)= SEASON(май)=весна;

SEASON(июнь)= SEASON(июль)= SEASON(август)=лето;

SEASON(сентябрь)= SEASON(октябрь)= SEASON(ноябрь)=осень.

Данная функция не является инъекцией, т.к. здесь не все прообразы имеют не более одного элемента. В частности, 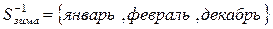содержит три элемента.

Данная логическая функция разбивает множество месяцев на четыре множества. Множества {январь, февраль, декабрь} зимних, {март, апрель, май} весенних, {июнь, июль, август} летних и {сентябрь, октябрь, ноябрь} осенних месяцев попарно не пересекаются, а их объединение равно - области определения этой логической функции, т.е.

{январь, февраль, декабрь} 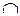{март, апрель, май} 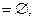{январь, февраль, декабрь} 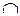{июнь, июль, август} 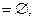{январь, февраль, декабрь} 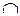{сентябрь, октябрь, ноябрь} 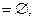{март, апрель, май} 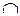{июнь, июль, август}, {март, апрель, май} 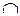{сентябрь, октябрь, ноябрь}, {июнь, июль, август} {сентябрь, октябрь, ноябрь} и {январь, февраль, декабрь} {март, апрель, май} {июнь, июль, август} {сентябрь, октябрь, ноябрь} .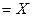

Следовательно, данная функция - это разбиение. И для любой другой логической функции это также справедливо.

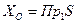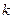Замечание 1. Всякая логическая функция задает разбиение своей области определения на попарно непересекающиеся подмножества, где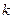 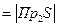- число элементов в ее области значений. Это следует из того, что, во-первых, объединение всех прообразов всегда будет являться областью значений в любом соответствии, а, во-вторых, условие того, что прообразы функционального соответствия попарно не пересекаются, вытекает из свойства однозначности.

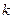Замечание 2. Справедливо и обратное. Если задано разбиение некоторого множества на попарно непересекающиеся классы, то это разбиение задает закон соответствия между множествами и , где - множество номеров классов разбиения, который является логической функцией с областями отправления и прибытия.

Замечание 3. Если логическая функция всюду определена, то замечание 1 справедливо и для ее области отправления , т.к. последняя в этом случае совпадает с ее областью определения 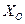. В противном случае (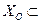 ) область отправления разобьется функцией на 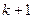частей, т.е. область будет включать в себя дополнительно еще одно подмножество 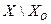, которое называют областью неопределенности. Например, если в законе соответствия исключить хотя бы одну пару, допустим пару (июнь, лето), то информация о том, к какому времени года относится июнь, будет утрачена и элемент июнь попадет в область неопределенности, т.е. при значении x=июнь полученная функция будет не определена.

Замечание 4. При замене вхождения в свойстве (одноместном предикате) конкретным значением получается нульместный предикат. Иначе говоря, свойство (признак) при конкретном значении переменной превращается в высказывание. Под высказыванием обычно понимают повествовательное предложение, которое может быть либо истинным, либо ложным. Например, SEASON(июнь)=лето, т.е. июнь - летний месяц есть истинное высказывание.