Вычислитель двоичных чисел
В вычислительных устройствах вычитание преобразуется в сложение путем суммирования дополнения вычитаемого Q с уменьшаемым P.
- 5
+ 2
Уменьшаемое P
Вычитаемое Q
Результат Σ со знаком «+»
P Q
0 1 1 1
0 1 0 1
Второе дополнение от Q образуется путем инвертирования каждого бита (1-ое дополнение) и его последующего сложения с «1».
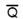1 0 1 0
+ 1
1 0 1 1 2-ое дополнение Q
0 1 1 1 P
+ 1 0 1 1 2-ое дополнение
10 0 1 0
Образующийся при сложении перенос не является результатом вычитания, но может быть использован для определения численных значений. Так как в двоично-кодированных числах положительный знак представлен через «0», то перенос в схеме должен отрицаться.
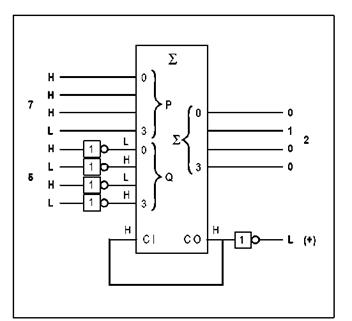
На рисунке 6.1.5.1 представлена схема вычитания, когда уменьшаемое больше вычитаемого.
Рисунок 6.1.5.1 Уменьшаемое > вычитаемое
Путем соединения CI и CO образуется 2-ое дополнение.
Если результат вычитания отрицательный, то на выходе требуется образование второго дополнения:
 |
5 Уменьшаемое P
- 7 Вычитаемое Q
- 
2 Результат Σ со знаком «-»
P 0 1 0 1
Q 0 1 1 1
1 0 0 0
+ 1
1 0 0 1 2-ое дополнение Q
0 1 0 1 P
+ 1 0 0 1 2-ое дополнение
01 1 1 0 2-ое дополнение результата Σ
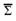0 0 0 1
+ 1
0 0 1 0
На рисунке 6.1.5.2 представлена схема вычитания, когда уменьшаемое меньше вычитаемого.
В схеме на рисунке 6.1.5.2 нет сложения «1», так как она должна появиться как на входе, так и на выходе.
Рисунок 6.1.5.2 Уменьшаемое < вычитаемое