Использование законов Кирхгофа для расчета электрических цепей
Пусть электрическая цепь представлена в виде схемы (рис.1.10)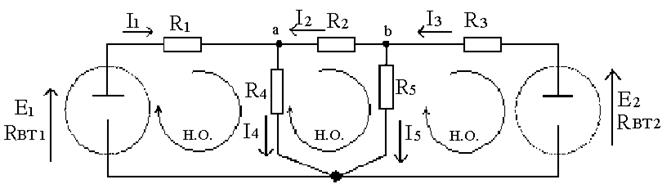 
Рис.1.10. Электрическая цепь постоянного тока
При заданных значениях ЭДС и сопротивлений, необходимо составить количество уравнений, равное количеству ветвей в цепи. Из всего количества уравнений n-1 уравнений составляются по первому закону Кирхгофа, где
n - количество узлов цепи. Остальные уравнения составляются по второму закону Кирхгофа.
Для рассматриваемой цепи количество ветвей равно 5, количество узлов равно 3. По первому закону Кирхгофа составим два уравнения, по второму закону Кирхгофа составим три уравнения.
Произвольно выбираем положительные направления токов ветвей I1, I2, I3, I4, I5, а также направления обходов независимых контуров.
Для узлов “a” и “b” составим уравнения по первому закону Кирхгофа:
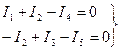(1.17а)
Для независимых контуров составим уравнения по второму закону Кирхгофа:
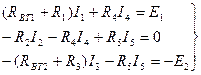(1.17б)
Решая систему линейных уравнений (1.17а) и (1.17б) с пятью неизвестными токами, определяем значения токов ветвей.
Целесообразно решать систему уравнений численными методами на ЭВМ с использованием матричной формы:
* 
= 
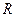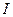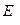, (1.18)
где 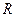- квадратная матрица 5х5 постоянных коэффициентов значений сопротивлений при токах цепи; 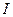- вектор столбец неизвестных токов ветвей, 
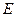- вектор столбец постоянных коэффициентов значений ЭДС цепи.
При отсутствии тех или иных токов и ЭДС, в каких либо уравнениях, задаются значениями «ноль» соответствующих элементов матриц. Решение системы (1.18) можно выполнить в компьютерной среде MATLAB:
= 
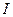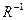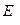* , (1.19а)
где 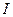- вектор столбец неизвестных токов ветвей, 
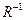- обратная квадратная матрица постоянных коэффициентов значений сопротивлений при токах цепи.
Систему (1.19а) представим в матричной форме:
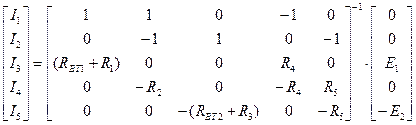(1.19б)
В среде MATLAB можно обратную матрицу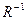 
представить в виде инверсии матрицы R:
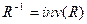. (1.20)
Тогда выражение (1.19а) будет иметь вид:
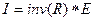, (1.21)
где E - вектор - cтолбец значений ЭДС цепи.
Введём в компьютер исходные данные системы (1.19б)
>> =[ 
; ; ( 
) 
; 
; 
]
>> = [ ; ; 
; ; 
]
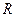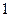
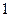
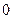
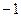
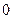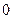
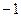
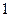
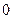
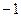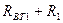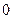
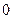
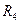
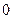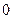
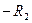
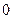
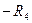
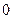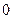
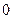
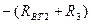
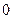
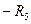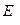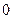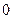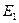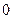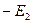и, записав выражение (1.21), получим численное решение неизвестных значений токов ветвей I1, I2, I3, I4, I5. При отрицательных значениях токов необходимо изменить их направления в ветвях.