Краткие методические указания к решению задачи 3
Все расчеты в задаче 1 проведены по индивидуальным значениям признаков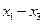 
. Первоначально в задаче 1 расчеты ведутся по всему информационному массиву (простая статистическая сводка). Затем в задаче 2 все расчеты также проводятся по индивидуальным данным, но они уже проранжированы и распределены по однородным группам в зависимости от численного значения признака, принятого за основание группировки (сложная статистическая сводка).
По условиям данной задачи требуется определить обобщающие статистические показатели на основе уже рассчитанных статистических характеристик. Последовательность ее решения следующая.
Во-первых, рассчитываются общие средние величины признаков 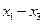из их групповых значений:
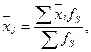
где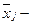 
общая средняя величина 
го признака; 
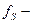средняя величина го признака в 
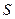группе, или веса, или частоты.
Во-вторых, рассчитывается дисперсия средняя из групповых:
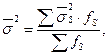
где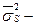 
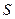дисперсия го признака в группе.
В-третьих, определяется общая дисперсия:
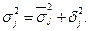
В данном случае используется взаимосвязь, соответствующая между тремя видами дисперсий, или правило сложения дисперсий, согласно которому общая дисперсия равна сумме средней из внутригрупповых и межгрупповых дисперсий. Зная любые два вида дисперсии, можно определить или проверить правильность расчета третьего вида.
В-пятых, рассчитываются коэффициент детерминации и эмпирическое корреляционное отношение:
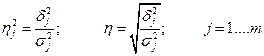
где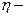 
эмпирическое корреляционное отношение. Оно изменяется в пределах от 0 до 1. Чем ближе к 1 значение эмпирического корреляционного отношения, тем больше оснований для утверждения о наличии значимой статистической связи между изучаемыми признаками.
Расчеты названных общих статистических характеристик проводится отдельно по каждому признаку. Ниже приводится для иллюстрации последовательность расчета и результаты решения задачи 3. Для признака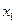 
имеем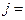 
1 (табл. 13, 14, 15). Все данные в нижеперечисленных таблицах распределены на 6 групп. Для заполнения таблицы 13 используются данные из табл.9 и 7.
Таблица 13
Расчет общей средней величины признака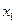
Из его средних групповых значений
| Номер группы |  |  |  |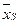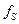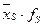
| 3946,67 | 11840,00 | ||
| 5250,00 | 26250,00 | ||
| 6845,00 | 47215,00 | ||
| 8499,00 | 84990,00 | ||
| 9826,00 | 29480,00 | ||
| 11750,00 | 23500,00 | ||
| Итого | - | 223975,00 |
По данным табл.13 получаем значение средней величины :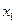
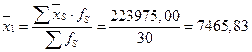руб.
Для заполнения табл.14 используются групповые дисперсии признаков, представленные в табл.10. Для признака 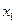используются данные графы 2 табл.10 с дисперсиями 
.
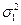Таблица 14