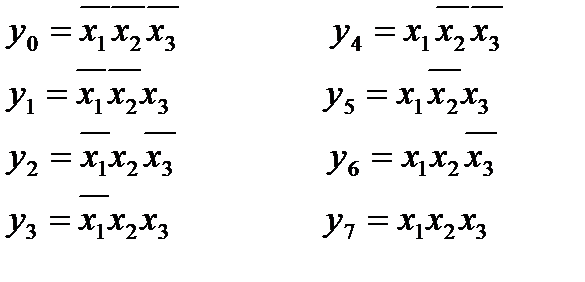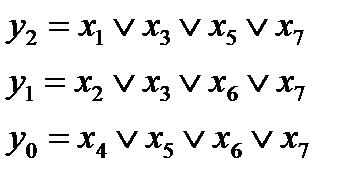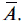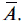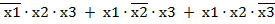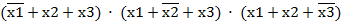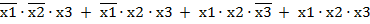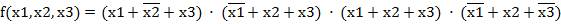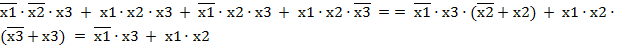Для составления схемы электрической функциональной необходимо, прежде всего, решить задачу написания системы собственных функций или фуункции, отражающей логику работы этой схемы и имеющей однозначное решение. Для этого составляют таблицу истинности, в которой задается значение функции в зависимости от комбинации входных сигналов.
Синтез состоит в построении функциональной электрической схемы по минимизированной функции (в базисе {И, НЕ и ИЛИ}, {И-НЕ} или {ИЛИ-НЕ}). Для выполнения синтеза необходимо:
- по таблично-заданной функции, описывающей работу заданной схемы, составить СДНФ
- минимизировать СДНФ с помощью законов и аксиом алгебры логики либо диаграмм Вейча;
- начертить функциональную электрическую схему по минимизированной функции
«Анализ и синтез дешифратора и шифратора»
Дешифраторы (ДШ) — это комбинационные схемы с n входами и m = 2n выходами. Единичный сигнал, формирующийся на одном из m выходов, однозначно соответствует комбинации входных сигналов. Например, разработка структуры ДШ для n=3 согласно методике, изложенной в описании лабораторной работы №1 , позволяет получить 8 (по количеству функций-выходных сигналов) таблиц истинности (табл. 2.1) и логические зависимости.
Таблица 1.1
Таблица истинности дешифратора
| Входы | Выходы |
| x1 | x2 | x3 | у0 | y1 | ... | y5 | ... | y7 |
| | | | | | ... | | ... | |
Дешифраторы широко используются в ЭВМ для выбора информации по определенному адресу, для расшифровки кода операции и др.
Логические зависимости дешифратора:
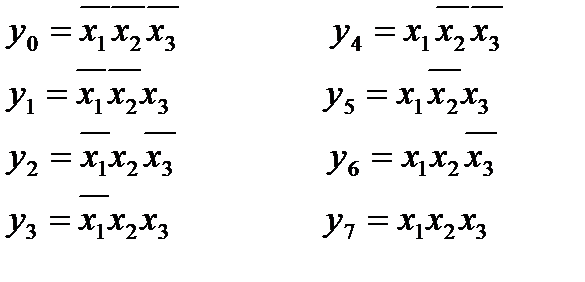
На рис. 2.1 представлены структурная схема ДШ, построенная в базисе (И-НЕ, И), и условное ее обозначение на принципиальных электрических схемах ЭВМ. Кружочки у линий, выходящих из логических элементов, указывают на инверсию функций, реализуемых элементами.
Рис. 2.1. Структурная схема дешифратора (а) и обозначение дешифратора на принципиальных электрических схемах (б)
Шифратор (ШР) решает задачу, обратную схемам ДШ, т. е. по номеру входного сигнала формирует однозначную комбинацию выходных сигналов. Номер входного сигнала определяется присутствием логической единицы на соответствующем входе (только одном). Соответствие комбинации выходных сигналов номеру входного можно задать соответствующей таблицей. Для 4 входных сигналов она может выглядеть следующим образом - таблица 2.2
Таблица 2.2
| Входы | Выходы |
| x1 | x2 | x3 | x4 | y1 | y2 |
| | | | | | |
Состояния входов табл. 1.2 содержат только по одному единичному элементу. Другие произвольные комбинации входов недопустимы.
Данная таблица, по существу, представляет из себя 2 неполные таблицы истинности для двух выходных сигналов — y1 и y2. Полные таблицы истинности представлены в таблице 1.3.
Таблица 1.3
| Входы | Выходы |
| x1 | x2 | x3 | x4 | y1 | y2 |
| | | | | 0* | 0* |
| | | | | | |
| | | | | | |
| | | | | 0* | 1* |
| | | | | | |
| | | | | 1* | 1* |
| | | | | 1* | 0* |
| | | | | 1* | 1* |
| | | | | | |
| | | | | 1* | 1* |
| | | | | 1* | 1* |
| | | | | 1* | 1* |
| | | | | 1* | 1* |
| | | | | 1* | 1* |
| | | | | 1* | 1* |
| | | | | 1* | 1* |
Значения выходных сигналов со знаком * означают, что они не были заданы в исходной таблице 2.2 и могут быть заданы произвольно. В данном случае это доопределение делалось из условия минимизации логических схем, реализующих таблицы истинности, что иллюстрируется диаграммой Вейча для функции y1.- Таблица 2.4
Таблица 1.4
Диаграмма Вейча функцииу
1 | |  |  |  | |
 | 1* | 1* | 1* | |  |
| 1* | 1* | 1* | 1* |  |
 | 1* | 1* | 1* | |
| | 0* | | 0* |  |
| |  |  | |
В результате получается минимизированное логическое выражение:
y1 = x1 v x2
Аналогично для функции y2:
y2 = x1 v x3
Пример построения ШР для 7 входных сигналов иллюстрируется неполными таблицами истинности для трех выходных сигналов-логических функций (табл. 1.5) и схемами на рис. 1.2.
Таблица 1.5
Таблица истинности шифратора | Входы | Выходы |
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | y1 | y2 | y3 |
| | | | | | | | | | |
Логические зависимости шифратора:
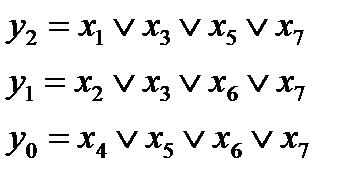
Рис. 2.2. Структурная схема шифратора (а) и обозначение шифратора на принципиальных электрических схемах (б)
| Синякина Г.Е. МММММММММММММММммухамедшиной. |
| Монтаж, наладка и эксплуатация САУ |
15. Логические переменные алгебры логики. Их значения. Информация (данные, машинные команды и т. д.) в компьютере представлена в двоичной системе счисления, в которой используется две цифры – 0 и 1. Электрический сигнал, проходящий по электронным схемам и соединительным проводникам (шинам) компьютера, может принимать значения 1 (высокий уровень электрического напряжения) и 0 (низкий уровень электрического напряжения) и рассматривается как импульсный сигнал, который математически может быть описан в виде двоичной переменной, принимающей также значения 0 или 1. Для решения различных логических задач, например, связанных с анализом и синтезом цифровых схем и электронных блоков компьютера, широко используются логические функции и логические операции с двоичными переменными, которые называются также логическими переменными.
Логические переменные изучаются в специальном разделе математики, который носит название алгебры логики (высказываний), или булевой алгебры. Булева алгебра названа по имени английского математика Джорджа Буля (1815–1864), внесшего значительный вклад в разработку алгебры логики. Предметом изучения алгебры логики являются высказывания, при этом анализу подвергается истинность или ложность высказываний, а не их смысловое содержание. Простые высказывания в алгебре логики обозначаются заглавными латинскими буквами: А, В, С, D,… и т. д. Составные высказывания на естественном языке образуются с помощью союзов. В алгебре логики эти союзы заменяются логическими операциями. В соответствии с алгеброй логики любое составное высказывание можно рассматривать как логическую функцию F(А, В, С, …), аргументами которой являются логические переменные А, В, С… (простые высказывания). Логические функции и логические переменные (аргументы) принимают только два значения: «истина», которая обозначается логической единицей – 1 и «ложь», обозначаемая логическим нулем – 0. Логическую функцию называют также предикатом.
Действия, совершаемые над логическими переменными для получения определенных логических функций, называются логическими операциями. В алгебре логики используются следующие логические операции.
1. Логическая операция ИНВЕРСИЯ (отрицание). В естественных языках соответствует словам неверно, ложь или частице не, в языках программирования обозначается Not, в алгебре логики обозначается
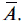
Инверсия каждому простому высказыванию ставит в соответствие составное высказывание, заключающееся в том, что исходное высказывание отрицается.
Математическая запись данной операции для логической переменной А будет иметь вид:
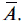
2. Логическая операция КОНЪЮНКЦИЯ (логическое умножение). В естественных языках соответствует союзу и, в языках программирования обозначается And, в алгебре логики обозначается & .
Конъюнкция каждым простым высказываниям ставит в соответствие составное высказывание, являющееся только тогда истинным, когда являются истинными простые высказывания, образующие составное высказывание.
Математическая запись данной операции для логических переменных Д В, С, … будет иметь вид:
F = A & B & C & …
3. Логическая операция ДИЗЪЮНКЦИЯ (логическое сложение). В естественных языках соответствует союзу или, в языках программирования обозначается Or, в алгебре логики обозначается V.
Дизъюнкция каждым простым высказываниям ставит в соответствие составное высказывание, являющееся только тогда истинным, когда хотя бы одно из образующих его высказываний является истинным.
Математическая запись данной операции для логических переменных A, В, С, … будет иметь вид:
F = AvBvC…
4. Логическая операция ИМПЛИКАЦИЯ (логическое следование). В естественных языках соответствует обороту речи, если…, то …, в языках программирования обозначается If, в алгебре логики обозначается ?.
Импликация каждым простым высказываниям ставит в соответствие составное высказывание, являющееся ложным тогда и только тогда, когда первое высказывание истинно, а второе высказывание ложно.
Математическая запись данной операции для двух логических переменных А и В будет иметь вид:
F = A=>B.
5. Логическая операция ЭКВИВАЛЕНЦИЯ (логическая равнозначность). В естественных языках соответствует обороту речи тогда и только тогда, в алгебре логики обозначается =>.
Эквиваленция каждым простым высказываниям ставит в соответствие составное высказывание, являющееся истинным тогда и только тогда, когда все простые высказывания, образующие составное высказывание, одновременно истинны или одновременно ложны.
Математическая запись данной операции для логических переменных A, В, С… будет иметь вид:
F = A=>B=>C=>…
| Синякина Г.Е. МММММММММММММММммухамедшиной. |
| Монтаж, наладка и эксплуатация САУ |
16. СКНФ, СДНФ, Правила минимизации. Любая логическая схема без памяти полностью описывается таблицей истинности. Эта таблица является исходной информацией для синтеза схемы на основе логических элементов «И», «ИЛИ», «НЕ». Для разработки требуемого цифрового устройства сначала на основе таблицы истинности записывают его логическое выражение. Затем с целью упрощения цифрового устройства минимизируют его логическое выражение и далее разрабатывают схему, реализующую полученное логическое выражение. Логические выражения можно получить двумя способами:
на основе совершенной дизъюнктивной нормальной формы (СДНФ);
на основе совершенной конъюнктивной нормальной формы (СКНФ).
Совершенная дизъюнктивная нормальная форма (СДНФ)
Функция представляется суммой групп. Каждая группа состоит из произведения, в которую входят все переменные.
Например:
f(x1,x2,x3) = 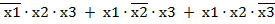
Совершенная конъюнктивная нормальная форма (СКНФ)
Функция представляется произведением групп. Каждая группа состоит из суммы, в которую входят все переменные.
Например:
f(x1,x2,x3)= 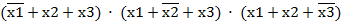
Если схема имеет несколько выходов, то каждый выход описывается своей функцией. Такая система функций называется системой собственных функций. СДНФ составляется на основе таблицы истинности по следующему правилу: для каждого набора переменных, при котором функция равна 1, записывается произведение, в котором с отрицанием берутся переменные, имеющие значение «0».
Пример:
Таблица 2.1 – Заданная таблица истинности
СДНФ: y = f(x1,x2,x3)= 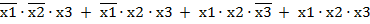
СКНФ составляется на основе таблицы истинности по правилу: для каждого набора переменных, при котором функция равна 0, записывается сумма, в которой с отрицанием берутся переменные, имеющие значение 1.
Таблица 2.2 – Заданная таблица истинности
СКНФ: y = 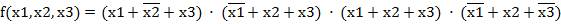
На основе полученных выражений можно составить схему устройства, реализующего заданную функцию. Схема устройства, полученная на основе СДНФ, изображена на рисунке 2.1, а на основе СКНФ на рисунке 2.2.

Рисунок 2.1 — Схема устройства, полученная на основе СДНФ
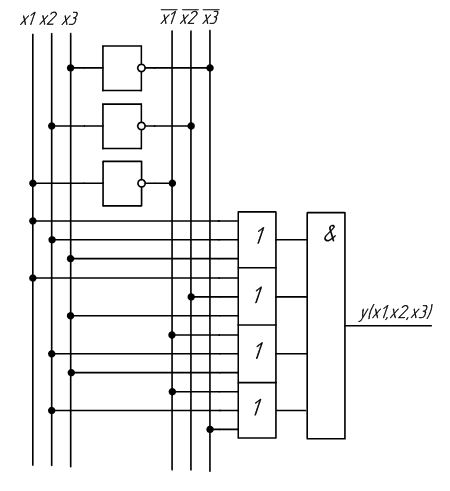
Рисунок 2.2 — Схема устройства, полученная на основе СКНФ
С целью упрощения цифрового устройства применяют минимизацию функций. Используя законы алгебры логики можно упростить исходную функцию.
y(x1,x2,x3)= 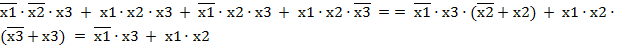
На основе полученного выражения составим новую схему устройства (рисунок 2.3).
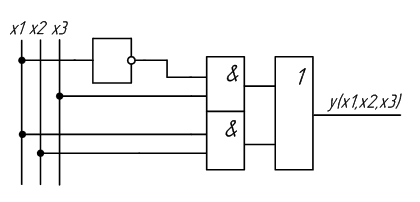
Рисунок 2.3 – Схема устройства, полученная после минимизации логической функции
Литература
1.
| Синякина Г.Е. МММММММММММММММммухамедшиной. |
| Монтаж, наладка и эксплуатация САУ |
http://www.labfor.ru/guidance/digital-leso2/2
2. http://www.nnre.ru/kompyutery_i_internet/informatika_apparatnye_sredstva_personalnogo_kompyutera/p5.php
3. http://umk.portal.kemsu.ru/uch-mathematics/papers/posobie/r3-2.htm
4. http://dic.academic.ru/dic.nsf/ruwiki/659622