Определение 1. Пусть и произвольные множества. Соответствием называется тройка множеств 3 страница

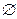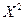Замечание 2.Средиотношений особо следует выделить отношения с областями истинности и . В алгебре бинарных отношений они играют роль логических констант ( 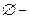константа «ложь», 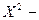константа «истина»). Отношение 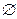здесь является единичным (нейтральным) элементом для операции объединения, т.к. для любого отношения выполняются равенства , а отношение 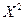является таким элементом для операции совмещения ( 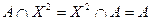). Отношение 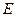(«быть равным») в этой алгебре является единицей операции композиции, т.е. для любого отношения имеют место соотношения .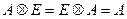

Таким образом, подобно действительным функциям, отношения можно задавать таблично (двоичными матрицами), графически (в виде графов) и аналитически (в виде формул, с использованием алгебраических операций).

Вопросы для самоконтроля

1. Отношения, рассмотренные в примерах 5.3 – 5.7, выразите через отношение 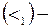«быть меньше ровно на единицу».

2. На множестве 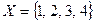задайте следующие отношения в виде двоичных матриц: а) «не равно», б) «быть кратным», в) «иметь в сумме не менее 2», г) «быть больше более чем на 3».

Свойства отношений

Данные свойства не то же самое, что свойства (признаки), рассмотренные в п.5.1.3. Последние это одноместные предикаты, которые определяют свойства предметов из области , а первые – свойство отношений между этими предметами. Кстати сказать, если не различать свойство предметов и свойство свойств тех же предметов, то можно придти к известному «парадоксу» Рассела.

Определение 10. Отношение , определенное в области 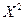, называется рефлексивным, если .

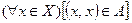Из данного определения следует, что двоичная матрица рефлексивного отношения имеет единичную диагональ, т.е. 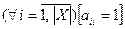или

, (5.12)

где 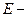отношение «равно».

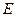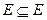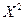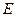
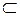
Тогда само отношение «равно» рефлексивно ( обладает свойством рефлексивности, т.к. ). Другие примеры рефлексивных отношений: (поскольку 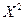); «быть подмножеством», т.к. любое множество является элементом самого себя ( 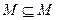); «меньше либо равно» (отношение 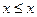выполняется для любого числа ); «не лучше», «не хуже» (никто не лучше и не хуже самого себя); «обладать тем же свойством, что и» (любой предмет обладает тем же свойством, которым он обладает)…

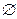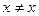Примеры нерефлексивных отношений: , «не равно», «меньше», «больше» (при любом неравенство невыполнимо, равно как и такие 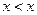, 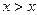), «умнее» (умнее самого себя быть невозможно).

Определение 11. Отношение , определенное в области 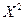, называется антирефлексивным, если ( ).

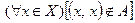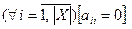Следовательно, двоичные матрицы антирефлексивных отношений имеют главную диагональ нулевую (состоящую из одних нулей). Тогда свойство антирефлексивности для некоторого отношения можно определить также соотношением

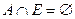. (5.13)

Вот примеры некоторых антирефлексивных отношений: 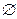, «не равно», «меньше», «больше», «умнее», «главнее», «быть отцом», «быть дедом» и т.д.

Однако отношения «быть довольным кем-либо» и «быть влюбленным в кого-либо» не будут ни антирефлесивными, ни рефлексивными. Главные диагонали их двоичных матриц содержат как нули, так и единицы (самодовольные и самовлюбленные на этих диагоналях отмечены единицами, а те, кто этим не грешит, - нулями).

Замечание 1.Из рефлексивности и антирефлексивностиследует, что одно и то же отношение не может быть одновременно и рефлексивным, и антирефлексивным, но существуют еще нерефлексивные отношения, которые не удовлетворяют ни одному из этих свойств. Поэтому данные свойства делят все множество отношений на три класса – рефлексивный, антирефлексивный и нерефлексивный.

Определение 12. Отношение , определенное в области 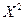, называется симметричным, если .

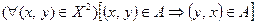Поскольку условие равносильно 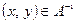, то из определения следует, что в симметричном отношении любой элемент из множества находится и в области 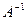, т.е.

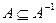. (5.14)

Теорема 1. Отношение симметрично тогда и только тогда, когда оно равно обратному ( ).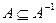

Доказательство. Необходимость. Пусть отношение симметрично, т.е. 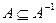. Осталось доказать, что и 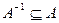. Пусть 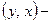произвольный элемент множества 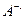, но это равносильно тому, что 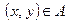, откуда по определению симметричности 12 следует, что и . Тогда по определению подмножества 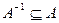, а т.к. еще и 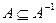, то по определению равных множеств .

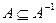Достаточность. Пусть , тогда из определения равных множеств следует, что и 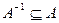, т.е. условие (5.14) выполнено, а отношение симметрично. Теорема доказана.

Следствие 1. Обратное отношение любого симметричного отношения то же самое отношение. Иначе говоря, возведение в степень –1 симметричных отношений является для них пустой операцией.

Следствие 2. Двоичная матрица симметричного отношения симметрична относительно главной диагонали, т.е. .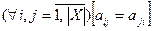

Примеры симметричных отношений: 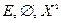, 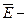«не равно» (если , то и 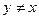), «быть коллегой» (если коллега , то и коллега ), «обладать тем же свойством, что и» (если обладает тем же свойством, что и , то и обладает тем же свойством, что и )…

Определение 13. Отношение 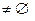, определенное в области 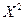, называется асимметричным, если 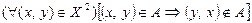т.е. 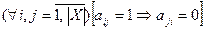, что соответствует асимметричной относительно главной диагонали двоичной матрице.

Из данного определения следует, что асимметричные отношения удовлетворяют соотношению

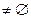
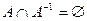. (5.15)

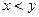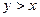Примеры асимметричных отношений: «меньше» (если , то будет больше , ), «быть сыном» (если является сыном , то 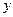уже не будет сыном ), «быть надежнее » (если надежнее , то надежнее уже быть не может)…

Теорема 2. Асимметричные отношения всегда антирефлексивны ( ).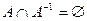

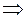
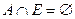Доказательство. Предположим противное. Пусть наше асимметричное отношение не антирефлексивно, т.е. найдется такой элемент , что пара . Однако эта пара не меняется при перестановке местами ее компонент. Поэтому она неизбежно попадет и в область 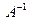, но тогда 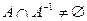, а это противоречит свойству асимметрии отношения и доказывает, что наше предположение не верно. Тогда верным является утверждение настоящей теоремы.

Определение 14. Отношение , заданное в области 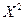, называется антисимметричным, если .

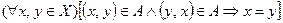Поскольку условие равносильно 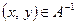, то из условия антисимметричности и определения операции пересечения следует, что 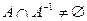и 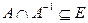, т.е.

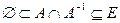. (5.16)

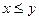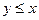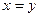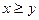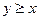Примеры антисимметричных отношений: «меньше либо равно» (если и , то ), «не меньше» (если и , то 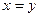), «быть не хуже» (если не хуже и не хуже , то и равнозначны), «быть не старше» (если не старше и не старше , то и одного возраста) и т.д.

Замечание 2.Симметричные отношения не могут быть асимметричными или антисимметричными, т.к. условия (5.14), (5.15) и (5.16) попарно не выполнимы в любом сочетании. Поэтому каждое из отношений может быть либо только симметричным, либо асимметричным, либо антисимметричным, либо вообще никаким, если для него не выполняется ни одно из этих условий. Такие отношения назовем несимметричными. В области истинности несимметричных отношений присутствуют одновременно симметричные, асимметричные и антисимметричные пары. Например, отношение «любить» явно несимметричное. Условие «если любит , то любит » выполняется, увы, не для всех пар. Бывает любовь и безответной, которую можно задать для несебялюбов условием «если любит , то не любит ». Ну а для «возлюбивших себя» безответная «любовь к ближнему» - это когда из того, что любит , а любит , следует, что и есть .

Определение 15. Отношение , заданное в области 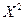, называется транзитивным, если .

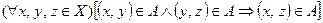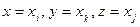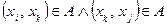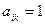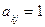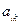
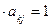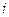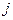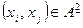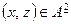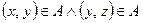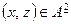Определим особенности двоичной матрицы для данного отношения. Пусть . Тогда из условия следует, что и . Поэтому , откуда согласно (5.11) имеем, что в -й строке -го столбца матрицы стоит единица, что равносильно условию или . Значит, условия и равнозначны и транзитивные (по определению транзитивности) отношения должны удовлетворять условию

,

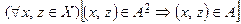которое по определению подмножества дает

. (5.17)

Теорема 3. Отношение транзитивно тогда и только тогда, когда оно равно своему транзитивному замыканию, т.е.

.

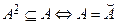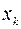
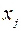
Доказательство. Необходимость. Поскольку

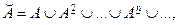
то 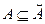. Осталось доказать, что если , то

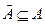. Рассмотрим геометрический смысл матриц

.

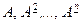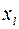
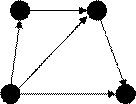
Матрица определяет дуги графа согласно

правилу: если 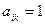, то из вершины 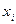графа в Рис. 5.5

вершину существует путь длиной в одну дугу.

По аналогичному правилу матрица определяет пути длиной в две дуги между вершинами данного графа, а матрица 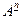- пути длиной в 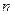дуг.

Условие (5.14) говорит о том, что если между вершинам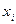и и 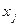имеется путь длины 2 (на рис. 5.5 этот путь представлен парой смежных дуг 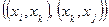, его также можно зафиксировать тройкой ( 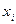, , 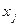) вершин, через которые он пролегает), то должна существовать и дуга ( , ).

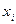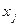Теперь рассмотрим произвольный путь ( 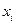, , 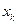, 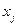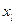) длины 3 в нашем графе (рис. 5.5). На основании условия (14) дуга ( 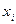, 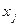) 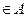, но тогда существует путь ( 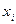, , 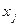) длины 2, т.е. ( 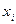, ) , а на основании (5.14) имеем, что ( 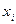, ) 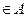. Следовательно, в транзитивном отношении .

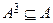Аналогично доказывается, что и 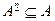, где 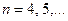. Но тогда 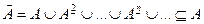и 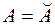. Необходимость доказана.

Достаточность. Пусть теперь 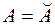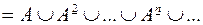. Но тогда , т.е. отношение транзитивно.

Замечание 3. Свойство транзитивности не зависит от других рассмотренных выше свойств отношений. Оно разбивает все отношения на два класса – транзитивные и не транзитивные.

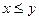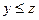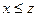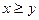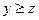Примеры транзитивных отношений: «меньше либо равно» (если и , то ), «не меньше» (если и , то 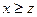), «быть не хуже» (если не хуже , а не хуже , то не хуже ), «быть братом» (если брат , а брат , то и брат ) и т.д.