Операция изменения кода числа называется его преобразованием. Интегральные микросхемы, выполняющие эти операции, называются преобразователями кодов. Интегральные микросхемы преобразователей кодов выпускаются только для наиболее распространённых операций таких как преобразователи двоичного кода в десятичный, двоично-десятичный, шестнадцатеричный, код Грея или обратных, указанным выше, преобразований.
По своей структуре преобразователи кодов являются дешифраторами, только они преобразуют двоичный код в сигналы не только на одном, но и на нескольких выходах.
В качестве примера рассмотрим преобразователь двоичного кода в код управления 7-сегментным цифровым индикатором. На рисунке 16,а приведена схема подключения индикатора. Индикатор представляет собой полупроводниковый прибор, в котором имеется восемь сегментов, выполненных из светодиодов. Включением и выключением отдельных сегментов можно получить светящееся изображение отдельных цифр или знаков.
Конфигурация и расположение сегментов индикатора показаны на рисунке 16,а. Каждой цифре соответствует свой набор включения определённых сегментов индикатора. Соответствующая таблица отображения цифр и десятичной разделительной точки приведена на рисунке 16,б.

Рисунок 16 Преобразователь двоичного кода в код 7 – сегментного индикатора:
а) — Схема подключения индикатора; б) — Таблица состояний.
По внутренней схеме включения индикаторы подразделяются на индикаторы с общим катодом и с общим анодом. Схемы обоих видов индикаторов приведены на рисунке 17,а и 17,б соответственно.
Существует широкая гамма различных модификаций семисегментных индикаторов. Они отличаются друг от друга размерами, цветом свечения, яркостью, расположением выводов.

Рисунок 17 Схемы индикаторов: а) — с общим катодом; б) — с общим анодом.
Для управления индикатором с общим катодом используется, например, дешифратор К514ИД1, а с общим катодом — К514ИД2. Используются микросхемы дешифраторов и других серий, например, 176ИД2, 176ИД3, 564ИД4, 564ИД5, К133ПП1 и др.
Шкальные индикаторы (светящиеся столбики) представляют собой линейку светодиодов с одним общим анодом или катодом. Они являются аналогами щитовых измерительных приборов и служат для отображения непрерывно изменяющейся информации.
Светящиеся шкалы могут быть установлены на приборном щитке автомобиля или самолёта для индикации уровня горючего в баке, скорости движения и других параметров. Удобна конструкция в виде расположенных рядом столбиков для индикации величин с целью их сравнения.
Преобразователи двоичного кода в код управления шкальным индикатором обеспечивают перемещение светящегося пятна, определяемое двоичным кодом на адресном входе.
Матричные индикаторы представляют собой наборы светодиодов, расположенных по строкам и столбцам. Наиболее распространённые матричные индикаторы имеют 5 столбцов и 7 строк (формат 5×7). Количество светодиодов таких индикаторов равно 35. Для управления матричными индикаторами выпускаются микросхемы, в которых положение светодиода задаётся номерами строки и столбца, причём не все комбинации используются. Такие преобразователи кодов называются неполными. К ним относятся, например, микросхемы К155ИД8 и К155ИД9.
| Синякина Г.Е. МММММММММММММММммухамедшиной. |
29. Духкаскадный дешифратор с прямоугольным матречным дешифратором на втором каскаде В прямоугольных дешифраторах n его входов разбиваются на две группы по n/2 переменных в каждой группе при четном n, при нечетном п группы должны содержать по (n+1)/2 и (п-1)/2 переменных (рисунок 18). Для каждой из двух групп строится линейный дешифратор. Эти дешифраторы составляют первую ступень дешифрации. Затем по матричной схеме с помощью элементов И на два входа каждая выходная шина одного дешифратора объединяется с каждой выходной шиной другого и таким образом получается вторая ступень дешифрации.

Рисунок 18. Двухкаскадный дешифратор с прямоугольным (матричным) дешифратором во втором каскаде
Делить разряды адреса между DС1 и DС2 нужно по возможности поровну: чем ближе прямоугольник второго каскада к квадрату, тем при том же числе выходных элементов И меньше сумма его строк и столбцов, т. е. меньше число выходов дешифраторов первого каскада. В качестве входа Е всего двухкаскадного дешифратора удобно использовать разрешающий вход одного из дешифраторов первого каскада. При этом запираются или все строки, или все столбцы.
Целесообразно сравнить три рассмотренных типа дешифраторов по величине задержки и аппаратурным затратам. Задержка минимальна для линейного дешифратора и в пределе может быть равна (2-3) т в зависимости от числа ступеней инверторов-усилителей. При включении линейных дешифраторов в несколько каскадов задержки всех каскадов складываются. Чем больше число выходов дешифратора, тем большая доля оборудования сосредоточена в элементах И самого последнего каскада. Число элементов предпоследнего каскада уже в несколько раз меньше, чем последнего, а предыдущих — тем более.
Число элементов И последнего каскада дешифратора любого типа всегда равно числу его выходов, поэтому в первом приближении аппаратурные затраты дешифраторов различных типов соотносятся как аппаратурные затраты их элементов И последнего каскада. Они и определяют основную разницу: у линейного дешифратора число входов каждого элемента И последнего (и единственного) каскада равно n (n — число адресных входов), у каскадного оно зависит от способа разбиения на группы, однако оно всегда меньше л, но больше двух, у прямоугольного оно равно двум — минимально возможному числу. Поэтому при большом числе выходов (сотни и более) прямоугольный дешифратор — самый экономичный по оборудованию, чем и объясняется его широкое применение в БИС памяти. При уменьшении числа выходов до нескольких десятков первенство по экономичности переходит к каскадным дешифраторам, а при малом числе выходов самым экономичным (а к тому же и самым быстрым) оказывается линейный дешифратор.
Приведенные оценки справедливы лишь для дешифраторов, построенных непосредственно из логических элементов, например при разработке схемы матричной БИС. При проектировании же блоков из готовых микросхем, когда затраты оборудования оцениваются не числом элементов, а числом корпусов, даже большие дешифраторы экономичнее строить по каскадному принципу, набирая их из микросхем небольших дешифраторов на 8 или 16 выходов.
Дешифраторы, выпускаемые в виде отдельных микросхем, имеют буквенное обозначение ИД. В сериях ТТЛ, в которых элементы И-НЕ наиболее технологичны, дешифраторы обычно имеют инверсные выходы, т.е. активный низкий уровень выходного сигнала. В КМДП-сериях, где элементы ИЛИ-НЕ не менее технологичны, чем И-НЕ, дешифраторы чаще имеют прямые выходы. Стремление возможно полнее использовать выводы типовых корпусов определяет размеры декодеров, выпускаемых в виде СИС. Обычно это 3—8, 4—10, сдвоенный 2—4, а также 4—16, но уже в корпусе с 24 выводами.
| Синякина Г.Е. МММММММММММММММммухамедшиной. |
30. Мультиплексор. Таблица функционирования мультиплексора. Мультиплексором называются комбинационные устройство, обеспечивающее передачу в желаемом порядке цифровой информации, поступающей по нескольким входам на один выход. Электронная схема по преобразованию параллельного кода в последовательный.
УГО мультиплексора, имеющего 8 информационных входов, 3 адресных входа, вход разрешения V, и два выхода (прямой инверсный) показано на рисунке (*Вход разрешения V используется для расширения функциональных возможностей мультиплексора, например, позволяет увеличивать число коммутируемых информационных входов):

 разрешение
разрешение
 запрет
запрет
A0, A1, A2 – адресные входы. От их состояния происходит выбор одного разряда D
Разработка формул и таблиц
| A0 | A1 | A2 | Вых |
| | | | Д0 |
| | | | Д1 |
| | | | Д2 |
| | | | Д3 |
| | | | Д4 |
| | | | Д5 |
| | | | Д6 |
| | | | Д7 |
Формула:
Вых=V( 

| Синякина Г.Е. МММММММММММММММммухамедшиной. |
31. Счетчик Счётчики используются для построения схем таймеров или для выборки инструкций из ПЗУ в микропроцессорах. Они могут использоваться как делители частоты в управляемых генераторах частоты (синтезаторах). При использовании в цепи ФАП счётчики могут быть использованы для умножения частоты как в синтезаторах, так и в микропроцессорах.
Простейший вид счётчика — двоичный может быть построен на основе T-триггера. T-триггер изменяет своё состояние на прямо противоположное при поступлении на его вход синхронизации импульсов. Для реализации T-триггера воспользуемся универсальным D-триггером с обратной связью, как это показано на рисунке 1.
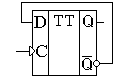
Рисунок 1. Реализация счетного T-триггера на универсальном D-триггере
Так как схема T-триггера при поступлении на вход импульсов меняет свое состояние на противоположное, то её можно рассматривать как счётчик, считающий до двух. Временные диаграммы сигналов на входе и выходах T-триггера приведены на рисунке 2.
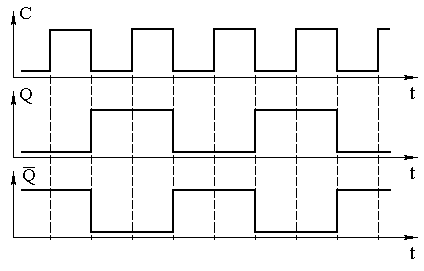
Рисунок 2 Временные диаграммы сигналов на входе и выходах T-триггера
Обычно требуется посчитать большее количество импульсов. В этом случае можно использовать выходной сигнал первого счетного триггера как входной сигнал для следующего триггера, то есть соединить триггеры последовательно. Так можно построить любой счётчик, считающий до максимального числа, кратного степени два. Такой счетчик называется двоичным счетчиком, а тот факт, что состояние триггеров меняется на противоположное в различные моменты времени по мере распространения цифрового сигнала, отображается термином: асинхронный двоичный счетчик.
Схема счётчика, позволяющего посчитать любое количество импульсов, меньшее шестнадцати, приведена на рисунке 3. Количество поступивших на вход импульсов можно узнать, подключившись к выходам счётчика Q0 … Q3. Это число будет представлено в двоичном коде.

Рисунок 3. Схема четырёхразрядного счётчика, построенного на универсальных D-триггерах
Для того чтобы разобраться, как работает схема двоичного счётчика, воспользуемся временными диаграммами сигналов на входе и выходах этой схемы, приведёнными на рисунке 4.

Рисунок 4 Временная диаграмма четырёхразрядного счётчика
Пусть первоначальное состояние всех триггеров счётчика будет нулевым. Это состояние мы видим на временных диаграммах. Запишем его в таблицу 1. После поступления на вход счётчика тактового импульса (который воспринимается по заднему фронту) первый триггер изменяет своё состояние на противоположное, то есть единицу.
Запишем новое состояние выходов счётчика в ту же самую таблицу. Так как по приходу первого импульса изменилось состояние первого триггера, то этот триггер содержит младший разряд двоичного числа (единицы). В таблице поместим его значение на самом правом месте, как это принято при записи любых многоразрядных чисел. Здесь мы впервые сталкиваемся с противоречием правил записи чисел и правил распространения сигналов на принципиальных схемах.
Подадим на вход счётчика ещё один тактовый импульс. Значение первого триггера снова изменится на прямо противоположное. На этот раз на выходе первого триггера, а значит и на входе второго триггера сформируется задний фронт. Это означает, что второй триггер тоже изменит своё состояние на противоположное. Это отчётливо видно на временных диаграммах, приведённых на рисунке 4. Запишем новое состояние выходов счётчика в таблицу 1. В этой строке таблицы образовалось двоичное число 2. Оно совпадает с номером входного импульса.
Продолжая анализировать временную диаграмму, можно определить, что на выходах приведённой схемы счётчика последовательно появляются цифры от 0 до 15. Эти цифры записаны в двоичном виде. При поступлении на счётный вход счётчика очередного импульса, содержимое его триггеров увеличивается на 1. Поэтому такие счётчики получили название суммирующих двоичных счётчиков.
Таблица 1. Изменение уровней на выходе суммирующего счётчика при поступлении на его вход импульсов.
| номер входного импульса | Q3 | Q2 | Q1 | Q0 |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
Условно-графическое обозначение суммирующего двоичного счетчика на принципиальных схемах приведено на рисунке 5. В двоичных счётчиках обычно предусматривают вход обнуления микросхемы R, который позволяет записать во все триггеры счётчика нулевое значение. Это состояние иногда называют исходным состоянием счётчика.

Рисунок 5. Четырёхразрядный двоичный счётчик
Существуют готовые микросхемы асинхронных двоичных счётчиков. Классическим примером такого счётчика является микросхема 555ИЕ5. Подобные схемы существуют и внутри САПР программируемых логических интегральных схем.
Двоичные вычитающие асинхронные счётчики
Счётчики могут не только увеличивать своё значение на единицу при поступлении на счётный вход импульсов, но и уменьшать его. Такие счётчики получили название вычитающих счётчиков. Для реализации вычитающего счётчика достаточно чтобы T-триггер изменял своё состояние по переднему фронту входного сигнала.
Изменить рабочий фронт входного сигнала можно инвертированием этого сигнала. В схеме, приведенной на рисунке 6, для реализации вычитающего счётчика сигнал на входы последующих триггеров подаются с инверсных выходов предыдущих триггеров.

Рисунок 6 Схема четырёхразрядного двоичного вычитающего счётчика, построенного на универсальных D-триггерах
Временная диаграмма этого счётчика приведена на рисунке 7. По этой диаграмме видно, что при поступлении на вход счётчика первого же импульса на выходах появляется максимально возможное для четырёхразрядного счётчика число 1510. При поступлении следующих импульсов содержимое счётчика уменьшается на единицу.

Рисунок 7. Временная диаграмма четырёхразрядного вычитающего счётчика
Это вызвано тем, что при поступлении переднего фронта тактового импульса первый триггер переходит в единичное состояние. В результате на его выходе тоже формируется передний фронт. Он поступает на вход второго триггера, что приводит к записи единицы и в этот триггер. Точно такая же ситуация складывается со всеми триггерами счётчика, то есть все триггеры перейдут в единичное состояние. Для четырёхразрядного счётчика это и будет число 1510. Запишем новое состояние вычитающего счётчика в таблицу 2.
Следующий тактовый импульс приведёт к изменению состояния только первого триггера, так как при этом на его выходе сформируется задний фронт сигнала. Запишем и это состояние в таблицу 2. Обратите внимание, что при поступлении каждого последующего импульса содержимое счётчика, построенного по анализируемой схеме, уменьшается на единицу. Этот процесс продолжается до тех пор, пока состояние счётчика не станет вновь равно 0. При поступлении новых тактовых импульсов процесс повторяется снова.
Все возможные состояния логических сигналов на выходах вычитающего счётчика, при поступлении на счётный вход схемы тактовых импульсов приведены в таблице 2. Таблица 2 фактически повторяет временные диаграммы, приведённые на рисунке 7, однако она более наглядно представляет физику работы счётчика. Просто мы при работе с числами привыкли иметь дело с цифрами, а не с напряжениями, тем более в зависимости от времени.
Таблица 2. Изменение уровней на выходе вычитающего счётчика при поступлении на его вход импульсов.
| номер входного импульса | Q3 | Q2 | Q1 | Q0 |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
Для тех, кто привык работать с реально выпускаемыми микросхемами средней интеграции, следует обратить внимание, что для примера были использованы D-триггеры, работающие по заднему фронту. Микросхемы, выпускаемые промышленностью, например, 1533ТМ2 (два D-триггера в одном корпусе) или SN74LVC1G79 (микросхемы малой логики) срабатывают по переднему фронту, поэтому схемы для суммирующего и вычитающего счётчика поменяются местами.
Следует отметить, что при применении для реализации двоичных счетчиков современных схем большой интеграции, таких как программируемые пользователем вентильные матрицы FPGA, мы можем применять D-триггеры срабатывающие как по переднему (нарастающему), так и по заднему (спадающему фронту).
| Синякина Г.Е. МММММММММММММММммухамедшиной. |
Литература: - Микушин А.В., Сажнев А.М., Сединин В.И. Цифровые устройства и микропроцессоры. СПб, БХВ-Петербург, 2010.
- Угрюмов Е. П. Цифровая схемотехника. СПб, БХВ-Петербург, 2004.
- Шило В. Л. Популярные цифровые микросхемы. М, Радио и связь, 1987.
- Дж. Ф. Уэкерли Проектирование цифровых устройств. М, Постмаркет, 2002.
5.http://digteh.ru/digital/




 разрешение
разрешение запрет
запрет








