Краткие методические указания к решению задачи 2

Последовательность действия при выполнении пункта 1 задачи следующая:

Во-первых, производится ранжирование данных информационной таблицы по возрастанию признака 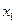. Для этого составляется промежуточная табл.3.

Таблица 3

Номер п/п	Признак	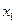Результативные признаки
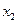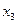	3240,00	1650,00
	4200,00	2350,00
	4400,00	2500,00
…
	…	…	…
Итого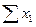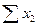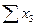

В таблице значения признака 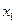располагаются по возрастанию от наименьшего к наибольшему. Соответственно вносятся в таблицу значения всех других результативных признаков. Например, если наименьшее значение признака 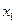составляет 3240, а ему соответствуют значения результативных признаков 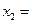1650 и 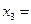5, то эти значения вносятся в первую строку промежуточной таблицы 3. Последующее по возрастанию значение признака 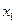- 4200, соответствующие ему значения результативных признаков 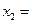2350 и 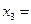6 вносятся во вторую строку таблицы и т.д.

Во-вторых, определяется число групп и величина интервала. Число групп определяется по формуле Стерджесса:

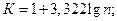
где 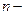число единиц наблюдения.

Формула Стерджесса пригодна при условии приближения распределения наблюдаемых единиц совокупности к нормальному распределению. При этом применяются равные интервалы. Величина интервала определяется по формуле

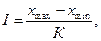
где 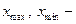наибольшее и наименьшее значение признака 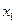, округление 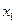производится до целого большего числа.

В –третьих, образуются группы с равными интервалами по признаку 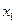. Для этого к минимальному значению признака 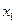( 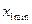), которое является нижней границей признака для первой группы, прибавляется найденной значение интервала 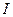,т.е. верхняя граница для первой группы определяется как 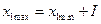. Это же значение является нижней границей для второй группы, пример распределения верхних и нижних границ признака приведен в табл.4.

Таблица 4.

Номер группы	Нижняя граница признака	Верхняя граница признака
	…	…
	…	…
	…	…

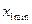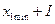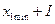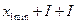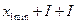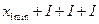В-четвертых, все единицы наблюдения и, соответственно, значения результативных признаков распределяются в вышеуказанные группы.

В-пятых, производится расчет показателей по группам согласно пунктам а, б, в. Итоговые групповые абсолютные величины определяются простым суммированием числа единиц наблюдения и индивидуальных значений признаков по каждой группе в отдельности.

Относительные величины, выраженные в процентах, исчисляются по общим арифметическим правилам в виде пропорции.

Средние величины по группам и их дисперсии определяются по уже приведенным формулам (2) и (5) задачи 1. Расчеты производятся по каждому признаку - и по каждой группе в отдельности.

В-шестых, составляются выходные статистические таблицы.

Ниже для иллюстрации приводятся результаты расчетов по пункту 1 (подпункты а, б, в), выполненные по данным базовой информационной таблицы.

1. Число групп и величина интервала:

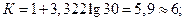
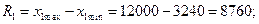
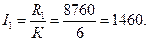
2. Выходные статистические таблицы (табл.7-10)

Таблица 7