Составление алгоритма решения. Элементарность математической модели позволяет выполнить стандартный вариант алгоритма решения в один шаг (рис
Элементарность математической модели позволяет выполнить стандартный вариант алгоритма решения в один шаг (рис. 4.5). Для дальнейшего программирования полученная стандартная схема дополнена двумя условно-линейными вариантами алгоритма (рис. 4.6).
Программирование задачи
Программирование задачи требует предварительного овладения правилами записи составных логических выражений на конкретном языке программирования.
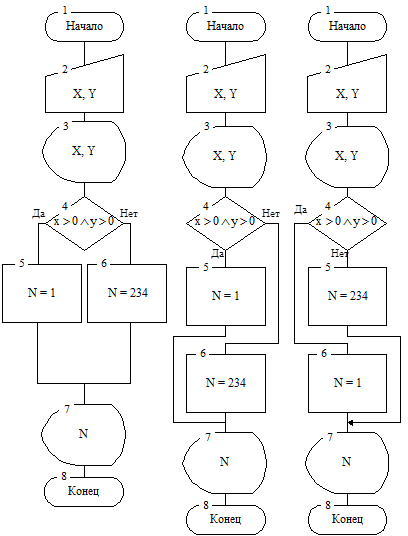
Вариант 1 Вариант 2
Рис. 4.5. Схема Рис. 4.6. Условно-линейные
алгоритма варианты схемы
В Си/Си++, как и в математике, существует возможность записи сложных логических выражений, при этом каждому из логических символов соответствует определённое обозначение по типу операций отношения (табл. 4.5).
Таблица 4.5
| Обозначение в математике | Обозначение в Си/Си++ | |||
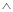 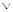 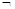 | && | | ! | |||
Общая структура логического выражения имеет вид:
А 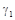 В [
В [ 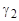 C
C 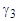 . . .
. . . 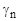 Z]
Z]
, где А В . . . Z – логические операнды (ИСТИНА, ЛОЖЬ);
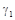
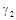 . . .
. . . 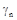 – логические операции (И, ИЛИ).
– логические операции (И, ИЛИ).
[ ] – признак необязательности содержимого.
Структура простейшего логического выражения аналогична приведенной для операций отношения
А 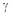 В
В
, где А и В – логические операнды (ИСТИНА, ЛОЖЬ);
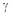 – логическая операция (И, ИЛИ).
– логическая операция (И, ИЛИ).
Правила составления и выполнения логических выражений
В качестве операндов А, В, С, …, Z могут использоваться константы, переменные, выражения любых типов. Результат вычисления каждого операнда оценивается как ИСТИНА (единица, не ноль) или ЛОЖЬ (ноль).
Выполнение простейшего логического выражения осуществляется слева направо. Если значение первого операнда позволяет определить результат операции, второй операнд не вычисляется.
Результат выполнения логической операции – целая константа 1 (ИСТИНА) или 0 (ЛОЖЬ). Так, для операции && (И) результат есть 1, если оба операнда ненулевые. Если один из операндов – ноль, результат тоже 0. Например, в операции х && у (х=1.2, у=0.7) результат есть 1, т.к. оба операнда не нулевые. Если же х=0, то независимо от значения у результатом вычисления будет 0. Для операции | | (ИЛИ) результат есть 1, если любой (оба) из операндов имеет ненулевые значения. В противном случае (оба операнда – нулевые) результат – 0.
Составные логические выражения могут использоваться в качестве выражения P в условных операторах if.
При выполнении составных логических выражений в Си/Си++ существует следующая иерархия:
· отрицание;
· арифметические операции;
· операции отношения;
· операция «И»;
· операция «ИЛИ».
В сложных составных выражениях одноранговые операции И (ИЛИ) выполняются слева направо. При этом результат проверки первой (предыдущей) становится логическим операндом для второй (последующей). Например, в выражении a<b || d>k || z!=5 сначала определяются результаты проверки операций отношения (a<b, d>k, z!=5), а затем логическое выражение (две операции ИЛИ) пооперационно слева направо.
При необходимости нарушить порядок выполнения операций отношения используют, как и в арифметическом выражении, круглые скобки.
Соответствие записей некоторых простых и составных логических выражений в математике и на языке программирования Си/Си++ демонстрируются типовыми примерами в табл. 4.6.
Таблица 4.6
| Обозначение в математике | Обозначение в Си/Си++ |
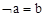 | ! a = = b |
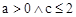 | a>0 && c<=2 |
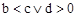 | b<c | | d>0 |
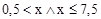 | 0.5<x && x£7.5 |
Окончание табл. 4.6
| Обозначение в математике | Обозначение в Си/Си++ |
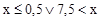 | x<=0.5 | | 7.5<x |
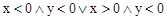 | x<0 && y<0 | | x>0 && y<0 |
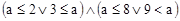 | (a<=2 | | 3<=a) && (a<=8 | | 9<=a) |
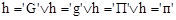 | h= =‘G’ || h= =‘g’ || h= =‘П’ || h= =‘п’ |
С учетом изложенного, осуществим программирование задачи о положении точки. Идентификация переменных представлена в табл. 4.7.
Таблица 4.7
| Обозначения в алгоритме | X | Y | N |
| Обозначения в программе | x | y | n |
На основании условно-линейных схем алгоритма, правил записи логических выражений и таблицы идентификации, составим программы решения с использованием укороченного и полного условных операторов.
Составление программы по условно-линейной схеме варианта 1
Условно-линейная схема алгоритма с последовательным расположением ветвей «ДА», «НЕТ», может быть реализована в программу только с использованием полного if.
Вариант программы имеет вид:
/* Задача 4.2. Составное условие. Полный if */
/* Разработал студент гр. А031 Степанов И.Г. */
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
main( )
{
float x, y;
int n;
scanf(“%5f%5f”, &x, &y);
printf(“\n X=%7.3f Y=%8.3f\n”, x, y);
if( x>0. && y>0. ) /* начало полного оператора if */
n=1; /* ветвь “ДА” */
else
n=234; /* ветвь “НЕТ” */
printf(“\n N=%3d\n”, n);
}
0.0703.000 – данные для проверки ветви 1
12.30-104. – данные для проверки ветви 234
-17.5-8.94 – данные для расчёта
Первые две строки численных значений позволяют проверить работоспособность каждой ветви программы. Третья – задаёт текущие значения, требующие реальной проверки.
Результаты счета представлены в приложении 4.3 (а, б, в).
Составление программы по условно-линейной схеме варианта 2
Условно-линейная схема алгоритма с последовательным расположением ветвей «НЕТ», «ДА», может быть реализована в программу только с использованием структуры из укороченного if и двух goto.
Вариант программы имеет вид:
/* Задача 4.2. Составное условие. Укороченный if */
/* Разработал студент гр. А031 Степанов И.Г. */
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
main( )
{
float x, y;
int n;
scanf(“%5f%5f”, &x, &y);
printf(“\n X=%7.3f Y=%8.3f\n”, x, y);
if( x>0. && y>0. ) goto M1; /* укороченный оператор if */
n=234; /* ветвь “НЕТ” */
goto M2;
M1: n=1; /* ветвь “ДА” */
M2: printf(“\n N=%3d\n”, n);
}
0.0703.000 – данные для проверки ветви 1
12.30-104. – данные для проверки ветви 234
-17.5-8.94 – данные для расчёта
Первые две строки численных значений позволяют проверить работоспособность каждой ветви программы. Третья – задаёт текущие значения, требующие реальной проверки.
Результаты счета представлены в приложении 4.4 (а, б, в).
Составление программ завершает этап создания программного продукта задачи с одним составным условием.
Предлагаемая технология универсальна и применима для предмашинной подготовки задач с проверкой одного любого составного условия.
