ДМ функции алгебра логики, реализация функций формулами, канонические формы

E²={0,1}; f(x₁,…,x_n)-ф-ия алгебра логики, если переменные x₁,…, x_n определены на E² и зн‑ия ф-ии f на любом наборе переменных принадлежат E²

Способы задания ф-ий: табличный, в виде формул.
Число булевых ф-ий от n переменных = 2ⁿ

Ф-ия f(x₁…x_i…x_n) существенно зависит от x_i, если $a₁…a_n такой, что f(a₁…a_i_‑10a_i₊₁…a_n)≠f(a₁…a_i_-11a_i₊₁…a_n). Иначе переменная называется фиктивной.S

Функции называются равными, если одну можно получить из другой путем удаления и добавления фиктивных переменных (или они принимают на всех возможных наборах одинаковые значения)

Элементарные ф-ии:

x&y

xÚy

x®y

x~y

xÅy

x|y

x¯y

отр

кон

диз

импл

экв

слож

штрих шеффера

стрелка пирса

f(A₁…A_n) – формула, если A₁…A_n – формулы либо переменные

Каждая формула реализует некоторую ф-ию (можно сделать табличку). Ф-лы эквивалентны, если реализуемые ими ф-ии равны.

Любую булеву ф-ию м. представить в виде f(x₁...x_n)ё= 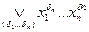ДМ функции алгебра логики, реализация функций формулами, канонические формы - student2.ru -СДНФ

Как построить СДНФ: СДНФ содержит столько слагаемых, сколько 1 в таблице. Каждое слагаемое содержит все перменные. Переменные входят с отрицаниями или без в зависимости от значения переменной. Пример:

x
y
z
f(x,y,z)

ДМ функции алгебра логики, реализация функций формулами, канонические формы - student2.ru

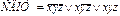ДНФ –дизъюнкция элементарных конъюнкций, т.е.D=k₁Úk₂Ú…Úk_m, где элем. кон. 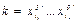ДМ функции алгебра логики, реализация функций формулами, канонические формы - student2.ru (в элем. кон. все перемен. различны. r - ранг конъюнкции). Минимальная ДНФ – ДНФ, содержащая наименьшее число вхождений переменных. Кратчайшая ДНФ – ДНФ, содержащая наим. число элем. кон.

2. ДМ полнота и замкнутость систем функций. теорема о функциональной полноте

f(A₁…A_n) – формула, если A₁…A_n – формулы либо переменные

Пусть P={f₁f₂…} – система ф-ий изP₂. Система ф-ий P функционально полна в P₂, если "fÎP₂ м.б. представлена в виде формулы над P. Примеры полных в P₂ систем ф-ий: P₂, {&,Ú,Ø},

{&,Ø}, {Ú,Ø}, {0,1, x&y, xÅy}, {|}, {Ú,®}

Пусть MÉP₂. Замыканием мн-ва M наз-ся мн-во всех булевых ф‑ий, представимых в виде ф-лы над M. Обозн [M].

Пр.: M=P₂ Þ [M]=P₂; M={1, x₁Åx₂} Þ [M]={f: f=c₀Åc₁x₁Å…Åc_nx_n}

Класс M – замкнутый, если M=[M]. Пр.: P₂-замкнутый класс

Классы ф-ий: T₀={f: f(0…0)=0} – класс ф-ий, сохраняющих константу 0; T₁ – класс ф-ий, сохр-х константу 1; S -класс самодвойственных ф-ий (на противоположенных наборах принимают противоположные значения); M-класс монотонных ф-ий ("a,b:a<b f(a)£f(b)); L-класс линейных ф-ий

			x	x	x&y	xÚy	x®y	x~y	xÅy	x\|y	x¯y
T0	+	-	+	-	+	+	-	-	+	-	-
T1	-	+	-	-	+	+	+	+	-	-	-
S	-	-	+	+	-	-	-	-	-	-	-
M	+	+	+	-	+	+	-	-	-	-	-
L	+	+	+	+	-	-	-	+	+	-	-
				отр	кон	диз	импл	экв	слож	штрих шеффера	стрелка пирса

[Т] о функциональной полноте: пусть P={f₁f₂…}-произв. сист. ф‑ий из P₂. Для того, чтобы сист. ф-ий была функционально полной в P₂ н. и д., чтобы она целиком не принадлежала ни одному из замкнутых классов T₀, T₁, S, L, M.

Пр.: {xÚy, Øx}