Синтез схем со многими выходами
Закон функционирования комбинационной схемы, имеющей n входов и m выходов, записывается системой из m булевых функций от n переменных. Такую схему можно представить в виде набора m не связанных между собою подсхем, каждая из которых реализует только одну функцию системы. Каждую подсхему можно реализовать по минимальной ДНФ соответствующей функции. Однако такой подход к построению комбинационных схем не рационален с точки зрения затрат оборудования.
Минимизация систем со многими выходами заключается в нахождении таких выражений для совокупности булевых функций, в которых наиболее полно используются члены, общие для нескольких функций.
Один из методов упрощения схем заключается в том, что одни булевы функции выражаются через другие.
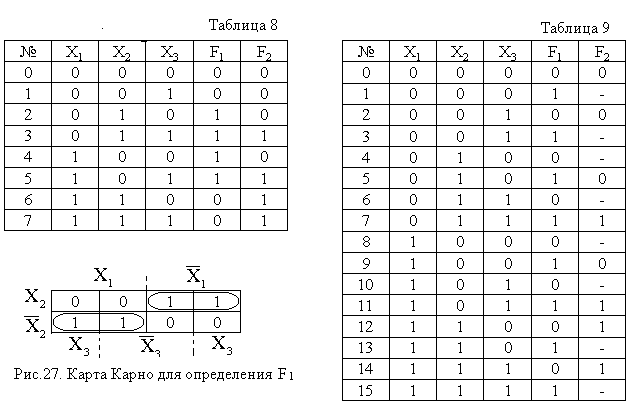
Пример. Функции F1 и F2 заданы таблицей 8. Будем считать функцию F1 функцией трех аргументов, а функцию F2 - функцией четырех аргументов: X1, X2, X3, F1. Минимальную ДНФ для функции F1 находим с помощью карты Карно (рис. 27):
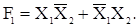
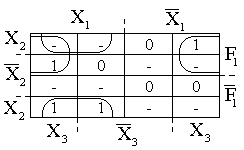 Рис. 28. Карта Карно для определения F2 Рис. 28. Карта Карно для определения F2 | Для определения функции F2 строим таблицу истинности следующим образом (см. табл.9). Рассматриваем набор с номером 0. При X1=X2 =X3=0 F1 и F2 равны нулю. В последней колонке таблицы ставим в строке X1=X2= =X3=F1=0 F2=0. На наборе №1 (Табл.9) F1=1, что не соответствует заданному условию ( табл.8 ), поэтому ставим в последней колон- ке прочерк (запрещенный набор). Значения функции F2 на остальных наборах определяются аналогично. Далее определяем минимальную ДНФ для функции F2 с помощью карты Карно (рис. 28). |

Нужно проверить два варианта: F1(X1, X2, X3, F2) и F2(X1, X2, X3, F1) и выбрать тот из них, который лучше с точки зрения минимума сложности всего устройства. В данном примере второй вариант не дает выигрыша.
Литература
1. Сигорский В. П. Математический аппарат инженера. - К.: Техника, 1975.- 766 с.; ил.
2. Вавилов Е. П., Портной Г. П. Синтез схем электронных цифровых машин. - М.: Советское радио, 1963.-437с. ил.
3. Вавилов Е. П., Егоров Б. М. Синтез схем на пороговых элементах. - М.: Советское радио, 1970.-367с.
КОНЕЧНЫЕ АВТОМАТЫ
Основные понятия и определения
Различают два типа дискретных устройств автоматики. В устройствах первого типа выходные сигналы в каждый момент времени однозначно определяются входными сигналами в этот же момент времени и не зависят от того, какие значения принимали входные сигналы в предшествующие моменты времени. В устройствах этого типа отсутствуют элементы памяти. Такие устройства получили название комбинационные.
Устройства второго типа характеризуются наличием элементов памяти. В этих устройствах сигналы на выходе зависят не только от входных сигналов в данный момент времени, но и от того, какие значения входные сигналы принимали в предшествующие моменты времени. Устройства второго типа получили название автоматов. ”Память” автомата определяется различными внутренними состояниями, которые он может принимать под воздействием входных сигналов и сохранять их при изменении последних.
Автоматом называют дискретный преобразователь информации, способный принимать различные состояния, переходить под воздействием входных сигналов из одного состояния в другое и выдавать выходные сигналы.
Если множество состояний автомата, а также множества входных и выходных сигналов конечны, то автомат называют конечным автоматом. Все реальные автоматы конечны.
Информацию, поступающую на вход автомата, и преобразованную (выходную) информацию принято кодировать конечной совокупностью символов. Эту совокупность называют алфавитом, отдельные символы, образующие алфавит, - буквами, а любые конечные упорядоченные последовательности букв данного алфавита - словами в этом алфавите. Например, в алфавите X={x1,x2}, словами будут: (x1), (x2), (x1x1), (x2x1x2) и т.д.
Процесс дискретного преобразования информации автоматом можно описать с помощью алфавитных операторов.
Алфавитным оператором Fназывают любое соответствие (функцию) между словами входного и выходного алфавитов.
Автоматы функционируют в дискретные моменты времени, которые обычно обозначают натуральными числами t=0,1,2,...,n. В каждый момент дискретного времени на вход автомата поступает один сигнал (буква), фиксируется определенное состояние автомата и с выхода снимается один сигнал.
Реальные автоматы могут иметь несколько входов и несколько выходов. В некоторых случаях удобно заменить такие автоматы автоматами с одним входом и одним выходом. Для этого достаточно закодировать соответствующим образом входные и выходные сигналы исходного автомата. Если, например, автомат имеет два входа, на каждый из которых подаются сигналы 0 или 1, то все возможные комбинации входных сигналов можно закодировать четырьмя буквами: (0,0)=X1, (0,1)=X2, (1,0)=X3, (1,1)=X4. При этом автомат, имеющий два входа, можно рассматривать как автомат с одним входом, на который подаются сигналы в четырехбуквенном алфавите.
Для того, чтобы задать конечный автомат, нужно указать:
- множество возможных входных сигналов X={x1,x2,...,xm};
- множество возможных выходных сигналов Y={y1,y2,...,yk};
- множество возможных внутренних состояний автоматаA={a1,a2,...,an};
- функцию переходов, определяющую состояние автомата a(t+1) в момент дискретного времени t+1 в зависимости от состояния автомата a(t) и значения входного сигнала X(t) в момент времени t;
-функцию выходов, определяющую зависимость выходного сигнала автомата y(t) от состояния автомата и значения входного сигнала в момент времени t. Кроме того на множестве состояний автомата фиксируют одно из внутренних состояний в качестве начального состояния.
Существует два типа конечных автоматов. Для автоматов первого типа функции переходов и выходов имеют вид:
a(t+1)=f[a(t),x(t)], y(t)=j[a(t),x(t)].
У автоматов этого типа выходной сигнал в данном такте определяется внутренним состоянием и входным сигналом в данном такте. Такие автоматы получили название автоматы Мили.
Автоматы второго типа отличаются тем, что выходной сигнал такого автомата в данном такте определяется только внутренним состоянием автомата в этом же такте. Функции переходов и выходов для автомата второго типа, заданные на множестве входных сигналов X={x1,x2,...,xm}, множестве внутренних состояний B={b1,...,bn} и множестве выходных сигналов Y={y1,...,yk} имеют вид:
b(t+1)=f[b(t),x(t)], y(t)= j[b(t)].
Такие автоматы называются автоматами Мура.
Функции переходов и выходов можно задать таблицами переходов и выходов, либо графом автомата. На рис.29 приведены таблицы переходов и выходов автомата Мили.
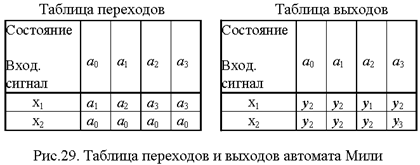
В клетку таблицы переходов, находящуюся на пересечении столбца с буквой aiи строки с буквой xj, записывается состояние автомата f(ai,xj), в которое он переходит из состояния aiпри подаче на вход сигнала xj. Аналогично записывается в таблице выходов сигнал y, который формируется автоматом при таком переходе.
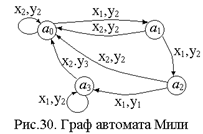
При построении графа автомата вершины графа отождествляются с внутренними состояниями автомата. Каждая ветвь отмечается входным сигналом, вызывающим в автомате соответствующий данной ветви переход, и выходным сигналом, который возникает при этом переходе. На рис.30 приведен граф автомата, соответствующий автомату Мили, заданному таблицами на рис.29.
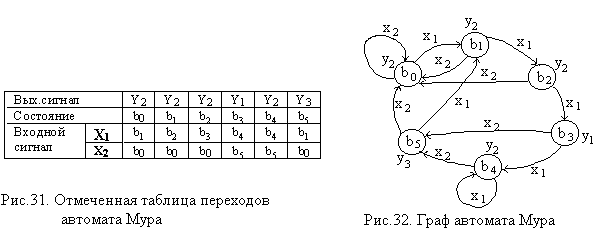
Для автомата Мура функции переходов и выходов можно задать одной таблицей, которая называется отмеченной таблицей переходов. Отмеченная таблица переходов автомата Мура строится также, как и таблица переходов автомата Мили, но над символами каждого внутреннего состояния записываются выходные сигналы, которые автомат выдает в данном состоянии. На графе автомата Мура значения выходных сигналов записываются около узлов. На рис.31 и32 приведены в качестве примера отмеченная таблица переходов и граф автомата Мура.
Работу автомата при произвольной последовательности входных сигналов можно проследить с помощью ленты автомата. Лента автомата представляет собой
 | таблицу, в которой указываются такты работы автомата, значения входного сигнала в каждом такте и значения внутреннего состояния и выходного сигнала в каждом такте. Пример ленты автомата, заданного таблицами переходов и выходов, приведенными на рис. 29, показан на рис. 33. |
| Такт | ||||||||||||
| Вход. сигнал | x1 | x2 | x1 | x1 | x1 | x2 | x2 | x2 | x1 | x2 | x2 | x2 |
| Состояние | a0 | a1 | a0 | a1 | a2 | a3 | a0 | a0 | a0 | a0 | a0 | a0 |
| Выход. сигн. | y2 | y2 | y2 | y2 | y1 | y3 | y2 | y2 | y2 | y2 | y2 | y2 |
Рис. 33. Лента автомата
Два автомата, у которых совпадают как входные, так и выходные алфавиты, называются эквивалентными, если для любого входного слова выходное слово одного автомата совпадает с выходным словом другого автомата. При этом перед подачей входного слова оба автомата должны находиться в начальных состояниях.
Для любого автомата Мили существует эквивалентный ему автомат Мура и наоборот.
