Автоматическое доказательство теорем. Метод резолюций

Пусть имеется множество формул Г = {A₁, A₂, …, A_n} и формула B. Автоматическим доказательством теоремы B называют алгоритм, который проверяет вывод A₁, A₂, …, A_n ⊢B. Выражение читается следующим образом: "Если посылки A₁, A₂, …, A_n истинны, то истинно заключение B".

Проблема доказательства в логике состоит в том, чтобы установить, что если истинны формулы A₁, A₂, …, A_n, то истинна формула B. Доказательство этого равносильно доказательству общезначимости некоторой формулы. Наиболее эффективно доказательство общезначимости формул осуществляется методом резолюций. Процедура поиска доказательства методом резолюций фактически является процедурой поиска опровержения, т. е. вместо доказательства общезначимости формулы доказывается, что отрицание формулы противоречиво.

При изложении метода резолюций обычно употребляется следующая терминология.

Литерой называется выражение A или ØA. Литеры A и ØA называются контрарными, а множество {A, ØA} – контрарной парой.

Дизъюнкт – это дизъюнкция литер (или элементарная дизъюнкция). Дизъюнкт называется пустым, (обозначается ), если он не содержит литер. Пустой дизъюнкт всегда ложен, так как в нем нет литер, которые могли бы быть истинными при любых наборах переменных.

Рассмотрим применение метода резолюций к исчислению высказываний.

Правилом резолюции называют следующее правило вывода:

.

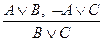Правило резолюции можно записать в следующем виде: AÚB, ØAÚC ⊢BÚC.

Дизъюнкт BÚC называется резольвентой дизъюнктов AÚB и ØAÚC по литере A: BÚC = res_A(AÚB и ØAÚC).

Если дизъюнкты не содержат контрарных литер, то резольвенты у них не существует. Для дизъюнктов A и ØA резольвента есть пустой дизъюнкт: res_A(A, ØA) = .

Пример 3.4.

Пусть F = AÚBÚC, G = ØAÚØBÚD.

Тогда

res_A(F, G) = BÚCÚ ØBÚD.

res_B(F, G) = AÚCÚØAÚD.

res_C(F, G) не существует.

Метод резолюций соответствует методу доказательства от противного. Условие A₁, A₂, …, A_n ⊢ B равносильно условию A₁, A₂,…, A_n, ØB ⊢ .

Алгоритм построения вывода методом резолюций.

Шаг 1. Все формулы посылок A₁, A₂, …, A_n и формулу отрицания заключения ØB привести к КНФ.

Шаг 2. Выписать множество K дизъюнктов всех посылок A₁, A₂, …, A_n и отрицания заключения ØB: K={D₁, D₂, …, D_n}.

Шаг 3. Выполнить анализ пар множества K правилу: если существуют дизъюнкты D_i, D_j , один из которых D_i, содержит переменную A_i, а другой D_j –отрицание ØA_i , то соединить эту пару логической связкой дизъюнкции D_iÚD_j и сформировать по правилу резолюции новый дизъюнкт – резольвенту, исключив содержащих контрарные литеры A_i и ØA_i.

Шаг 4. Процесс продолжаем. Если он заканчивается пустым дизъюнктом, то вывод обоснован.

Изложенный алгоритм назывется резолютивным выводом из K.

Возможны три случая.

1. Среди множества дизъюнктов нет содержащих контрарные литеры. Это означает, что формула B не выводима из множества формул A₁, A₂, …, A_n.

2. После очередного применения правила резолюции получен пустой дизъюнкт. Это означает, что формула B выводима из множества формул A₁, A₂,…, A_n .

3. Процесс зацикливается, т. е. получаются все новые резольвенты, среди которых нет пустых.

Пример 3.5.

Применить для примера 3.2 A ® (B ® C), AÙB ⊢ C метод резолюций. Для этого нужно проверить вывод A ® (B ® C), AÙB, ØC ⊢ .

Алгоритм решения.

Шаг 1. Привести к КНФ формулы A® (B® C), AÙB, ØC.

A®(B® C) º ØAÚ(B® C) º ØAÚØBÚC.

Формулы AÙB, ØC уже находятся в КНФ.

Шаг 2. Составим множество К дизъюнктов:

К = {ØA Ú ØB Ú C, A, B, ØC}.

Шаг 3. Построим резолютивный вывод из K. Выпишем по порядку все дизъюнкты из K:

1) ØA Ú ØB Ú C;

2) A;

3) B;

4) ØC;

Вместо пары дизъюнктов, содержащих контрарные литеры запишем их резольвенту (в скобках указаны номера формул, образующих резольвенту):

5) ØBÚC. (1, 2)

6) C. (3, 5)

7) . (4, 6)

Вывод заканчивается пустым дизъюнктом, что является обоснованием вывода A ® (B ® C), AÙB ⊢ C.

Задания

1. Установить правильность рассуждения, построив вывод исчисления высказываний.

2. Проверить вывод методом резолюций.

Варианты индивидуальных заданий

Вариант № 1

1. На работу в эту организацию принимают, если пройдешь собеседование и будешь аттестован положительно. Его не приняли. Значит, он либо не прошел собеседование, либо не был положительно аттестован.

2. X, B, ( CÙX)®Ø B ⊢ C.

Вариант № 2

1. Если светофор красный, то проезд не разрешен. Проезд разрешен. Значит, светофор не красный.

2. ØA ® (B Ú C), ØA Ú C, ØB⊢ C.

Вариант № 3

1. Если треугольник равносторонний, то его углы равны. Треугольник равносторонний. Следовательно, его углы равны.

2. ((XÙC ) ® ØB ) ⊢ ØC.

Вариант № 4

1. Если ограбление совершил Сидоров, то он знает, где находятся похищенные деньги. Сидоров не знает, где находятся похищенные деньги. Следовательно, он не совершал ограбления.

2. AÚF, A® C, F®D⊢ CÚD.

Вариант № 5

1. Если растение лекарственное, его следует охранять. Это растение не подлежит охране. Следовательно, оно не лекарственное.

2. A, C, (AÙC )® D, D ® F ⊢ F.

Вариант № 6

1. Петров инженер или студент. Он не инженер. Следовательно, он студент.

2. ØA ® (B Ú C), A ® B, ØC⊢ B.

Вариант № 7

1. Если студент занимается не систематически, то он не имеет прочных знаний. Если он не имеет прочных знаний, то он не будет хорошим специалистом. Следовательно, если студент занимается не систематически, то он не будет хорошим специалистом.

2. A, A ® (ØB ®C), B ® D, ØC ⊢ D.

Вариант № 8

1. Это вещество может быть кислотой либо солью. Это вещество не соль. Следовательно, это кислота.

2. (A ® C ) ® (ØA ® B)⊢ A Ú B.

Вариант № 9

1. Если прямая касается окружности, то радиус, проведенный в точку касания, перпендикулярен к ней. Радиус окружности не перпендикулярен к этой прямой. Следовательно, прямая не касается окружности.

2. F Ú C, C ® A, F ® D, D ® A ⊢ A.

Вариант № 10

1. Если человек знает геометрию, то он знает теорему Пифагора. Этот человек не знает теорему Пифагора. Следовательно, он не знает геометрию.

2. ØB ® (D ® C), D, C ® ( A Ú B)⊢ A Ú B.

Вариант № 11

1. Если слово ставится в начале предложения, то оно пишется с большой буквы. Это слово написано с маленькой буквы. Следовательно, это слово не стоит в начале предложения.

2. B ® (C ® A), ØB ® D, D ® C, ⊢ C.

Вариант № 12

1. Если функция четная, то ее график симметричен относительно оси OY. График несимметричен относительно оси OY. Следовательно, функция не является четной.

2. B ® (C ® A), ØB ® E, C, ØE⊢ A

Вариант № 13

1. Если светофор зеленый, то проезд разрешен. Проезд не разрешен. Значит, светофор не зеленый.

2. ØC, D ® C, A ® (ØB ® D), B ⊢ A ® C.

Вариант № 14

1. Если Андрей отсутствовал на работе, он не выполнил задания. Андрей был на работе. Следовательно, он выполнил задание.

2. C ® (B ® A), ØB ® E, C ⊢A Ú E.

Вариант № 15

1. Плох тот солдат, который не мечтает стать генералом. Этот солдат хорош. Следовательно, он мечтает стать генералом.

2. A ® (C ® B), D ® A, C ⊢ D ® B.

Вариант № 16

1. Если треугольник равносторонний, то он равнобедренный. Если треугольник равнобедренный, то углы при основании равны. Следовательно, если треугольник равносторонний, то углы при основании равны.

2. A, X ®C⊢ (A ® ØC) ® ØX.

Вариант № 17

1. Если диагноз подтвердится, то ему придется лечь в больницу. Если он ляжет в больницу, то поездку придется отменить. Диагноз подтвердился. Значит, поездку придется отменить.

2. A ® (C ® B), D ® A, C ⊢D ®B.

Вариант № 18

1. Петров студент или школьник. Он не школьник. Следовательно, он студент.

2. A, A ® (B ®C), ØB ®D, ØC ⊢ D.

Вариант № 19

1. Если я устал, то не могу готовиться к занятиям. Если я не смогу приготовиться к занятиям, я не напишу контрольную работу. Я устал. Значит, я не напишу контрольную работу.

2. B ® (E ®C), E, C ® ( A Ú ØB) ⊢ B ®A.

Вариант № 20

1. Если Сергей победит на соревнованиях, он войдет в сборную страны. Если он войдет в сборную страны, то будет участвовать в чемпионате мира. Следовательно, если Сергей победит на соревнованиях, он будет участвовать в чемпионате мира.

2. G ® (B Ú C), GÚ C, ØB ⊢ C.

Тема 4. НЕЧЕТКАЯ ЛОГИКА

Нечеткая логика отличается от двузначной классической логики тем, что если значения истинности высказывания классической логики могут быть только 0 («ложь») и 1 («истина»), то нечеткая логика допускает несчетное число промежуточных истинностных значений для высказываний в интервале [0, 1].

При описании сложных систем, в которых наряду с количественными данными присутствуют неоднозначные качественные данные, приходится использовать нечеткие понятия и рассуждения. Для формализации таких задач Л. Заде разработал основы математического аппарата, опирающегося на понятия нечетких множеств и нечеткой логики.

Основные понятия нечетких множеств

Пусть М – некоторое множество, рассмотрим какое-либо подмножество А этого множества. Для любого хÎМ имеем хÎА или хÏА. Можно ввести характеристическую функцию подмножества А:

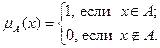
Тогда, например, если M={a, b, c, d, e, f, g, h}и A={a, b, c, d}, имеем:

x	а	b	с	d	е	f	g	h
mA(x)

Для универсального множества М: "х m_M (x) = 1.

Множества, для которых характеристическая функция принимает только значения 0 или 1, будем называть четкими. Классическая логика оперирует с четкими множествами.

Для нечетких множеств характеристическая функция может принимать любые значения из интервала [0,1]. Например,

x	а	b	с	d	е	f	g	h
mA(x)	1,0	0,1	0,8	0,7	0,5	0,2	0,0	0,1
mB(х)	0,1	0,3	0,8	0,9	0,5	0,1	0,0	0,0

Для записи нечетких множеств используется обозначение: А={(х, m_A (х))| "xÎM}. Запись 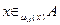характеризует степень принадлежности элемента x множеству A.

Для нечетких множеств определены отношение включения (Ì) и равенства (=):

АÌВ тогда и только тогда, когда "xÎM: m_A (х) £ m_B (х);

А=В тогда и только тогда, когда "xÎM: m_A (х) = m_B (х).

Над нечеткими множествами выполняются операции:

Дополнение А: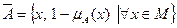

Пересечение: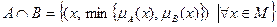

Объединение: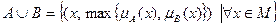

АÈВ={(х, max {m_A (х), m_B (х)})| "xÎM }.

Элементы нечеткой логики

Нечетким высказыванием называется высказывание P, степень истинности которого m_P можно оценить числом из интервала [0, 1], m_P Î [0, 1].

Нечеткой высказывательной переменной X называется нечеткое высказывание X, степень истинности которого может меняться в интервале [0, 1].

Так как степень истинности нечеткого высказывания не связана с сутью высказывания, будем в дальнейшем отождествлять нечеткое высказывание с его степенью истинности аналогично тому, как обычное четкое высказывание отождествлялось с его истинностью или ложностью. Нечеткие высказывания и степень их истинности будем обозначать буквами: P, Q, X, и т. д.

На множестве нечетких высказываний вводятся логические операции, аналогичные операциям алгебры высказываний.

1. Отрицание нечеткого высказывания:ØP= 1 – P.

2. Конъюнкция нечетких высказываний: PÙQ = min(P, Q).

3. Дизъюнкция нечетких высказываний: PÚQ= max(P, Q).

4. Импликация нечетких высказываний: P®Q = max (1 –P, Q).

5. Эквивалентность нечетких высказываний:

P« Q = min (max (1 –P, Q), max (P, 1 –Q)).

Пример 4.1.

Найти степень истинности высказывания

R = (PÚQ) « (P® (PÙQ)) при P= 0,9; Q = 0,3.

1. PÙQ = min(0,9; 0,3) = 0,3.

2. (P® (PÙQ)) = max (1 – 0,9; 0,3) = 0,3.

3. PÚQ = max (0,9; 0,3) = 0,9.

4. R = min (max (1 – 0,9; 0,3), max (0,9; 1 – 0,3)) = min(0,3; 0,9) = 0,3.

Множество нечетких высказываний вместе с введенными на них операциями образуют алгебру нечетких высказываний.

Нечеткой логической формулой называется:

1) любая нечеткая высказывательная переменная;

2) если P и Q – нечеткие логические формулы, то ØP, PÙQ, PÚQ, P®Q, P« Q – тоже нечеткие логические формулы;

3) других формул, кроме построенных по правилам двух предыдущих пунктов, нет.

Пусть P(X₁, X₂, …,X_n) и Q(X₁, X₂, …,X_n) – две нечеткие логические формулы. Степенью равносильности формул P и Q называется величина

m(P, Q) = 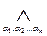{ P(a₁, a₂, …,a_n) « Q(a₁, a₂, …,a_n)}

Здесь логические операции конъюнкции и эквивалентности имеют смысл, определенный для логических операций над нечеткими высказываниями, причем конъюнкция берется по всем наборам степеней истинности (a₁, a₂, …,a_n) нечетких переменных (X₁, X₂, …,X_n).

Если m(P, Q) = 0,5, то нечеткие формулы P и Q называются индифферентными.

Если m(P, Q) > 0,5, то нечеткие формулы P и Q называются нечетко равносильными.

Если m(P, Q) < 0,5, то нечеткие формулы P и Q называются нечетко неравносильными.

Степенью неравносильности формул P и Q называется величина

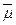(P, Q) = 1 – m(P, Q) .

Пример 4.2.

Определить степень равносильности формул.

P = X® Y, Q= Ø(XÙ Y) при условии, что X и Y принимают значения степеней истинности из множества {0,1; 0,3}. Перечислим все возможные наборы значений X и Y:

A₁ = {0,1; 0,1}; A₂ = {0,1; 0,3}; A₃ = {0,3; 0,1}; A₄ = {0,3; 0,3}.

Запишем формулы P и Q с учетом определений логических операций:

P = X® Y = max (1 –X, Y); Q =Ø(XÙ Y) = 1 – XÙY = 1 – min(X, Y).

Вычислим формулы P и Q на каждом из четырех наборов A₁ – A₄:

P1 = max (1 – 0,1; 0.1) = 0,9. P2 = max (1 – 0,1; 0,3) = 0,9. P3 = max (1 – 0,3; 0,1) = 0,7. P4 = max (1 – 0,3; 0,3) = 0,7.

Q1 = 1 – min( 0,1; 0.1) = 0,9. Q2 = 1 – min(0,1; 0,3) = 0,9. Q3 = 1 – min(0,3; 0,1) = 0,9. Q4 = 1 – min (0,3; 0,3) = 0,7.

Вычислим теперь степень равносильности формул P и Q. Для этого сначала вычислим P(a₁, a₂, …,a_n) « Q(a₁, a₂, …,a_n) для всех наборов A₁ – A₄:

P« Q = min (max (1 –P, Q), max (P, 1 – Q)).

Поэтому

P₁« Q₁ = min (max (1 – 0,9;0,9), max (0,9; 1 –0,9)) = 0,9.

P₂« Q₂ = min (max (1 – 0,9;0,9), max (0,9; 1 –0,9)) = 0,9.

P₃« Q₃ = min (max (1 – 0,7;0,9), max (0,7; 1 –0,9)) = 0,7.

P₄« Q₄ = min (max (1 – 0,7;0,8), max (0,7; 1 –0,7)) = 0,7.

Окончательно получим

m(P, Q) = 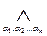{P(a₁, a₂, …,a_n) « Q(a₁, a₂, …,a_n)} = 0,9Ù0,9Ù0,7Ù0,7 = min(0,9; 0,9; 0,7; 0,7) = 0,7.

Формулы P и Q нечетко равносильны.

На других наборах степеней истинности нечетких переменных X и Y формулы P и Q могут быть нечетко неравносильны.

Задания

Определить степень равносильности формул P и Q при условии, что X и Y принимают значения степеней истинности из множества {0,1; 0,5}.

Варианты индивидуальных заданий

№	P	Q	№	P	Q
	X ÙØ Y	X ®ØY		ØX Ú Y	X ÙØ Y
	ØX Ú Y	X ® Y		X ® Y	ØX Ú Y
	X ®ØY	X ÙØ Y		X ÙØ Y	X ®ØY
	X Ù Y	X Ú ØY		X ®ØY	X Ù Y
	X Ú ØY	ØX Ù Y		ØX Ù Y	X Ú ØY
	X ® Y	ØX Ú Y		X Ú ØY	X ® Y
	ØX ® Y	Y ® X		Y ® X	ØX ® Y
	Y ®Ø X	ØX ® Y		ØX ® Y	Y ®Ø X
	ØY ® X	Y ®ØX		Y ®ØX	ØY ® X
	ØY ®Ø X	Y ® X		Y ® X	ØY ®Ø X