Упражнения. 4.1.1. Установите соответствие между формой передачи информации, средствами передачи и каналам связи в зависимости от степени развития общества и

4.1.1. Установите соответствие между формой передачи информации, средствами передачи и каналам связи в зависимости от степени развития общества и индивидуальных возможностей людей. Заполните табл. 6.11, выбрав из предложенных, а также добавив:

Период	Средства связи передачи информации	Форма передачи (вид сигнала)	Сигналы, с помощью которых передается
Первобытное общество
Средние века
Современное общество

Табл.6.11

Средства передачи информации: костер, барабан, слово, книга, телефон, радио, телеграф, телевизор, почтовый голубь, электронная почта, факс и другое.

4.1.2.Переведите число из десятичной в двоичную, восьмеричную и шестнадцатеричную системы счисления:

а) 43	б) 66	в) 76	г) 89	д) 98
е) 57	ж) 63	з) 24	и)74	к) 40

Образец: Переведите число 52 из десятичной в двоичную, восьмеричную и шестнадцатеричную системы счисления:

Решение: 1) при делении числа 52 на q=2 имеем двоичное число, записанное от старшего разряда к младшему 52₁₀=110100₂;

2) при делении числа 52 на q=8 имеем восьмеричное число, записанное от старшего разряда к младшему 52₁₀=64₈;

3) при делении числа 52 на q=16 имеем восьмеричное число, записанное от старшего разряда к младшему 52₁₀=34₁₆.

4.1.3. Переведите двоичное число в десятичную, восьмеричную и шестнадцатеричную системы счисления:

а) 10011010	б) 10111011	в) 01010001	г) 01011101	д) 11010100
е) 01001010	ж) 11010011	з)01001100	и) 01010110	к) 01110111

Образец: Переведите двоичное число 10001110₂ в десятичную, восьмеричную и шестнадцатеричную систему счисления.

Решение: 1) Представим 10001110₂ в виде суммы разложений по степеням числа 2. Имеем .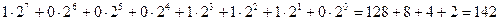

2) Для перевода в восьмеричную и шестнадцатеричную системы счисления можно воспользоваться общей таблицей перевода. Разобъем двоичное число 10001110₂ на тетры – четверки. Имеем кортежи 1000 и 1110. Запишем в таблице соответствие этих двоичных четверок как восьмеричным, так и шестнадцатеричным числам:

Системы счисления	Заданные числа
«2»
«8»
«16»		Е
«10»

Отсюда 10001110₂=1016₈=8E₁₆

4.1.4. Переведите шестнадцатеричное число в двоичную, восьмеричную и десятичную системы счисления числа:

Образец: Перевести шестнадцатеричное число F5₁₆ в двоичную систему счисления.

Решение: Установим соответствие между шестнадцатеричными числами и их представлениями в иных системах счисления по таблиц. Имеем:

Системы счисления	Заданные числа
«16»	F
«2»
«8»
«10»

Тогда F5₁₆=1110101₂ =1705₈=155₁₀.

4.1.5. Найдите сумму, разность и произведение чисел А и В в двоичной системе счисления и сделайте проверку результата в десятичной системе счисления:

а)	А=100110, В=101000	б)	А=010111, В=010010	в)	А=011011 В=110000	г)	А=101100 В=001001	д)	А=111010 В=101000
е)	А=110011 В=001001	ж)	А=010011 В=110010	з)	А=010110 В=011010	и)	А=110111 В=010110	к)	А=010101 В=010011

Образец: Найдите сумму, разность и произведение чисел А и В в двоичной системе счисления. Пусть А=011110 и В=011011

1) Найдем сумму А + В и разность А – В.

Решение: Имеем:

011110 011110

+ –

011011 011011

111001 000011

4.1.6.Выполните сложение и вычитание чисел в восьмеричной системе счисления, и проверить результат, сложив эти же числа, переведенные в десятичную систему счисления:

а)	А8=53472 В8=43576	б)	А8=32047 В8=25743	в)	А8=45206 В8=47345	г)	А8=64205 В8=25706	д)	А8=30657 В8=154757
е)	А8=267054 В8=12476	ж)	А8=15206 В8=42345	з)	А8=35206 В8=47315	и)	А8=15206 В8=47325	к)	А8=75206 В8=47145

Образец: А₈=58421 В₈=23574

Решение:

4.1.7. Выполните сложение и вычитание в шестнадцатеричной системе счисления и сделайте проверку в десятичной:

а)	А16=C38964 B16=C9A538	б)	А16=F79832 B16=5AB63	в)	А16=87FDC B16=5ADF7	г)	А16=987F4 B16=A74F5	д)	А16=B4599 B16=845FA3
е)	А16=D5B6C B16=B7AF8	ж)	А16=C38974 B16=C2A538	з)	А16=F798С2 B16=В74F1	и)	А16=B459Е B16=645FA3	к)	А16=37FDC B16=5A0F7

Образец: А₁₆=А38Е64 В₁₆=F7В8А2

Решение

4.1.8. В какой системе счисления х возможно равенство:

а) 410=(10)x	б) 810=(11)x	в) 910=(100)x	г) 2610=(31)x	д) 2310=(17)x
е) 4210=(52)x	ж) 19310=(301) x	з) 15310=(603) x	и) 61210=(507) x	к) 44010 = (308) x

Образец: 401₁₀=(809) _x

Решение: 1)Представим число 809 разложенным по степеням основания x.

Тогда число 809 примет вид: (809) _x = .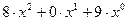

2) Составим и решим уравнение:

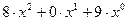=401. Отсюда x=7. Т.о., заданное равенство возможно в семеричной системе счисления.

…