Законы раскрытия импликации

Логические равносильности (ЛР)

ЛР нельзя доказать в рамках привычной нам алгебры действительных чисел, но они легко доказываются с помощью таблиц истинности.

Пусть 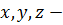произвольные высказывания. Обозначим 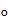переменную с областью значений { }.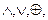

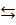Закон коммутативности:

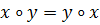
Это соотношение означает выполнение коммутативности для любой из операций 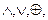, входящих в область значений переменной .

Закон ассоциативности:

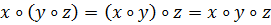
Свойство ассоциативности позволяет рассматривать составные высказывания, состоящие из трех и более простых высказываний. Это один из важнейших логических законов, широко используемый в преобразованиях.

Обозначим далее через 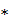(читается «звездочка») переменную с областью значений { 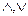}, а через 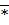(читается «звездочка с чертой») – зависимую от нее переменную, задаваемую следующим образом:

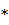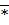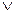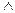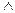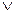Законы дистрибутивности:

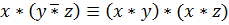
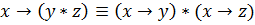
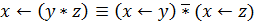
Последнюю равносильность правильнее было бы назвать законом квазидистрибутивности, так как слева стоит 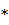, а справа .

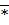Законы поглощения:

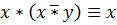
x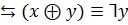

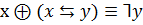
закон де Моргана:

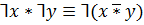
Закон вычеркивания:

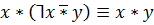
Закон выявления

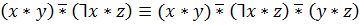
Закон идемпотентности

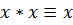
Закон двойного отрицания

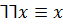
Законы противоречия

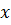
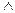
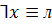(или 0)

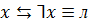(или 0)

Закон исключенного третьего

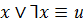(или 1)

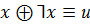(или 1)

Закон сокращения посылки

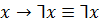
Законы получения констант

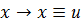
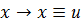
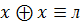
Законы подстановки констант

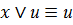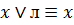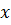
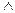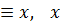
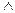, , и л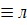

,

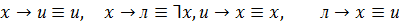
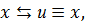
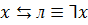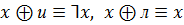
Закон контрапозиции

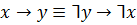
Закон приведения к противоречию

Пусть 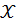– высказывательная переменная с областью значений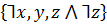

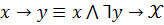
Закон объединения посылок

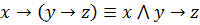
Закон зачеркивания посылки

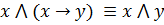
Закон раскрытия эквивалентности

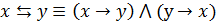
Закон четности эквивалентности

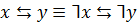
Законы раскрытия импликации

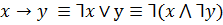
Комментарий к законам равносильностей: дистрибутивность обычно используется в виде 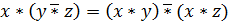, причем для тождественных преобразований чаще применяется антидистрибутивность, то есть вынесение логических переменных за скобки. Другие формы закона дистрибутивности, как правило, не используются.

Законы поглощения и де Моргана одни из самых важных равносильностей. Преобразование де Моргана обычно применяется вместе с законом отрицания отрицания.

Например,
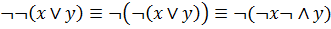и в другую сторону. Таким путем отрицание можно перенести на переменные. Очень часто используются равносильности, связанные с импликацией (кроме вычеркивания). Законы идемпотентности, подстановки и получения констант – простые и очевидные – применяются всегда.

Законы математической логики (МЛ) используются для упрощения формул, для доказательства тождественной истинности или ложности, для установления равносильности правой и левой части формул и т.д.

Пример:

Упростить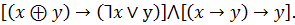

Такие задачи часто решаются при конструировании электронных схем.

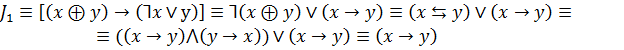
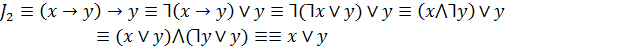
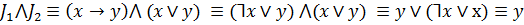
Варианты заданий для раздела «Логика»

1. Приведите пример составного высказывания, которое можно было бы записать в следующем виде и определите его истинностное значение (с помощью таблицы истинности)

1). (A→B)∨(C∧B);	16). (A∧B)∨(C∧B);
2).(A→B)↔(C∧B);	17). (A↔B)∧(C∨B);
3).(A∨(C∧B);	18). (A→B)∨(C→B);
4). B∨(C→(B∧A));	19). (A∧(B→C))↔B;
5).(A↔B)∨(C↔B);	20). (A→B)→(C→B);
6). (A→B)∨ (C∧B);	21). (A∧B)→(C∧B);
7). (A∨(C→B))↔B;	22). (A∨B∨C)→(C∧B);
8). (A→B)↔ (C∨B);	23). (A∧B∧C)∨(C∧B);
9). (A→B)∨(C→B);	24). (A→B)∨(C→B)
10). B∨(A→(C∧B));	25). (A∧B∧C)↔(C∧B);
11). B∨(A→(C∧B));	26). (A↔B)→(C↔B);
12). B↔(A→(C∧B));	27). (A∨B)→(C∨B);
13). (A∧(C→B))↔B;	28). (A∨B)→(C∧B);
14). (A∨(C↔B));	29). ((A∨B)↔C)∧B;
15). (C∨B)∧(A↔B);	30). (A∨B)∧(C∨B).

2. С помощью равносильных преобразований упростите формулу и проверьте результат с помощью таблицы истинности:

1). (X∧(X∨Y))∨(X∨(X∧Y))≡

2).(X∨Y)∧(X∧Y)≡

3).(X→ Y)∨(X∧(X∨Y))≡

4).(X→X)∧(X∧(X∨Y))≡

5).(X∧(X∨Y))∨(X∧(X∨Y))≡

3. Приведите формулы и докажите логические равносильности:

1). законы коммутативности	11). законы вычеркивания
2). закон ассоциативности	12). законы выявления
3). законы дистрибутивности	13). законы идемпотентности
4). законы поглощения	14). законы противоречия
5). законы де Моргана	15). закон исключенного третьего
6).закон сокращения посылки	16).законы получения констант
7).законы подстановки констант	17). закон контрапозиции
8). закон объединения посылок	18). закон зачеркивания посылки
9).закон раскрытия эквивалент-ности	19). закон четности эквивалент-ности
10). законы раскрытия импликации	20). закон двойного отрицания