Примеры бинарных отношений. 5 страница
Пример. Пусть заданы множества 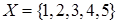 ,
, 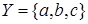 и отношения на них
и отношения на них 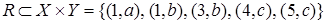 ,
, 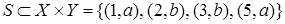 .
.
Тогда 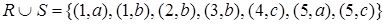 ;
; 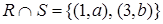 ;
; 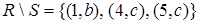 ;
; 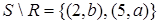 ;
;
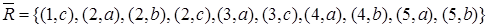 ;
;
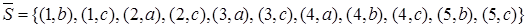 .
.
Пример операции сечения отношений приведен выше.
Рассмотрим операцию обращения (симметризации) отношений.
Определение
Отношение, симметричное (обратное) некоторому отношению 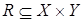 , обозначается
, обозначается 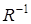 и представляет собой подмножество множества
и представляет собой подмножество множества 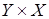 , образованное теми парами
, образованное теми парами 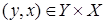 , для которых
, для которых 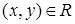 .
.
Если 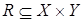 , то
, то 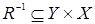 , если
, если 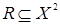 , то
, то 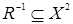 .
.
Переход от  к
к 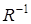 осуществляется взаимной перестановкой координат каждой упорядоченной пары.
осуществляется взаимной перестановкой координат каждой упорядоченной пары.
Пример.Отношение  - «
- «  делитель
делитель  », а обратное к нему
», а обратное к нему 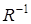 - «
- «  кратно
кратно  ».
».
Пусть 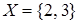 ,
, 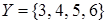 и
и  отношение «быть делителем» от
отношение «быть делителем» от  к
к  . Тогда
. Тогда 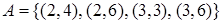 и
и 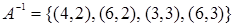 .
.
При переходе от  к
к 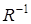 область определения становится областью значений и наоборот. Матрица
область определения становится областью значений и наоборот. Матрица 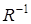 - транспонированная матрица отношения
- транспонированная матрица отношения  . Граф обратного отношения находится из исходного графа заменой направлений всех дуг на противоположные.
. Граф обратного отношения находится из исходного графа заменой направлений всех дуг на противоположные.
Рассмотрим операцию композиции отношений, которая позволяет получить отношение из двух других отношений.
Пусть даны три множества 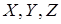 и два отношения
и два отношения 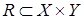 и
и 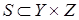 .
.
Определение
Композиция отношений  и
и  есть отношение
есть отношение 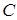 , состоящее из всех тех пар
, состоящее из всех тех пар 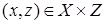 , для которых существует такое
, для которых существует такое 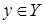 , что
, что 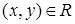 и
и 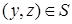 .
.
Композиция 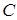 отношений
отношений  и
и  обычно обозначается как
обычно обозначается как 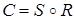 (или
(или 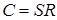 ).
).
Пример. Пусть заданыдва отношения:
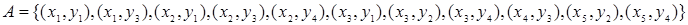 и
и 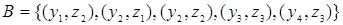 .
.
Очевидно, что композиция 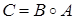 будет представлена следующим образом
будет представлена следующим образом
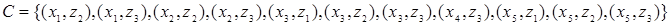
Композиция отношений имеет следующие свойства:
- 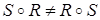 , т.е. закон коммутативности не выполняется;
, т.е. закон коммутативности не выполняется;
- 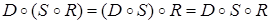 , т.е. закон ассоциативности выполняется;
, т.е. закон ассоциативности выполняется;
- 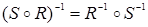 ;
;
- 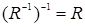 .
.
Композиция отношений 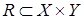 и
и 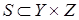 , где
, где 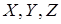 - множества, наглядно представляется с помощью графов. Прежде всего, необходимо к графу отношения
- множества, наглядно представляется с помощью графов. Прежде всего, необходимо к графу отношения  достроить граф отношения
достроить граф отношения  . Граф отношения
. Граф отношения 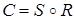 может быть получен при исключении вершин, соответствующих элементам множества
может быть получен при исключении вершин, соответствующих элементам множества  . При исключении вершины
. При исключении вершины 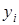 каждый проходящий через неё путь от вершин
каждый проходящий через неё путь от вершин 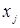 к вершинам
к вершинам 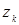 заменяется одной дугой с тем же направлением. Параллельные ветви с одинаковыми направлениями соответствуют одинаковым парам в
заменяется одной дугой с тем же направлением. Параллельные ветви с одинаковыми направлениями соответствуют одинаковым парам в 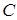 и рассматриваются как одна ветвь.
и рассматриваются как одна ветвь.
Пример. Пусть заданы множества 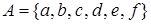 ,
, 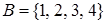 и
и 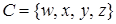 , а также отношения
, а также отношения 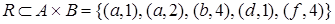 и
и 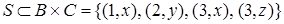 . Построим отношение
. Построим отношение 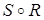 .
.
Построим граф отношения  и достроим к нему граф отношения
и достроим к нему граф отношения  (рис. 3.6).
(рис. 3.6).
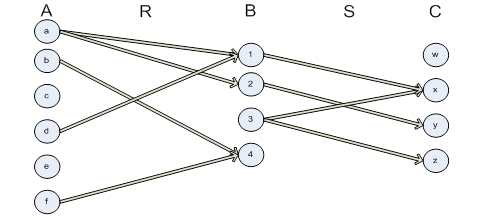
Рисунок 3.6 - Граф отношения  и отношения
и отношения 
Исключим вершины 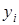 и каждый проходящий через неё путь от вершин
и каждый проходящий через неё путь от вершин 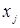 к вершинам
к вершинам 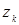 заменим одной дугой с тем же направлением, получим граф отношения
заменим одной дугой с тем же направлением, получим граф отношения 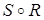 (рис. 3.7).
(рис. 3.7).

Рисунок 3.7 - Граф отношения 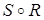
Аналогично можно получить матрицу композиции 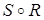 как произведение матриц отношений
как произведение матриц отношений  и
и  (в порядке их следования), которое выполняется по обычному правилу умножения прямоугольных матриц с последующей заменой отличного от нуля элемента результирующей матрицы единицей.
(в порядке их следования), которое выполняется по обычному правилу умножения прямоугольных матриц с последующей заменой отличного от нуля элемента результирующей матрицы единицей.
3.6 Контрольные вопросы и задания
1. Как связаны между собой теория множеств и теория отношений?
2. Поясните понятие кортежа. Приведите примеры кортежей.
3. Что такое прямое (декартово) произведение множеств?
4. Как определяется мощность декартового произведения?
5. Что такое отношение множеств?
6. Какое отношение называется  -арным, унарным, бинарным?
-арным, унарным, бинарным?
7. Что такое тождественное отношение, полное отношение, нулевое отношение?
8. Пусть  - некоторое множество. Что означает запись
- некоторое множество. Что означает запись 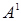 ,
, 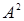 ,
, 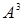 ,
, 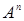 ?
?
9. Что является областью определения и областью значения отношения  ?
?
10. Назовите способы задания отношений.
11. Какие из способов задания отношений применимы для  -арных отношений при
-арных отношений при 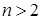 ?
?
12. Перечислите операции, производимые над отношениями.
13. Дайте определение сечения отношения  по элементу
по элементу 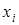 .
.
14. Что такое фактор-множество множества  по отношению
по отношению  ?
?
15. Назовите специфические операции над отношениями.
16. Что такое композиция отношений?
17. Что такое симметризация отношений?
18. Какое отношение называется обратным?
Лекция 4 Свойства бинарных отношений
4.1 Основные свойства бинарных отношений
Отношения могут обладать некоторыми общими свойствами (например, отношение включения и отношение равенства транзитивны). Определяя эти свойства и комбинируя их, можно выделить важные типы отношений, изучение которых в общем виде заменяет рассмотрение огромного множества частных отношений.
Пусть  - бинарное отношение в множестве
- бинарное отношение в множестве 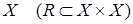 . Определим общие свойства таких отношений, которые должны выполняться для всех
. Определим общие свойства таких отношений, которые должны выполняться для всех 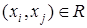 :
:
- рефлексивность;
- антирефлексивность;
- симметричность;
- асимметричность;
- антисимметричность;
- транзитивность;
- антитранзитивность.
Определение. Отношение 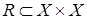 называется рефлексивным, если
называется рефлексивным, если 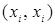 принадлежит
принадлежит  для всех
для всех 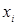 из
из  , т.е. оно всегда выполняется между объектом и им самим (
, т.е. оно всегда выполняется между объектом и им самим ( 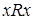 ).
).
Для рефлексивного отношения все элементы матрицы на главной диагонали равны 1. Граф рефлексивного отношения содержит петли у всех вершин.
Определение. Отношение 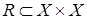 называется антирефлексивным, если
называется антирефлексивным, если 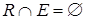 (
( 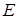 - тождественное отношение), т.е. может выполняться только для несовпадающих объектов: из
- тождественное отношение), т.е. может выполняться только для несовпадающих объектов: из 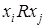 следует
следует 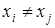 .
.
Для антирефлексивного отношения все элементы матрицы на главной диагонали равны 0. Граф антирефлексивного отношения не содержит петель у вершин, нет дуг вида 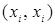 .
.
Примеры.
Отношение равенства («=»), отношение « 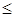 » на множестве вещественных чисел, отношение «иметь общий делитель» на множестве целых чисел рефлексивны.
» на множестве вещественных чисел, отношение «иметь общий делитель» на множестве целых чисел рефлексивны.
Отношение « 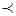 » на множестве вещественных чисел, отношения «быть сыном», «быть старше» на множестве людей антирефлексивны.
» на множестве вещественных чисел, отношения «быть сыном», «быть старше» на множестве людей антирефлексивны.
Отношение «быть симметричным относительно оси  на множестве точек координатной плоскости» не является ни рефлексивным, ни антирефлексивным: точка плоскости симметрична сама себе, если она лежит на оси
на множестве точек координатной плоскости» не является ни рефлексивным, ни антирефлексивным: точка плоскости симметрична сама себе, если она лежит на оси  , и несимметрична сама себе в противном случае.
, и несимметрична сама себе в противном случае.
Определение. Отношение 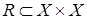 называется симметричным, если
называется симметричным, если 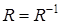 , т.е. при выполнении соотношения
, т.е. при выполнении соотношения 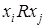 выполняется и соотношение
выполняется и соотношение 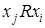 (
(  выполняется либо в обе стороны, либо не выполняется вообще).
выполняется либо в обе стороны, либо не выполняется вообще).
Симметричность отношения влечет и симметричность матрицы.
Для симметричного отношения вершины графа могут быть связаны только парами противоположно направленных дуг (ненаправленными ребрами).
Определение. Отношение 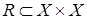 называется асимметричным, если
называется асимметричным, если 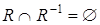 , т.е. из двух соотношений
, т.е. из двух соотношений 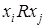 и
и 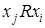 по меньшей мере одно не выполняется. Если отношение асимметрично, то оно и антирефлексивно.
по меньшей мере одно не выполняется. Если отношение асимметрично, то оно и антирефлексивно.
Матрица асимметричного отношения характеризуется тем, что у неё нулевые элементы на главной диагонали и нет ни одной пары единиц, стоящих на симметричных относительно главной диагонали местах (несимметричность матрицы).
В графе асимметричного отношения петли отсутствуют, а вершины могут быть связаны только одной направленной дугой.
Определение. Отношение 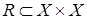 называется антисимметричным, если
называется антисимметричным, если 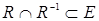 (
( 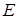 - тождественное отношение), т.е. оба соотношения
- тождественное отношение), т.е. оба соотношения 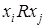 и
и 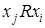 выполняются одновременно только тогда, когда
выполняются одновременно только тогда, когда 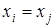
Матрица антисимметричного отношения является несимметричной, но на главной диагонали могут находиться как 0, так и 1.
В случае антисимметричного отношения в графе могут быть петли, но связь между вершинами, если она имеется, отображается только одной направленной дугой.
Пример. Расстояние между двумя точками на плоскости, отношение «быть братом» в множестве людей являются примерами симметричного отношения.
Отношение строгого включения в множестве всех подмножеств некоторого универсума и отношение «быть отцом» в множестве людей являются асимметричными.
Отношение нестрогого включения в множестве всех подмножеств некоторого универсума, отношения нестрогого неравенства « 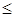 » и «
» и « 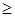 » на множестве целых, действительных чисел являются антисимметричными.
» на множестве целых, действительных чисел являются антисимметричными.
Определение.Отношение 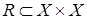 называется
называется  транзитивным, если
транзитивным, если 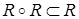 , т.е. из
, т.е. из 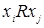 и
и 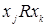 следует
следует 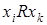 .
.
В матрице транзитивного отношения для каждой пары единичных элементов, один из которых расположен в 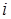 -й строке и
-й строке и 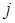 -м столбце, а другой в
-м столбце, а другой в 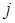 -й строке и
-й строке и  -м столбце, обязательно существует единичный элемент, расположенный в клетке на пересечении
-м столбце, обязательно существует единичный элемент, расположенный в клетке на пересечении 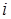 -й строки и
-й строки и  -ого столбца (наличие единичных элементов на главной диагонали не нарушает транзитивности).
-ого столбца (наличие единичных элементов на главной диагонали не нарушает транзитивности).
Наглядно проявляется на графе свойства транзитивности: если через некоторую совокупность вершин графа проходит путь, то существуют дуги, соединяющие любую пару вершин из этой совокупности. Обычно в графе транзитивного отношения изображают только этот путь, а обусловленные транзитивностью дуги опускают. Такой упрощенный граф называют графом редукции.
Определение.Отношение 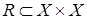 называется
называется  антитранзитивным, если из
антитранзитивным, если из 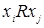 и
и 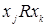 следует, что не выполняется
следует, что не выполняется 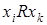 .
.
Примеры. Отношения «равенство», «быть делителем», заданные на множестве целых чисел, и отношение «жить в одном городе», заданное на множестве людей являются транзитивными.
Отношение «быть сыном» на множестве людей является антитранзитивным.
4.2 Классы бинарных отношений
4.2.1 Отношение эквивалентности
Отношение эквивалентности представляет собой экспликацию (перевод интуитивных представлений в ранг строгих математических понятий) таких обыденных слов как «одинаковость», «неразличимость», «взаимозаменяемость».
Определение. Бинарное отношение в множестве  называется отношением эквивалентности (обозначается ~), если для него выполняются следующие свойства:
называется отношением эквивалентности (обозначается ~), если для него выполняются следующие свойства:
- рефлексивность ( 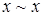 );
);
- симметричность (если 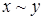 , то
, то 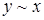 );
);
- транзитивность (из ) 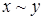 и
и 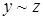 следует
следует 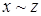 .
.
Примеры отношений эквивалентности:
- «проживать в одном доме » в множестве людей;
- «подобие треугольников» в множестве всех треугольников на плоскости;
- «параллельность прямых» в множестве всех прямых на плоскости.
Важнейшее значение эквивалентности состоит в том, что это отношение определяет признак, который допускает разбиение множества  на непересекающиеся подмножества
на непересекающиеся подмножества 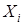 , называемые классами эквивалентности. Наоборот, всякое разбиение множества
, называемые классами эквивалентности. Наоборот, всякое разбиение множества  на непересекающиеся подмножества определяет между элементами этого множества некоторое отношение эквивалентности.
на непересекающиеся подмножества определяет между элементами этого множества некоторое отношение эквивалентности.
Теорема 4.1
Если на множестве  задано отношение эквивалентности, то это отношение задает разбиение множества и это разбиение единственно.
задано отношение эквивалентности, то это отношение задает разбиение множества и это разбиение единственно.
Все элементы, принадлежащие некоторому классу 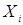 разбиения
разбиения 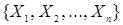 множества
множества  , связаны между собой отношением эквивалентности. Они взаимозаменяемы в том смысле, что любой из этих элементов определяет данный класс, т.е. может служить его представителем (эталоном). Каждый класс отождествляется с некоторым общим свойством или совокупностью свойств (параметров) входящих в него элементов.
, связаны между собой отношением эквивалентности. Они взаимозаменяемы в том смысле, что любой из этих элементов определяет данный класс, т.е. может служить его представителем (эталоном). Каждый класс отождествляется с некоторым общим свойством или совокупностью свойств (параметров) входящих в него элементов.
Подмножество из  , содержащее по одному и только одному элементу из каждого класса некоторого разбиения, называют системой представителей соответствующего отношения эквивалентности. Множество всех классов разбиения множества
, содержащее по одному и только одному элементу из каждого класса некоторого разбиения, называют системой представителей соответствующего отношения эквивалентности. Множество всех классов разбиения множества  , определяемого отношением эквивалентности
, определяемого отношением эквивалентности  , образует фактор-множество
, образует фактор-множество 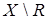 .
.
Предельным случаем отношения эквивалентности является тождественное равенство. Единственный элемент, равный какому-либо данному элементу, есть этот самый элемент. Следовательно, имеем самое полное разбиение, при котором классы эквивалентности содержат только по одному элементу исходного множества.
Пример. Отношение «проживать» в множестве жителей города является эквивалентностью и разбивает это множество на непересекающиеся подмножества людей, являющихся соседями по дому.
Пример. Отношение параллельности определяет разбиение множества прямых на плоскости на классы, каждый из которых образован множеством параллельных между собой прямых и характеризуется некоторым направлением (следует также считать, что прямая параллельна самой себе). Любая из параллельных прямых может служить представителем данного класса, а само направление есть класс эквивалентности. Множество всех направлений составляет фактор-множество множества всех прямых по отношению параллельности.
Элементы, принадлежащие одному классу эквивалентности, попарно эквивалентны между собой, следовательно, столбцы матрицы отношения эквивалентности для элементов одного класса эквивалентности одинаковы и содержат единицы во всех строках, которые соответствуют этим элементам. Так как классы эквивалентности не пересекаются, то в столбцах, соответствующих элементам различных классов, не будет единиц в одних и тех же строках.
При построении матрицы отношения расположим элементы множества так, чтобы элементы, принадлежащие одному классу эквивалентности, стояли рядом. Тогда единичные элементы матрицы отношения эквивалентности образуют непересекающиеся квадраты, диагонали которых располагаются на главной диагонали матрицы.
ПримерДля отношения эквивалентности, заданного классами эквивалентности 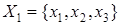 ;
; 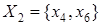 ;
; 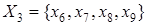 , матрица будет иметь вид
, матрица будет иметь вид
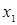 |  | 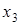 | 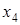 | 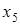 | 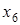 | 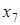 | 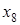 | 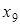 | |
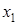 | |||||||||
 | |||||||||
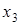 | |||||||||
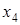 | |||||||||
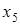 | |||||||||
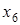 | |||||||||
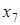 | |||||||||
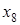 | |||||||||
 |
