Реалізація цифрових автоматів на ПЛІС ALTERA DE-2

З дисципліни

“Програмовані логічні схеми”

Для студентів спеціальності

“Телекомунікації та радіотехніка”,

Спеціалізації

“Радіоелектронні апарати та засоби”

Тема курсового проекту

“Реалізація цифрового автомата на ПЛІС”

Завдання для курсового проекту:

Реалізувати цифровий автомат Мілі (Мура) на програмованій логічній схемі з використанням плати Altera DE2 за заданими таблицями переходів та виходів автомата

Теоретичні відомості

Загальна характеристика автоматів

Цифровий автомат покроково перетворює дискретну інформацію в дискретні інтервали часу. На вході і виході автомата можуть бути символи, слова або вирази будь-якої мови, що представляють собою елемент дискретної інформації. Перетворення елементів вхідної інформації в елементи вихідної інформації виконується за заданим алгоритмом.

Робота ЦА здійснюється в режимі автоматного часу, визначеного частотою надходження вхідних сигналів.

Класифікація автоматів

Всі автомати можна класифікувати за такими ознаками:

1) за ступенем розкриття структури автомати бувають:

• абстрактні автомати (автомати, деталі структури яких не розкриті, розглядають загальні питання побудови автоматів, не враховуючи їх фізичну природу);

• структурні автомати (розкриті деталі структури, враховують технічну реалізацію автоматів, елементну базу, форму сигналів).

2) за скінченними множинами X (множина вхідних сигналів ), Y (множина вихідних сигналів) і S (множина станів) або за кількістю елементів в алфавіті опису автомати бувають - скінченними і нескінченними.

ЦА вважається скінченним, якщо скінченні множини вхідних сигналів X, станів S і вихідних сигналів Y.

3) за обсягом пам'яті автомати поділяються на автомати:

• з пам'яттю (послідовні автомати);

• автомати без пам'яті (логічні комбінаційні схеми) або комбінаційні автомати.

Функціональним вузлом послідовного автомата або автомата з пам'яттю являється пристрій, логічна функція якого визначається не тільки набором вхідних сигналів на даному такті, але і значенням цієї функції на попередньому такті, тобто вхідною змінною є і попереднє значення самої функції. Yn = f( x1, x2, .... xn, Yn -1).

Комбінаційний автомат - автомат в якому значення вихідний функції Yt в перебігу кожного такту визначається набором вхідних аргументів X1, X2, ... Xt. В іншому випадку комбінаційний автомат зберігає сигнал на виході до тих пір, поки на вході є комбінація певних сигналів.

4) за законом функціонування, або за виглядом вихідної функції ЦА поділяються на:

• автомати 1 -го роду (автомати Мілі);

• автомати 2 -го роду (автомати Мура).

Розглянемо оператори формування автоматів першого роду (автомата Мілі):

s(t) = d(s(t-1), x(t));

y(t) = l(s(t-1), x(t)).

де s(t) - стан автомата в даний момент,

s(t-1) - стан автомата в попередній момент. Якщо t = 0, то s(t-1) = s₀,

x(t) - вхідний сигнал у поточний момент,

d- оператор формування даного стану s,

λ - оператор формування даного вихідного сигналу y.

Як бачимо, закон функціонування являє собою сукупність двох функцій: функції переходу d і функції виходу λ.

Очевидно, що даний стан s(t) залежить від попереднього стану s(t-1) і вхідного сигналу в даний момент часу. Вихідний сигнал в даний момент часу так само визначається попереднім станом і вхідним сигналом в даний момент часу (рис. 1).

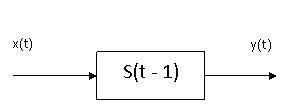
Рис. 1. Схема цифрового автомата

Функція виходу ЦА 2-го роду відрізняється від такої ж функції ЦА 1-го роду тим, що використовується позиція в даний момент часу s(t). Таким чином, закон функціонування ЦА 2-го роду є наступним:

s(t) = d(s(t-1), x(t)),

y(t) = l(s(t), x(t)).

5) за повнотою використовуваних переходів автомати поділяються на

• повністю визначені автомати;

• частково визначені автомати (автомат, у якого функції виходу і переходу визначені не повністю).

6) по стабільності періоду проходження вхідних сигналів автомати бувають:

• синхронні автомати (період проходження вхідних сигналів - постійна величина. Перемикання стану відбувається в строго певні моменти часу (не пов'язано з часом закінчення операції);

• асинхронні автомати (період тривалості тактів – не постійна величина. Момент перемикання стану визначається моментом завершення операції);

7) за імовірністю переходів автомати поділяються на:

• детерміновані (не імовірнісні);

• не детерміновані (імовірнісні) автомати.

Якщо функції виходів і переходів є випадковими, то автомат - недетермінованний або імовірнісний.

8) за відношеннями між автоматами серед автоматів можна виділити

• підавтомати;

• надавтомати.

Якщо, наприклад, відомо, що ЦА (А) < ЦА (В), то автомат А є підавтоматом автомата В, а автомат В - надавтоматом автомата А;

9) при нульовій потужності множини внутрішніх станів (|S| = 0) автомат називається автономним, при |Y| = 0 - автоматом без виходу;

10) за функціями виконання - керуючі і виконуючі (операційні) автомати.

Операційний автомат (ОА) служить для виконання власне набору необхідних операцій алгоритму. Керуючий автомат задає послідовність дій за алгоритмом залежно від умов (які також формуються ОА у вигляді логічних сигналів), тобто координує дії вузлів ОА. Він видає в деякій часовій послідовності керуючі сигнали, під дією яких у вузлах ОА виконуються необхідні дії, наприклад, установка регістра в певний стан, інвертування вмісту розрядів регістра, пересилання вмісту одного вузла в інший, зсув вмісту сайту вліво, вправо, рахунок, при якому число в лічильнику (регістрі) збільшується або зменшується на одиницю, додавання і т. д.

Загальне зображення, наприклад, ЦА зображено на рис. 1.2.

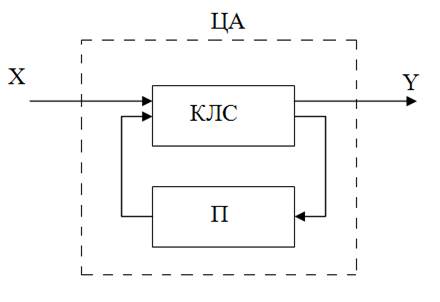
Рис. 2. Структурна схема ЦА

Будь-який ЦА складається з двох частин: комбінаційної логічної схеми (КЛС) і пам'яті (П).

У даному випадку в деякій мірі розкрита структура автомата.

• КЛС автомата формує вихідні сигнали, сигнали переходу тригерів блоку пам'яті в нові стани.

• Наявність блоку пам'яті дозволяє зберегти передісторію роботи автомата під дією вхідних сигналів.

Особливою відмінністю автоматів Мілі є те, що їх вихідні сигнали залежать як від стану автомата, так і від значення вхідного сигналу. В автоматах Мура вихідні сигнали y(t) у кожний дискретний момент часу t однозначно визначаються станом автомата в той же момент часу і не залежать від значення вхідного сигналу.

Абстрактні автомати

Дана концепція автоматів є дуже важливою у цій галузі, оскільки в ній розглядається математична модель автоматів, а також досліджують їх моделі без реалізації.

Для опису автомата використовується поняття послідовності. Послідовність зручно розглядати як часову розгортку, що змінюються дискретно і приймає значення t = 0,1,2,3, ....

Відліки такого часу будемо називати тактами. У кожному такті будемо задавати значення дискретних змінних X(t), Y(t) і S(t).

X(t) - змінна, значення якої представляються символами вхідного алфавіту X = {X₀, X₁, ... X_{N -1}} (вхідними символами);

Y(t)- змінна зі значеннями символів вихідного алфавіту Y={Y₀, Y₁, ...Y_M-1};

S(t) - змінна зі значеннями символів алфавіту станів автомата S = {S₀, S₁, ..., S_K-1}.

Автомат здійснює перетворення символів, потактно приймаючи вхідні символи X і формуючи вихідні - Y, а також змінюючи свої стани S.

При скінченності всіх алфавітів автомат називається скінченним, хоча він може перетворювати послідовності нескінченної довжини.

З точки зору властивостей перетворень, виконуваних автоматами різних видів, всі вони виявляються в кінцевому рахунку еквівалентними: можуть представляти тільки регулярні події.

У той же час різні види можуть більшою чи меншою мірою підходити для вирішення різних завдань аналізу та синтезу автоматів.

Функції переходів і виходів можуть задаватися різними способами. Найчастіше використовуються табличні і графові способи задавання. Приклад табличного задавання наведено на рисунку 3.

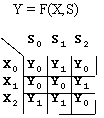
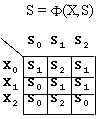
Рис. 3. Задавання функцій переходів і виходів автомата

N=3 K=3 M=3

При заданні автомата у вигляді графу, стани S ототожнюються з вершинами графа. Дуги - зваженими символами Х, задають S=Ф(X, S) (рис. 4).

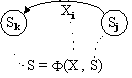
Рис. 4. Задавання функцій переходів S=Ф(X, S) у вигляді графа

Y = F(X,S) задається вагою дуги (рис. 5).

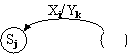
Рис. 5. Задавання функцій переходів Y = F(X,S) у вигляді графа

При Y = F(S) замість розстановки Y_j на всіх дугах, що виходять з S_k, Y_j зважують вершину S_k (рис. 6).

(*) (**)

Рис. 6. Приклад графів автоматів

Функції переходів і виходів можуть мати область визначення, меншу в порівнянні з усіма можливими наборами значень їх аргументів. При цьому ми отримуємо неповністю визначені автомати.

Знаючи функції переходів і виходів, можна описати поведінку автомата, що сприймає деяку вхідну послідовність, якщо відомо стан, в якому знаходився автомат в такт появи першого символу вхідної послідовності.

Говорячи про автомати, ми припускаємо можливість використання їх для опису або реалізації перетворень дискретної інформації.

При цьому мається на увазі наявність системи домовленостей (інтерпретації), за якою можна встановити відповідність реального часу тактам автомата.

При інтерпретації потрібно на півосі часу виділити інтервали з номерами 0,1,2, ..., що задають такти автомата (рис. 7):

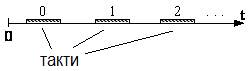
Рис. 7. Діаграма тактів автомата

Тривалість тактів (і пауз між ними) може бути будь-якою, аж до певного моменту часу. Способи розмітки часу також можуть бути різними; ми виділимо 2 з них, що визначають різні класи автоматів. З цією метою будемо розглядати автомат як об'єкт, який обмінюється вхідними і вихідними сигналами (представляють символи вхідного і вихідного алфавіту) із зовнішнім середовищем:

Такти можна виділити за допомогою деяких «таймерів» (давачів тактів), загальних як для автомата, так і для «зовнішнього середовища», наприклад, у вигляді генератора синхроімпульсів, що сигналізує про наявність такту (рис. 8).

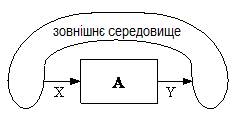
Рис. 8. Схема джерела тактів

Автомати, що працюють в такій системі тактів, називаються синхронними. Таким чином, в синхронному автоматі X і Y, такти повинні формуватися в певний час, що задається давачем тактів. Фізична модель може інтерпретуватися як синхронний автомат, наприклад, наступним чином.

Маємо генератор СІ, який виділяє на півосі часу інтервали Т (рис. 9).

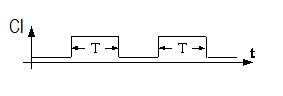
Рис. 9. Діаграма тактів автомата

Нехай під час цих інтервалів вхідні дії Х і вихідні реакції Y фізичної моделі, а також внутрішні сигнали, що представляють стани S, не змінюються (зміна X, Y і S відбувається тільки між інтервалами Т). У такому випадку інтервали Т відповідають тактовим імпульсам. Якщо поведінку фізичної моделі при цьому можна описати функціями переходів і виходів, то її можна розглядати як автомат.

Зафіксуємо часову діаграму функціонування розглянутої фізичної моделі (рис. 10):

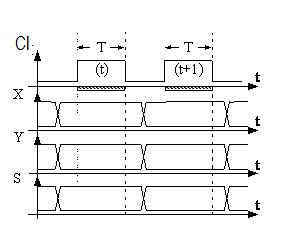
Рис. 10. Діаграма функціонування фізичної моделі

Для синхронних автоматів найбільш природні і найбільш вживані задавання вигляду:

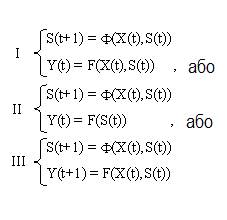
I - як правило називають автоматом Мілі,

II - автоматом Мура;

III - будемо називати автоматом Мілі із затримкою.

Можна шукати інтерпретацію, при якій деякий фізичний пристрій може розглядатися (описуватися) як автомат. Це задача аналізу.

Можна будувати фізичну модель, яку при певній інтерпретації можна вважати автоматом з необхідним законом функціонування. Це задача синтезу.

Виділяти такти за допомогою генератора синхроімпульсів (СІ) можна по різному (для різних фізичних моделей краще підходять різні інтерпретації) (рис. 11):

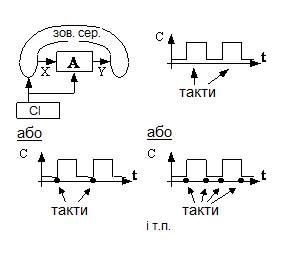
Рис. 11. Діаграми тактів фізичних моделей ЦА

В асинхронних автоматах початок і закінчення тактів визначається за фактом зміни Х на вході автомата.

Паузи між тактами представлені моментами змін Х (рис. 12).

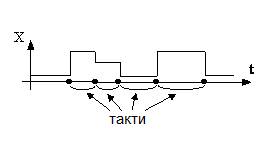
Рис. 12. Представлення пауз між тактами на часовій діаграмі тактів

Таким чином, для асинхронних автоматів такт формується зовнішнім середовищем (X і Y в асинхронному автоматі можуть формуватися в довільний період часу).

Зміна X(t) для асинхронних автоматів говорить про початок наступного такту (t+1). Нове значення X(t+1) розглядається як причина зміни стану S(t) і появи нового S(t+1). S(t+1) появляється як реакція на X(t+1) відразу ж: S(t+1) = F(X(t+1), S(t)).

Функції переходів такого виду становлять найбільший інтерес через труднощі фізичного моделювання асинхронних автоматів з

S(t+1) =F(X(t), S(t)).

Функції виходів зазвичай мають вигляд:

Y(t) = F( X(t), S(t)) , або

Y(t) = F(S(t)).

В результаті отримуємо:

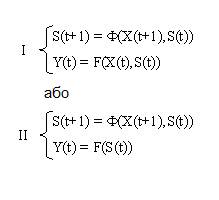
В синхронних і в асинхронних автоматах найчастіше ми маємо справу з ініціалізованими автоматами, тобто з такими, для яких задані початкові стани S(0).

Структурні автомати

Моделлю абстрактного автомата є об'єкт з 1 входом і 1 виходом (рис. 13).

Рис. 13. Модель абстрактного автомата

Ні вид сигналів, ні внутрішня структура абстрактного автомата не розглядаються. У структурній теорії автоматів об'єктом вивчення є так звані структурні автомати та їх композиції.

Структурний автомат - це об'єкт, що має сукупність вхідних і вихідних каналів (входів і виходів), по яких передаються елементарні сигнали, що представляють перероблювані автоматом символи.

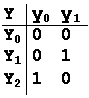
Рис. 1.14. Схема структурного автомата і його представлення у вигляді таблиці і графа

Елементарні сигнали відображають структурний алфавіт автомата. В даний час це найчастіше двійковий алфавіт (рис. 15).

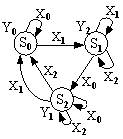
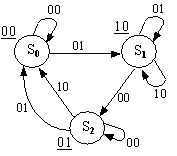
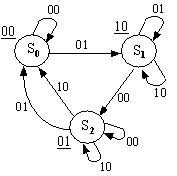
Рис. 1.15. Приклади двійкового представлення графів автомата

У прикладі структурний алфавіт для всіх символів двійковий:

x₀ = (0;1), x₁ = (0;1)

y₀ = (0;1), y₁ = (0;1)

Композиція структурних автоматів полягає в тому, що для сукупності автоматів проводиться ототожнення (з'єднання) входів і виходів окремих автоматів. Деякі входи і виходи при цьому відзначаються як зовнішні.

Автомати, що утворюють композицію, працюють в деякій системі тактів. Виділення тактів і пауз між ними на півосі часу означає розбиття часу на періоди. Період такту - час від початку i-го до початку (i +1)-го такту (i-ий період) (рис. 1.16).

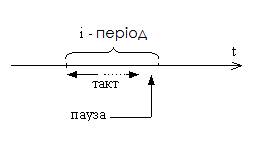
Рис. 1.16. Поділ такту на періоди

У структурній теорії автоматів поняття такту деталізується, тому що в ній, зокрема, розглядається задача побудови фізичних моделей автоматів і способи інтерпретації тактових систем.

Для автомата існує інтервал часу в періоді t, коли значення X незмінні і відповідно з функціями виходів і переходів визначають значення Y і S. Цей час будемо називати вхідним мікротактом t¹.

Інтервал часу в періоді t, коли значення Y незмінні і відповідають значенням функції виходів, будемо називати вихідним мікротактом t⁰.

У композиції автоматів з'єднання виходу автомата A_i зі входом автомата A_j можливо тільки у випадку, якщо t⁰_i сумісний з t¹_j, тобто, якщо будь-який момент часу t¹_j належить t⁰_i.

Найбільш вживані наступні варіанти організації тактів:

1. Композиції автоматів з єдиною (загальною для всіх автоматів) системою тактів.

Для такої композиції існує єдине (загальне) розбиття півосі часу на періоди тактів для всіх автоматів композиції.

2. Композиції автоматів з різними системами тактів.

У таких композиціях автомати можуть бути розбиті на підмножини автоматів, в кожному з яких використовується своя єдина система тактів.

При цьому можна виділити два основних види композицій:

а) композиції з неспряженими системами тактів;

б) композиції зі спряженими системами тактів;

У а) автомати різних підмножин не можуть обмінюватися сигналами в жодному такті через несумісність їх вхідних і вихідних мікротактів.

У б) існують такти, в яких вхідні та вихідні мікротакти автоматів різних підмножин сумісні, що дозволяє передавати між ними сигнали (рис. 1.17).

Рис. 1.17. діаграма композицій тактів

Можна виділяти спряжені мікротакти.

3. Композиції узгоджених автоматів. Узгодженим називається автомат, вхідний мікротакт якого визначається сигналами ззовні, а вихідний мікротакт - сигналами самого автомата.

У композиції

сигнали, що визначають вихідний мікротакт А_i, одночасно визначають вхідний мікротакт А_j.

Такі композиції можуть будується з автоматів з різною інерційністю (швидкістю) роботи.

В асинхронних узгоджених автоматах, названих аперіодичними, тривалість періоду кожного такту буде визначатися швидкісними властивостями конкретних автоматів композиції. (Зовнішнє середовище при цьому розглядається як автомат композиції.)

Найчастіше ми розглядаємо композиції синхронних автоматів з єдиною системою тактів, або композиції синхронних автоматів зі сполученими системами тактів.

Композиція - автомат, якщо:

для кожного автомата А_i композиції в будь-якому його вхідному мікротакті (і вихідному) на будь-якому його вході (і виході) присутній сигнал, однозначно встановлюється деякий символ з його алфавіту. Під даною умовою слід розуміти наступне:

1. необхідність ототожнення всіх елементарних входів і виходів;

2. неприпустимість ототожнення входу і виходу при розбіжності вхідних мікротактів з відповідними вихідними;

3. неприпустимість ототожнення двох і більше виходів;

4. неприпустимість сполук, що дають в композиції «стійкі петлі»

Кодування станів автомата

Вирішуючи задачу кодування станів, ми будемо вважати, що кодування вхідного і вихідного алфавітів задано, хоча в принципі це не обов'язково, так як подібна ситуація найчастіше зустрічається на практиці.

Різні варіанти кодування станів автомата дозволяють отримувати схеми, різниця між якими полягає в наступному:

1. складності комбінаційної схеми (КС), що реалізують функції збудження і виходів;

2. можливості збереження працездатності схеми при відмовах окремих її елементів (відмовостійкості);

3. надійності роботи в умовах можливих неузгодженостей тактів елементарних автоматах (ЕА).

Вибір ЕА.

Складність КС автомата залежить від того, які типи ЕА використовуються в автоматі, так як для різних ЕА потрібні різні функції збудження. Оптимальний вибір ЕА пов'язаний з перебором великого числа варіантів схем. Завдання ускладнюється тим, що в загальному випадку вибір ЕА слід поєднувати з вибором кодів станів.

Наближене рішення задачі вибору ЕА можна проводити на основі локального незалежного підбору типів окремих ЕА з числа перебраних.

Переглянувши ЕА_i для i = 0 … k -1, виберемо набір ЕА.

Розглядаючи ЕА_i потрібно для кожного типу ЕА_i: D, T, JK, і т.д. отримати функції збудження і вибрати тип ЕА, що вимагає найбільш просту КС. Оцінка складності КС може виходити по різному в залежності від використовуваних ЛЕ. Можна будувати прототип КС, використовуючи прості прийоми синтезу; можна оцінювати за кількістю кон'юнкцій в ДНФ; можна оцінювати за кількістю змінних і т.п.

Слід зазначити, що на практиці вибір з l типів ЕА часто пов'язаний з доцільністю використання одного типу всіх k ЕА. При цьому перебір скоротиться з k - l до l варіантів. У деяких випадках вибір типів ЕА обумовлюється міркуваннями, не пов'язаними зі складністю КС автомата, наприклад, з порівняльними характеристиками окремих типів ЕА: надійність, споживана потужність і т.д.

В синтаксисі мови Verilog передбачені наступні оператори, виконання яких здійснюється паралельно:

• assign;

• always;

Таким чином, якщо в програмі для опису модуля використовується декілька операторів assign і always, всі вони будуть виконуватися одночасно.

Роботу логічного пристрою, описаного за допомогою мов HDL, можна перевірити двома способами: або на персональному комп'ютері (моделювання), або безпосередньою реалізацією в мікросхемі. Процес синтезу набагато складніший за моделювання, оскільки передбачає, крім компіляції коду, ще й синтез логічної схеми (тобто реалізацію пристрою за допомогою доступних компонентів ПЛІС і трасування провідників в обраній мікросхемі). Тому результат застосування деяких конструкцій мови Verilog при моделюванні та синтезі відрізняється! Не всі оператори мови Verilog є синтезуючими!

Оператор assign використовується для безперервного присвоєння сигналу змінної типу wire і має наступний синтаксис:

assign var = expression;

Дія оператора трактується так: при зміні виразу expression (наприклад, змінилося значення змінної, що входить до expression) обчислюється нове значення виразу і результат присвоюється змінній var. У лівій частині виразу змінна може бути тільки типу wire, а в правій частині - можлива комбінація змінних wire, reg, integer. Всі оператори assign в модулі виконуються паралельно.

Оператор always - це один з основних, ефективних операторів мови Verilog. Він дозволяє задати постійне виконання послідовності команд. Зазначена послідовність може виконуватися або циклічно (у нескінченному циклі), або тільки після появи певної події. Синтаксис цього оператора:

always @ (... events ... )

begin

...

// послідовність операторів (виконується послідовно, один за одним)

...

end

Даний оператор застосовується тоді, коли виникає необхідність послідовного виконання команд. Для цього, після ключового слова always, іде послідовність операторів, вкладених в блок begin / end. Всі команди, розташовані всередині такого блоку, виконуються послідовно, а самі оператори always - паралельно. За відсутності блока begin / end - дія оператора always поширюється тільки на один наступний за ним оператор. Якщо в операторі always відсутня конструкція @(... events ...), то послідовність команд, розташованих між begin і end, виконується в нескінченному циклі.

Для задавання умови, необхідної для запуску блоку always, використовується конструкція @(... events ...). У цьому випадку, всередині круглих дужок вказується список умов (подій), котрі спричинюватимуть виконання оператора always. Умовою може бути поява позитивного або негативного фронту, зміна значення сигналу і т. д. Позитивний фронт вказується ключовим словом posedge, негативний фронт - negedge. Після ключових слів posedge і negedge слідує назва сигналу. Якщо необхідною умовою є будь-яка зміна сигналу - в дужках просто вказується ім'я контрольованого сигналу.

Важливе зауваження! Усередині оператора always не можна використовувати змінні типу wire (тобто всі змінні, яким присвоюється значення усередині даного оператора, повинні бути типу reg). Інакше це призведе до помилок компіляції. Усередині оператора always неможливий виклик іншого модуля. Всі оператори always виконуються паралельно.

Реалізація цифрових автоматів на ПЛІС ALTERA DE-2

Для демонстрації моделей цифрових автоматів, реалізованих на ПЛІС Altera DE2, наведено два приклади автоматів Мілі та Мура. Структурна схема автомата Мілі зображена на рис. 1.18.

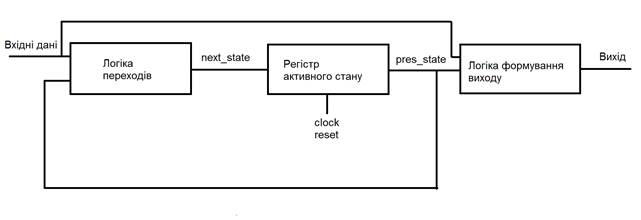
Рис. 1.18. Структурна схема автомата Мілі

Вихідний сигнал автомата Мілі, залежить від текучого стану автомата і вхідного сигналу.

Структурна схема автомата Мура зображена на рис. 1.19.

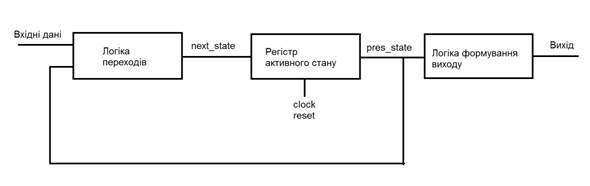
Рис. 1.19. Структурна схема автомата Мура

Вихідний сигнал автомата Мура, залежить тільки від поточного стану автомата.

Як відомо, скінченний автомат може знаходитися в кожен конкретний момент часу тільки в одному стані. Кожен тактовий імпульс викликає перехід автомата з одного стану в наступний. Правила переходів і визначаються комбінаційною схемою, названою логікою переходів. Наступний стан визначається як функція текучого стану і вхідного сигналу.

Регістр активного стану представляє собою набір тактованих D-тригерів синхронізованих одним синхросигналом і використовується для зберігання коду текучого стану автомата. Очевидно, що для автомата з n станами потрібно log2(n) тригерів.

Логіка формування виходу. Вихід ЦА зазвичай представляється як функція текучого стану і вихідної позиції (у випадку автомата Мілі). Формування вихідних сигналів автомата визначається за допомогою логіки формування виходу.

Для зручності, сполучення частин логіка переходів і регістр активного стану, я зробив однаковими для обох автоматів. Діаграма переходів для автоматів Мілі та Мура зображена на рис. 1.20.

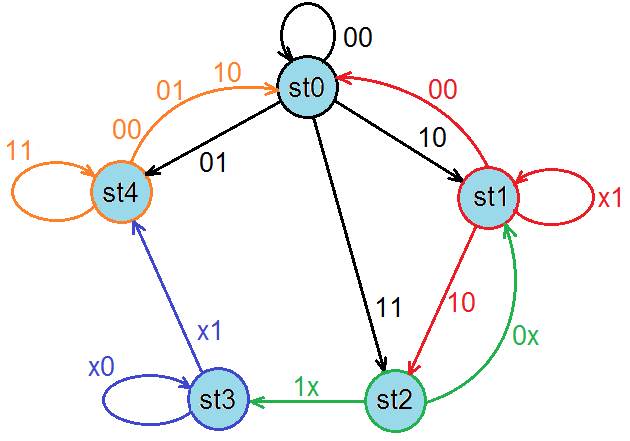
Рис. 1.20. Діаграма переходів. st0 - st4 – стани в яких може знаходитись автомат; 00 , 01, 10, 11, x1, 0x, 1x, x0, x1 – двобітні вхідні сигнали;

х – невизначене значення біта (0, або 1)

Цей граф показує. що досліджувані автомати Мілі та Мура можуть перебувати в 5-х станах, причому поточний стан перебування автомата залежить від попереднього стану автомата і вхідного сигналу попереднього такту. ЦА переходить з одного стану в наступний при кожному такті. Переходи між станами, зображені на графі, можуть бути довільними, або такими що відповідають конкретній задачі закладеній в автомат, так само і кількість станів автомата.

Апаратні засоби ПЛІС дозволяють дуже просто реалізувати будь-які логічні структури в тому числі ЦА. Для цього потрібно написати код відповідних програм і підключити входи і виходи цих програмних модулів до відповідних контактів стенду DE2. З графа бачимо, що вхідний сигнал складається з двох бітів, для цього доцільно задіяти два перемикачі, наприклад SW[0] і SW[1]. Вихідний сигнал складається лише з одного біту, для його реєстрації доцільно задіяти один з світлодіодів, наприклад LEDR[17]. Щоб процес відбувався динамічно, використовується вбудований генератор тактових сигналів CLOCK_50, з частотою 50 МГц, але пряме його використання не дасть хорошого візуального ефекту оскільки процес відбуватиметься дуже швидко і буде неможливо спостерігати за послідовністю роботи автоматів, для цього ця частота понижується за допомогою подільника частоти до 2 Гц. Для відображення поточного і наступного станів автомата використовуються два 7-сегментні індикатори HEX7 і HEX0 відповідно, на які виводиться цифра стану. Для забезпечення стабільної і безвідмовної роботи використовується скидання автомата в початковий стан, для цього було підключено кнопку KEY[0]. Таким чином завжди забезпечується ініціалізація автомата в наперед передбаченому стані при першому тактовому імпульсі. У випадку, якщо скидання не передбачається, неможливо спрогнозувати, з якого початкового стану почне функціонувати автомат, що може призвести до збоїв в роботі всієї системи. Особливо ця ситуація актуальна при включення живлення системи. Зазвичай застосовуються асинхронні схеми скидання, через те, що не потрібно використовувати дешифратор невикористовуваних (надлишкових) станів, що спрощує логіку переходів.

Блок-схема алгоритму формування вихідного сигналу для автомата Мура зображено на рис. 1.21.

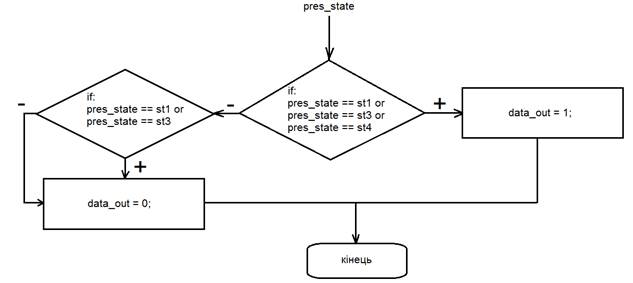
Рис. 1.21. Блок-сема алгоритму блока «логіка формування виходу» автомата Мура. pres_state – регістр для зберігання активного стану автомата;

data_out – вихідні дані

Блок-схема алгоритму формування вихідного сигналу для автомата Мілі зображено на рис. 1.22.

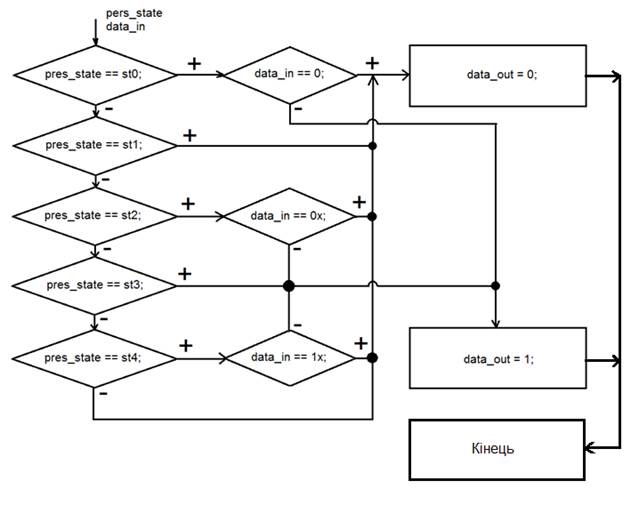
Рис. 1.22. Блок-сема алгоритму блока «логіка формування виходу» автомата Мілі. pres_state – регістр для зберігання активного стану автомата;

data_in – вхідні дані; data_out – вихідні дані

Оскільки ПЛІС, виконані по архітектурі FPGA мають достатню кількість регістрів (тригерів), використання автоматних моделей дозволяє отримати достатньо швидкодіючу і, в той же час, наочну реалізацію при помірних затратах ресурсів. Мова опису пристроїв Verilog HDL, на якій були реалізовані дані автомати, має достатній набір операторів для реалізації різноманітних програм на ПЛІС. На рис.1.23 наведено приклади роботи програми:

Рис. 1.23. Приклад роботи комбінаційної схеми автоматів Мілі та Мура.
Зліва зображена цифра текучого стану автомата, справа – наступного