И его графическое изображение
Схема полусумматора формирует перенос в следующий разряд, но не учитывает перенос из предыдущего разряда, поэтому она и называется полусумматором. Заполним таблицу истинности полного двоичного одноразрядного сумматора, учитывающего входной перенос.
На таких сумматорах возможно построение многоразрядных сумматоров, выполняющих арифметическое сложение двух чисел в двоичном коде.
Построим таблицу истинности для сумматора (табл. 2.14.3), где PI – входной перенос, PO – выходной перенос, формируемый схемой.
Таблица истинности полного двоичного одноразрядного сумматора.
Таблица 2.14.3
| PI | a | b | S | PO |
Пользуясь таблицей истинности, запишем логические выражения для выходных величин S и PO в СДНФ.
S = PI* a* b v PI* a b* v PI a* b* v PI a b
PO = PI* a b v PI a* bv PI a b*v PI a b
Уравнение для суммы не минимизируется. Уравнение для переноса можно преобразовать к виду:
PO = a b v PI b v PI a
Схема полного сумматора приведена на рисунке 2.14.4. В этой схеме не учтено преобразование функции переноса.
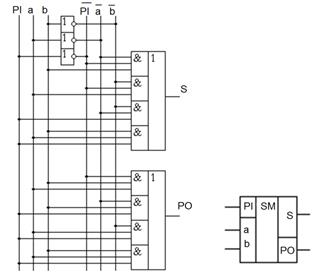
Рис. 2.14.4 Схема двоичного одноразрядного сумматора
И его графическое изображение
Для того чтобы получить многоразрядный сумматор, достаточно соединить выходы переносов младших разрядов с входами переносов соответствующих старших разрядов одноразрядных сумматоров. На схеме PI –входной перенос 4-х разрядного сумматора, PO – выходной перенос, S0, S1, S2, S3 – соответствующие разряды полученной при сложении суммы.
Схема соединения одноразрядных сумматоров для реализации четырехразрядного сумматора приведена на рисунке 2.14.5.
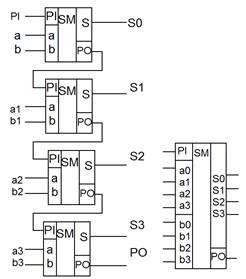
Рис. 2.14.5. Схема четырехразрядного двоичного сумматора и его графическое изображение.
В приведенном на рисунке 4-х разрядном сумматоре процесс передачи переносов в старшие разряды имеет последовательный характер. Сигнал переноса в каждом разряде формируется после того, как будет сформирован и передан сигнал переноса из предыдущего разряда. Самым длительным процессом распространения переноса будет случай, когда в каждом разряде последовательно будет сформирован перенос. Если обозначить t – задержку формирования перенса в одном разряде, то самый длительный процесс формирования переноса в n-разрядном сумматоре T = nt.
В реальных схемах для увеличения скорости работы двоичного сумматора применяется дополнительная схема формирования переносов для каждого двоичного разряда.
Принцип ускоренного переноса заключается в том, что для каждого двоичного разряда дополнительно находятся два сигнала:
G — образование переноса и H — распространение переноса.
GI = ai·bi
HI = ai + bi
Если ai=bi=1, то Gi=1 и в i-разряде формируется сигнал переноса Pi+1 в следующий высший разряд независимо от формирования функций суммы в предыдущих разрядах.
Если хотя бы одно из слагаемых ai или bi равно «1», то HI=1и перенос в последующий разряд производится при наличии сигнала переноса из предыдущего разряда.
Если Hi=Hi–1=1 и при этом существует сигнал переноса Pi из предыдущего в i-й разряд, то перенос производится сразу в i+2 разряд.
Процесс формирования ускоренного переноса описывается следующим уравнением:
PI+1 = GI + HI·GI–1 + HI·HI–1·GI–2 + … + HI·HI–1·…·H2·H1·P1
Блоки ускоренного переноса выпускаются в интегральном исполнении в виде отдельных микросхем или встраиваются в микросхемы сумматоров и арифметико-логических устройств.
