Силы, действующие на движущуюся массу воздуха

Сила барического градиента. С появлением барического гради­ента возникает горизонтальное движение воздуха, так как бари­ческий градиент является силой, приложенной к единице объема.

Однако для многих расчетов удобнее рассматривать движу­щую силу барического градиента, приложенную не к единице объема, а к единице массы воздуха. Для этого объем (см³) следу­ет умножить на плотность (г/см³). Тогда

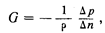
где G — движущая сила барического градиента, имеющая раз­мерность ускорения:

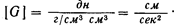
Казалось бы, что если движущая сила выражается ускорением, то вызываемое ею движение должно быть равноускоренным, т. е.

скорость должна непрерывно возрастать. Однако итого не проис­ходит, потому что как только масса воздуха приходит в движе­ние, 'на нее начинают действовать отклоняющие и тормозящие силы: отклоняющая сила вращения Земли, сила трения и центро­бежная сила.

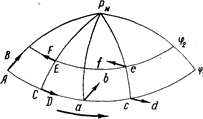Рис 20. Отклоняющее действие вра­щения Земли на движущуюся массу

Сила Кориолиса. Отклоняющая сила вращения Земли, или сила Кориолиса, — результат того, что мы определяем направ­ление движения по отношению к вращающимся земным координа­там, а движущаяся масса по инерции стремится сохранить прямолинейное движение по от­ношению к неподвижным коорди­натам, например по отношению к неподвижным звездам. Иначе говоря, движущаяся масса (воз­духа, воды и всякого другого те­ла) сохраняет движение в на­правлении того светила, на кото­рое оно было первоначально направлено, и следует за ним при его видимом движении по небесному своду, т. е. в северном полуша­рии отклоняется вправо, а в южном—влево от первоначального направления.

Как видно из рис. 20 направление движения сохраняется в мировом пространстве {AB\\ab, CD\\cd, EF\\ef), во всех случаях отклоняясь вправо (северное полушарие) от направления мери-дианов и параллелей земного шара.

Величина отклоняющей силы вращения Земли определяется формулой

А == 2wsin<fv, где (в=7,29Х10~⁵ сек-¹—угловая скорость вращения Земли;

<р — широта места;

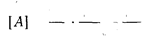v—скорость движения массы воздуха (скорость ветра).

_ l CM _•_ CM

~ сек сек ~^, сек² ' т. е. размерность та же, как и у силы барического градиента. . Подсчеты показывают, что и по величине она того же порядка, что и сила барического градиента (на широте 30°—0,07 см/сек², на полюсе—0,15 см/сек² при скорости ветра 10 м/сек, а на эквато­ре отклоняющая сила отсутствует, так как sinq>==0).

Как видно из формулы, отклоняющая сила Кориолиса прямо пропорциональна широте места (увеличивается от экватора к полюсам) и скорости ветра (чем больше скорость, тем больше отклоняющая сила).

Сила Кориолиса в каждый данный момент направлена перпен­дикулярно к направлению движущейся массы (вправо в север­ном полушарии, влево—в южном).

Сила трения. Сила трения в основном сказывается в нижних

слоях атмосферы и вызывается тем, что воздушная масса переме­щается над шероховатой подстилающей поверхностью, вследствие чего воздушные частицы, непосредственно соприкасающиеся с земной (или водной) поверхностью замедляют движение. В ре­зультате перемешивания частицы с уменьшенной скоростью пе­реносятся вверх, 'на место их сверху поступают частицы с большой скоростью, скорость которых при со­прикосновении с земной поверхностью также замедляется и т. д.

Рис. 21. Равномерное прямоли­нейное движение воздуха при наличии силы трения

В результате в некотором слое, на­зываемом слоем трения, скорость воз­душного потока уменьшается, боль­ше—у самой земной поверхности, меньше—по мере увеличения высоты. Высота, на которой сила трения прак­тически исчезает, называется уровнем трения. В зависимости от степени пере­мешивания и от степени шерохова­тости (неровности) земной поверхно­сти уровень трения бывает на высоте от 500 до 1500 л<, а в среднем прини­мается равным 1000 м (в горных рай­онах больше).

Сила трения у земной поверхности

/? = - kV,

где k — коэффициент трения, зависящий от степени шероховато­сти подстилающей поверхности; на суше он может дости­гать 12Х10-⁵ се/с-¹, над океанами 2><10~⁵ се/с-¹;

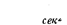v — скорость ветра.

Размерность силы трения [Щ == -'—. Знак минус указывает,

что сила трения направлена в противоположную сторону от на­правления ветра v, т. е. она уменьшает скорость движения массы воздуха (скорость ветра). •«

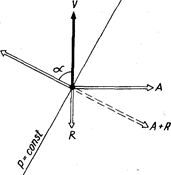
Отклонение ветра от изобар. Чтобы возникшее под действием силы барического градиента движение воздуха стало равномерным и прямолинейным, силу барического градиента необходимо урав­новесить векторной суммой отклоняющей силы вращения Земли и силы трения (рис. 21), т. е. чтобы G==A-\-R, где G—сила бари­ческого градиента, А — сила Кориолиса, R — сила трения. Из ри­сунка видно, что при наличии силы трения R направление призем­ного ветра v отклоняется от направления барического градиента G на угол (х-<90°, т. е. пересекает изобару в сторону более низкого давления.

Величину этого отклонения (угол ос) нетрудно рассчитать, если

учесть, что согласно рис. 21д-= sinoi- == cosx. Таким обра­зом были вычислены углы отклонения направления ветра вблизи

Таблица 4

у, г/здй	О
а	о
.?

поверхности океана от направления градиента ос или изобары р на различных широтах (р (табл. 4).

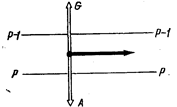Рис. 22. Геострофическии ветер

Над сушей коэффициент трения k менее определен из-за разно­образия в рельефе и существенного влияния распределения темпе­ратуры воздуха по высоте. Так, над ровной местностью k меньше, „ над пересеченной — больше. Влияние распределения температуры состоит в том, что при инверсиях, т. е. при по­вышении температуры воздуха с высо­той, воздухообмен с более высокими слоями затруднен или полностью ис­ключается. А такое положение над сушей в ночные часы наблюдается ча­сто. Поэтому в умеренных широтах над равнинной местностью угол отклоне­ния ветра от градиента а в среднем

составляет около 60°, а ночью при инверсиях уменьшается до 45—50°, над морем соответственно 80—85° и 60—65°.

Геострофический ветер. При отсутствии силы трения сила ба­рического градиента на прямолинейных изобарах уравновешива­ется одной отклоняющей силой вращения Земли А, которая в этом случае будет направлена прямо противоположно G, а ветер при­мет направление по изобаре (сс=90°), оставляя низкое давление слева в северном полушарии и справа — в южном.

Такой ветер, наблюдающийся при прямолинейных изобарах выше уровня трения, называется геострофическим (рис. 22, жир­ная стрелка). Его скорость

4,8 \р , . , ^⁼^^\^мice^•

Здесь — должно быть в мб/град • мер.

Центробежная сила. Градиентный ветер. Изобары не всегда прямолинейны, а при криволинейном движении воздуха появляет­ся центробежная сила. Ее величина

С=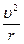

где r— радиус кривизны траектории (изобары).

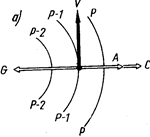
Центробежная сила направлена по радиусу кривизны траектории. В циклоне она направлена против силы градиента и совпадает с отклоняющей силой вращения Земли, в антициклоне совпадает с силой барического градиента (рис. 23). Отсюда можно сделать вывод, что при одном и том же градиенте скорость ветра в циклоне меньше, а в антициклоне больше, чем при прямолинейных изо­барах.

Движение воздуха под действием сил градиента, центробежной и Кориолиса и при отсутствии трения называется градиентным ветром.

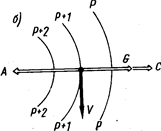Рис. 23. Градиентный ветер: а—в циклоне, б—в антициклоне

расстояние между изобарами (при изобарах через 5 мб) в градусах меридиан. Рис. 24. Градиентная линейка

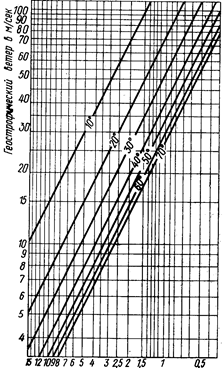Градиентная линейка. Расчет скорости ветра над морем может быть выполнен по формуле. Вместе с тем предложен ряд номограмм, именуемых гради­ентными линейками, с помо­щью которых по расстоянию между изобарами определяет­ся скорость геострофического ветра, а по направлению изо­бар — его направление.

Большинство градиентных линеек рассчитано для карт определенного масштаба. Од­нако линейка, рекомендуемая Государственным океаногра­фическим институтом (ГОИН), пригодна для карт любого масшта-ба (рис. 24). Она рас­считана по приведенной выше формуле геострофического вет­ра.

Пользование линейкой весь­ма просто. Циркулем снимают расстояние между изобарами (по нормали к ним) и измеря­ют в градусах меридиана.

Полученное значение нахо­дят на нижней шкале линей­ки, от него поднимаются вер­тикально вверх до наклонной линии, соответствующей широ­те места, для которого определяется ветер. Промежуточные значения широты находят интерпо­ляцией. Далее, по горизонтали смещаясь влево, на вертикальной шкале отсчитывают скорость геострофического ветра.

Полученная скорость геострофического ветра еще не будет скоростью ветра вблизи поверхности моря. Для перехода к послед­ней необходимо скорость геострофического ветра умножить на коэффициент, зависящий от разности температур воды и воздуха (табл. 5).

Таблиц а 5

Разность температур	Коэффициент
Вода холоднее воздуха Вода теплее воздуха	f более чем на 0,5° l на 0,5—0,1° Г на 0,0—2,0° [ более чем на 2,0°	0,5 0.6 0,7 0,8

Если разность температур не измерялась, то берется коэффи­циент 0,7.