Измерительных сигналов. К элементарным измерительным сигналам относятся постоянный во времени сигнал и сигналы, описываемые единичной и синусоидальной функциями
К элементарным измерительным сигналам относятся постоянный во времени сигнал и сигналы, описываемые единичной и синусоидальной функциями, а также дельта-функцией.
Постоянный сигнал — самый простой из элементарных сигналов, описываемый математической моделью вида Y = А, где А — единственный параметр сигнала. Графики временной и частотной моделей постоянного сигнала приведены на рис. 10.4.
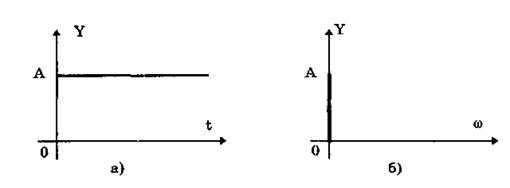
Рис. 10.4. Графики временной (а) и частотной (б) моделей
постоянного сигнала
Единичная функция, называемая иногда функцией Хевисайда, описывается уравнением
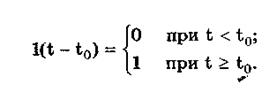
Она имеет один параметр — момент времени t0. Ее временная и частотная модели представлены на рис. 10.5,а.
Дельта-функция описывается уравнением
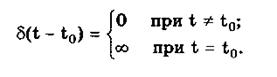
Она также имеет один параметр — момент времени t0. Графики временной и частотной моделей дельта-функции d(t) показаны на рис. 10.5, б. Из них видно, что дельта-функция имеет спектр бесконечной ширины.
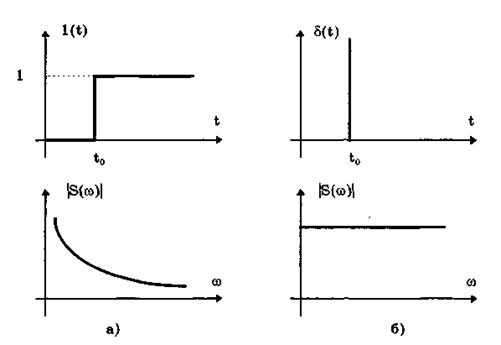
Рис. 10.5. График моделей единичной (а) и дельта-функции(б)
Дельта-функция обладает следующим свойством:
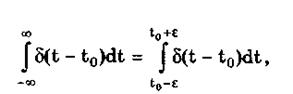
где e — любое, сколь угодно малое число. Она может рассматриваться как предельная функция однопараметрического семейства непрерывных функций, например нормального распределения с бесконечно малым СКО s:
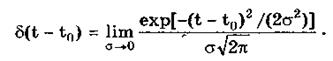
Единичная и дельта-функции связаны между собой следующими выражениями:
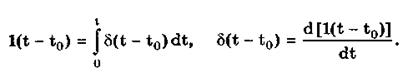
Важной особенностью дельта-функции является стробирующее действие, которое описывается уравнением
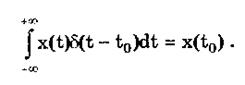
Оно используется для представления дискретизированной во времени функции с шагом дискретизации Dt:
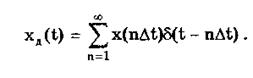
Гармонический сигнал описывается уравнением
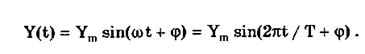(10.5)
Параметрами такого сигнала являются: амплитуда Ym, период Т (или частота f=l/T, или круговая частота w) и начальная фаза j. График временной модели общеизвестен, а график частотной модели такого сигнала показан на рис. 10.6
. 
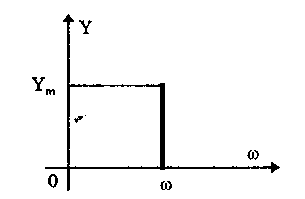
Рис. 10.6. Спектр гармонического сигнала