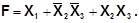Минимизация не полностью определенных

Булевых функций

В устройствах автоматики дискретного действия могут применяться такие схемы, для которых некоторые комбинации сигналов на входы никогда не подаются. Такие комбинации называются запрещенными или нейтральными. При проектировании такого устройства на запрещенных наборах можно выбирать значение функции произвольно (т.к. в реальной схеме эти наборы быть не могут). Выбрать значения функции на запрещенных наборах нужно таким образом, чтобы функция была наиболее простой.

Рассмотрим метод получения минимальной ДНФ не полностью определенной булевой функции. Пусть булева функция F(X₁,X₂,...,A_n) не определена на P наборах

аргументов. Будем называть полностью определенную функцию j эквивалентной функции F, если ее значения совпадают со значениями функции F на тех наборах, в которых функция F определена. Введем две эквивалентные функции j₀ и j₁. Пусть j₀ равна нулю на всех запрещенных наборах, j₁ равна на этих наборах единице. Минимизация функции Fпо методу Квайна сводится к следующему. Для функции j₁ нужно выполнить все операции склеивания и поглощения и найти все простые импликанты. Затем составить импликантную матрицу, в которой должны быть конституенты единицы, взятые из функции j₀ (они те же, что и в исходной не полностью определенной функции F), и простые импликанты, полученные по функции j₁. Из импликантной матрицы нужно выбрать минимальное число импликант, которые накрывают все конституенты единицы.

Пример. Пусть не полностью определенная функция трех аргументов задана таблицей истинности (табл.6). Эквивалентная ей функция φ₁ имеет вид:

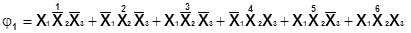
Проводим операции неполного склеивания и поглощения:

1 - 3 – 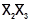3 - 5 –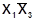

2 - 6 – 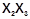4 - 6 –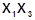

3 - 4 – 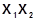5 - 6 –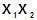

В результате получим:

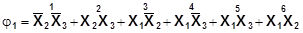
Снова проводим операции неполного склеивания и поглощения:

3 - 6 - X₁

4 - 5 - X₁

Результат этого этапа:

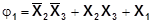
Больше ничего не склеивается, значит полученное выражение представляет собой дизъюнкцию всех простых импликант заданной функции. Для выяснения, нет ли в полученном выражении “лишних” импликант, строим импликантную матрицу, в которую заносим конституенты единицы по эквивалентной функции j₀ (см. Табл. 7). Из матрицы следует: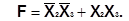

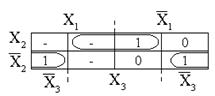Рис. 26. Карта Карно для не полностью определенной булевой функции

Решение подобной задачи с помощью карты Карно рассмотрим на примере той же функции, заданной табл. 6. Карта Карно для этой функции показана на рис. 26. На карту нанесены единицы и нули для обязательных наборов и проставлены прочерки на нейтральных наборах. Заполняем нейтральные наборы либо единицами, либо нулями таким образом, чтобы заданные единицы совместно с добавленными накрывались наибольшим

по площади правильным прямоугольником. В результате покрытия получим: