Дифференциальные операторы

Простейшей моделью края на изображении является прямая, разделяющая две контрастные области (рис. 1). Нам понадобится единичная ступенчатая функция и (z), определяемая в виде

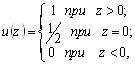
имея в виду, что она является интегралом от одномерного единичного импульса:

.

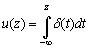Предположим, что край располагается вдоль прямой 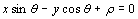. Тогда яркость изображения можно записать в виде

.

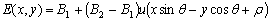Частные производные описываются уравнениями:

,

.

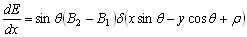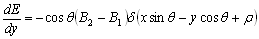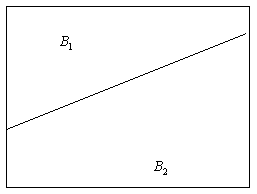
Рис. 1. Идеальный край в виде прямой, разделяющей две области постоянной яркости.

Эти дифференциальные операторы являются направленными, поскольку результат их действия зависит от ориентации края. Вектор ( 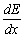, 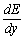) называется градиентом яркости. Градиент яркости представляет собой вектор, не зависящий от выбора системы координат, в том смысле, что он сохраняет свою величину и ориентацию по отношению к лежащему в основе образу, когда этот образ поворачивается или сдвигается.