Определение 3. Импликацией двух высказываний А и В называется высказывание, обозначаемое А Þ В, ложное лишь в том случае, когда А - истинно, а В – ложно

Элементы математической логики. 8.

Высказывания и логические операции над ними.

Термин логика происходит от греческого слова логос, которое означает мысль, разум, слово, понятие. Логика является наукой о законах и формах правильного мышления. Она изучает формы рассуждений, отвлекаясь от их конкретного содержания.

Под высказыванием будем понимать любое предложение, про которое можно сказатьистиннооноилиложно.Например, « 5+4=9 »или«человек происходит от приматов» - высказывания, первое из них - истинно, второе – неизвестно является истинным или нет, но одно из этих значений обязательно имеет. А вот «Слава великому Ленину!» или «Когда родился Сталин?» - высказываниями не являются. Математическую логику (МЛ) интересует лишь истинно или ложно то или иное высказывание и ничего более.

Для обозначения конкретных (фиксированных) высказываний будем использовать первые (прописные) буквы латинского алфавита: А,В,С,…, а для обозначения переменных высказываний – последние: X,Y,Z,… . В МЛ есть операции, посредством которых строятся новые высказывания из уже имеющихся, введём их.

Определение 1. Конъюнкцией двух высказываний А и В называется высказывание, обозначаемое А 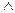Определение 3. Импликацией двух высказываний А и В называется высказывание, обозначаемое А Þ В, ложное лишь в том случае, когда А - истинно, а В – ложно - student2.ru В (или А&В), истинное лишь в том случае, когда истинны оба высказывания А и В одновременно и ложное в любом другом случае. Определение 3. Импликацией двух высказываний А и В называется высказывание, обозначаемое А Þ В, ложное лишь в том случае, когда А - истинно, а В – ложно - student2.ru

Примеры. 1). Высказывание А: Гоша приобрёл компьютер; высказывание В: Гоша чрезмерно увлёкся компьютерными играми. Высказывание А&B: Гоша приобрёл компьютер и чрезмерно увлёкся компьютерными играми.

2) А: 4 > 5; В: 5 – число простое. А&B: (4 > 5)&(5 – число простое) – ложное высказывание, ибо высказывание А в данном случае ложно. Полезно отметить, что в МЛ (в отличие от живых языков: русского, английского и т. д.) принято связывать логическими операциями любые (возможно даже не связанные друг с другом по смыслу) высказывания.

3) А: 4 – составное число; В: 6 делится на 2. А&В: (4 – составное число) и (6 делится на 2) – истинное высказывание.

Определение 2. Дизъюнкцией двух высказываний А и В называется высказывание, обозначаемое А В, ложное лишь в том случае, когда ложны одновременно оба высказывания А и В и истинное в противном случае.

Примеры. 1). А: 5< 8; В: 5=2. АÚВ: (5<8) или (5=2) – истинное высказывание.

2). (1 – простое число): А; (5>3): В. АÚВ: (1 – простое число) или (5>3) – истинное высказывание.

3). А: 7 делится на 2; В: Ö4 = -2. АÚВ: (7 делится на 2) или (Ö4=-2) – ложное высказывание.

Определение 3. Импликацией двух высказываний А и В называется высказывание, обозначаемое А Þ В, ложное лишь в том случае, когда А - истинно, а В – ложно.

А Þ В – читается так: «из А следует В», или «А влечёт за собой В», или «если А то В».

В последующем мы будем использовать лишь математические высказывания.

Примеры. 1). А: 8 > 3; В: 8 делится на 3. АÞВ: [если(8>3), то (8 делится на 3) – ложное высказывание].

2). А: sin45°=1; В: Ö2 – рациональное число. АÞВ: [если (sin45°=1), то Ö2 – рациональное число] – истинное высказывание.

3). А: 6 делится на 2; В: 6 – чётное число. АÞВ: (если 6 делится на 2, то 6 – число чётное) – истинное высказывание.

Определение 4. Эквиваленцией двух высказываний А и В называется высказывание, обозначаемое АÛВ, истинное когда оба высказывания А и В принимают одинаковые значения и ложное – в противном случае.

А Û В – читается так: «А равносильно В», или «А тогда и только тогда, когда В», или «

Примеры. 1). А: 4 делится на 2; В: 4 – число чётное. АÛВ:4 делится на 2 тогда и только тогда, когда 4 – число чётное – истинное утверждение.

2). А: 3ÎR; В: 3 делится на 2. АÛВ: ( 3ÎR тогда и только тогда, когда 3 делится на 2) – ложное высказывание.

Определения 1 – 4 можно записать в виде так называемых таблиц истинности

А	В	А&B	АÚВ	. АÞВ	АÛВ
И И Л Л	И Л И Л	И Л Л Л	И И И Л	И Л И И	И Л Л И

Ниже запись АºИ будет означать: высказывание А имеет истинное значение; а - АºЛ: высказывание А имеет ложное значение.

Определение 3. Импликацией двух высказываний А и В называется высказывание, обозначаемое А Þ В, ложное лишь в том случае, когда А - истинно, а В – ложно - student2.ru Определение 5. Отрицанием высказывания А называется высказывание, обозначаемое ØА (или А ), истинное лишь тогда, когда А – ложно.