Число единиц наблюдений по группам

(в абсолютных и относительных единицах)

Номер группы	Нижняя и верхняя границы признака 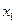, руб	Число единиц наблюдения
Абсолютные величины	Проценты
	3240-4700		10,0
	4700-6160		16,7
	6160-7620		23,3
	7620-9080		33,3
	9080-10540		10,0
	10540-12000		6,7
Итого	-		100%

Из анализа табл.7 следует, например, что в 1-ю группу с месячным доходом 3240-4700 руб. входят 3 семьи (графа 3 таблицы 7). В базовой таблице 1 они находятся под 15, 17 и 23 номерами наблюдения. Их месячные доходы составляют, соответственно, 3240, 4200 и 4400 рублей. Указанные три семьи составляют 10% от общего числа наблюдаемых семей ( 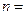30), что показано в 4 графе табл.7.

Просуммируем значения признаков 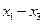по каждой из шести групп и вычислим их процентное соотношение по отношению к итоговому обобщающему показателю. Результаты расчета представлены в табл.8

Таблица 8

Групповые обобщающие итоговые показатели признаков

(в абсолютных и относительных единицах)

Номер группы	Показатели
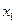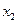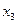руб.	процент	руб.	процент	чел.	процент
		5,29		5,92		14,29
		11,72		12,6		16,96
		21,39		21,83		25,00
		37,95		38,86		29,46
		13,16		12,51		8,93
		10,49		8,28		5,36
Итого

Из 2 графы табл.8 следует, что, например, суммарный годовой доход первой группы семей составляет: 3240 + 4200 + 4400 = 11840 руб. Это соответствует (11840/223975) 100% = 5,29 % (графа 3 табл. 8). Соответственно, суммарные расходы на питание этой же группы семей составили 6500 руб.(графа 4), что составляет 5,92% (графа 5) по отношению к итогу 109890 руб. Общее число членов семьи этой группы составляет 16 человек (графа 6). По отношению к общему числу членов семей 112 человек это соответствует 14,29 % (графа 7).

Рассчитаем простые средние арифметические величины признаков 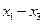по каждой группе. Результаты расчета сведены в табл.9.

Таблица 9

Групповые средние величины признаков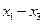

Номер группы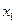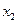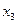
	3946,67	2166,67	5,33
	5250,00	2770,00	3,80
	6845,00	3427,14	4,00
	8499,00	4270,00	3,30
	9826,67	4583,33	3,33
	11750,00	4550,00	3,00

Средний месячный доход 3 семей первой группы (графа 2) 3946,67 руб. получен в результате усреднения их месячных доходов: (3240 + 4200 + 4400)/3 = 3946,67 руб. Аналогично рассчитанные показатели признаков 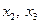представлены в графах 3,4 таблицы 9.

Рассчитаем дисперсии признаков 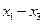, воспользовавшись формулой (5). Результаты расчета показаны в табл.10.

Таблица 10

Групповые (частные) дисперсии признаков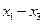

Номер группы	Показатели
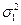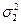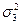	256355,36	137222,20	0,22
	118000,00	28600,00	1,36
	63750,00	79334,59	0,86
	144729,00	358600,90	1,21
	70755,56	285888,89	0,64
	62300,00	302500,00	0,00

Величина дисперсии, например, для первого признака первой группы семей 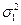рассчитывается с учетом месячных доходов семей этой группы: 3240, 4200, 4400 руб. и средней арифметической этих величин 3946,67 руб., рассчитанной в табл.9. В результате расчета получаем:

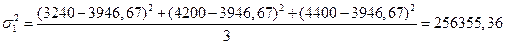руб.

Аналогично рассчитываются и другие показатели дисперси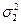и и .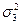

Последовательность действий при выполнении пункта 2 данной задачи следующая:

1. при заданном числе групп (10; 5) определяем равное число единиц наблюдения в каждой группе:

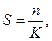
где 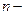число единиц совокупности (число единиц наблюдения); 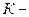число групп.

Например, при числе единиц совокупности 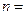30 и заданном числе групп 10 получим число единиц совокупности (семей) в каждой из 10 групп:

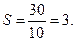
2. по данным промежуточной таблицы, в которой ранжирован по возрастанию признак 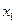, определяются (фиксируются ) соответствующие значения интервалов изменения доходов семей.

Например, при образовании 10 групп из 3 семей (признаков) нижней границей интервала для первой группы будет величина месячных доходов 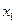= 3240 руб., а верхней границей – 4400 руб. Нижней границей интервала для второй группы будет величина свыше 4400 руб., а верхней границей величина 5250 руб. и т.д.

2. итоговые обобщающие показатели в абсолютных и относительных единицах рассчитываются по уже сформулированным правилам. Ниже для иллюстрации приводятся результаты расчета по пункту 2, представленные в таблицах 11 и 12.

Таблица 11