Установление истинности сложных высказываний.
I. Беседа с учащимися (файл MATLOG1.PPT)
II. Устная работа.
Высказывания. Простые и сложные высказывания.
1. Какие предложения являются высказываниями?
а) 3+2=5;
б) Не шуметь!
в) y2= 0;
г) Окружностью называется множество всех точек на плоскости, расстояние которых до данной точки этой плоскости имеет заданную величину.
д) Число символов в этом предложении равно 7.
е) 3 < 2;
ж) Войдите!
2. Установите: какие из следующих предложений являются
истинными, а какие - ложными высказываниями:
а) "Число 123 меньше числа -124".
б) "Все треугольники равнобедренные".
в) "Сумма чисел 4 и z равна 15".
г) "(13-2*4)*4=-7".
3. Даны высказывания:
A: "Математическая логика - важная наука"
B: "ВТ построена на законах математической логики"
Образуйте из данных высказываний сложные и подчеркните
слова, при помощи которых они образованы.
4. Среди приведенных ниже высказываний укажите сложные;
выделите в них простые, обозначив каждое из них буквой.
Запишите с помощью букв каждое сложное высказывание.
а) "На уроке логики учащиеся отвечали на вопросы учителя и
писали самостоятельную работу".
б) "Мы пойдем кататься на коньках или на лыжах".
в) "Если в данном четырехугольнике диагонали имеют равную
длину, то этот четырехугольник - ромб".
г) "-17<=0".
д) "Число 15 делится на 3 тогда и только тогда, когда сумма
цифр этого числа делится на 3".
Основные операции алгебры логики.
1. Даны простые высказывания:
А: "Петя умеет плавать"
В: "Сергей умеет прыгать"
С: "Алеша умеет стрелять"
Даны формулы сложных высказываний, составленные из этих простых. Прочтите их, используя смысл каждого простого высказывания:
2. Даны простые высказывания:
А: "Данное число не кратное 3"
В: "Данное число больше 50"
Прочтите сложные высказывания:
3. Прочтите формулы:
4. В состав истинного логического произведения входят три простых высказывания - A,B,C. Известно, что A и B - истинны. Может ли высказывание C быть одним из следующих:
а) "Дважды два равно семи".
б) "Слоны живут в Африке и Индии".
в) "5x + 3 = 11x".
5. Дано высказывание: " Иванов является членом сборной команды "Алгоритм". Какое из следующих высказываний есть логическим отрицанием данного?
а). Не Иванов является членом сборной команды "Алгоритм".
б). Иванов является членом сборной команды не "Алгоритм".
в). Иванов не является членом сборной команды "Алгоритм".
г). Неверно, что Иванов является членом сборной команды
"Алгоритм".
6. Определите значения истинности высказываний:
III. Домашнее задание.
1. Выучить конспект.
2. Ответы на вопросы:
1. Что изучает формальная логика?
2. Что изучает математическая логика?
3. Изложите основные этапы развития логики.
4. Области применения математической логики.
5. Что такое высказывание?
6. Какие высказывания бывают?
7. Какие высказывания называются простыми, а какие - сложными?
8. Что не является высказыванием?
9. Основные логические операции и их свойства.
ТАБЛИЦЫ ИСТИННОСТИ. ЭКВИВАЛЕНТНЫЕ ВЫСКАЗЫВАНИЯ.
Ход урока.
Актуализация опорных знаний.
А) Беседа.
- Что изучает формальная логика?
- Что изучает математическая логика?
- Изложите основные этапы развития логики.
- Области применения математической логики.
- Что такое высказывание?
- Какие высказывания бывают?
- Какие высказывания называются простыми, а какие - сложными?
Что не является высказыванием?
Основные логические операции и их свойства.
Б) Тест.
Вопросов
- Кто является основоположником математической логики:
- Аристотель;
- Декарт Рене;
- Лейбниц Г.В.;
- Джордж Буль.
4 - Слово "логика" обозначает
- форму мышления, в которой отражаются признаки предмета;
- совокупность правил, которым подчиняется процесс мышления;
- мысль, к которой что-то утверждается или отрицается;
- прием мышления, когда из исходного знания получается новое знание.
2 - Понятие - это ...
- форму мышления, в которой отражаются существенные признаки предмета;
- совокупность правил, которым подчиняется процесс мышления;
- мысль, к которой что-то утверждается или отрицается;
- прием мышления, когда из исходного знания получается новое знание.
1 - Суждение - это ...
- форму мышления, в которой отражаются признаки предмета;
- совокупность правил, которым подчиняется процесс мышления;
- мысль, к которой что-то утверждается или отрицается;
- прием мышления, когда из исходного знания получается новое знание.
3 - Умозаключение - это ...
- форму мышления, в которой отражаются признаки предмета;
- совокупность правил, которым подчиняется процесс мышления;
- мысль, к которой что-то утверждается или отрицается;
- прием мышления, когда из исходного знания получается новое знание.
4 - Наука о законах и формах правильного мышления - это
- женская логика;
- формальная логика;
- шахматная логика;
- математическая логика.
2 - Наука о логических связях и отношениях, лежащих в основе дедуктивного вывода - это
- женская логика;
- формальная логика;
- шахматная логика;
- математическая логика.
4 - Рассуждение, в котором из заданных двух суждений выводится третье - это
- высказывание;
- силлогизм;
- понятие;
- логика.
2 - Повествовательное предложение, относительно которого можно сказать истинно оно или ложно - это ...
- высказывание;
- силлогизм;
- понятие;
- логика.
1 - Логическая операция, соответствующая союзу "И" - это
- импликация;
- эквиваленция;
- дизъюнкция;
- конъюнкция.
4 - Логическая операция, соответствующая союзу "ИЛИ" - это
- импликация;
- эквиваленция;
- дизъюнкция;
- конъюнкция.
3 - Логическая операция, соответствующая союзу "ЕСЛИ..., ТО..." - это
- импликация;
- эквиваленция;
- дизъюнкция;
- конъюнкция.
1 - Логическая операция, соответствующая союзу "ТОГДА И ТОЛЬКО ТОГДА, КОГДА" - это
- импликация;
- эквиваленция;
- дизъюнкция;
- конъюнкция.
2 - Кто предложил использовать аппарат логики для описания электронно-ламповых схем?
- Порецкий П.С.;
- Клод Шеннон;
- Аугустус де Морган;
- Пирс Ч.С.
2 - Кто предложил использовать в логике двоичную систему счисления?
- Аристотель;
- Декарт Рене;
- Лейбниц Г.В.;
- Джордж Буль.
3 - Логическая операция ... истинна всегда, кроме случая, когда оба высказывания ложны:
- импликация;
- эквиваленция;
- дизъюнкция;
- конъюнкция.
3 - Логическая операция ... истинна только в случае, когда оба высказывания истинны:
- импликация;
- эквиваленция;
- дизъюнкция;
- конъюнкция.
4 - Логическая операция ... истинна всегда, кроме случая, когда А истинно, а В - ложно:
- импликация;
- эквиваленция;
- дизъюнкция;
- конъюнкция.
1 - Логическая операция ... истинна, когда оба высказывания ложны или истинны:
- импликация;
- эквиваленция;
- дизъюнкция;
- конъюнкция.
2 - Предложение "Неверно что, Юра занимается теннисом" соответствует логической операции
- импликация;
- эквиваленция;
- инверсия;
- конъюнкция.
3
«5» - 18, 19, 20
«4» - 14, 15, 16, 17
«3» - 10, 11, 12, 13
«2» - 9
Новый материал.
Таблица истинности - это таблица, устанавливающая соответствие между всеми возможными наборами логических переменных, входящих в логическую функцию и значениями функции.
Таблицы истинности применяются для:
- вычисления истинности сложных высказываний;
- установления эквивалентности высказываний;
- определения тавтологий.
Установление истинности сложных высказываний.
Пример 1. Установить истинность высказывания 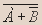 · С
· С
Решение. В состав сложного высказывания входят 3 простых высказывания: А, В, С. В таблице заполняются колонки значениями (0, 1). Указываются все возможные ситуации. Простые высказывания от сложных отделяются двойной вертикальной чертой.
При составлении таблицы надо следить за тем, чтобы не перепутать порядок действий; заполняя столбцы, следует двигаться “изнутри наружу”, т.е. от элементарных формул к более и более сложным; столбец, заполняемый последним, содержит значения исходной формулы.
| А | В | С | 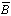 | А+ 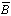 | 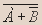 | 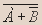 · С · С |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 |
Из таблицы видно, что данное высказывание истинно только в случае, когда А=0, В=1, С=1. Во всех остальных случаях оно ложно.
