Построение логической схемы по таблице истинности
Отчёт
Лабораторной работе №1
Вариант 18.
По дисциплине: Информационные технологии на химических производствах.
(наименование учебной дисциплины согласно учебному плану)
Тема: Построение в программном пакете Logic Works логических элементов и схем с использованием основных булевых элементов “И”, “ИЛИ” и “НЕ”.
Выполнил: студент группы ОНГ-09-2 Николаев Д.С.
Проверила: ассистент Котелева Н.И.
Санкт-Петербург
2012 год.
Цель работы
Цель работы – научиться применять Программный пакет Logic Works для реализации логической диаграммы по булевой функции от нескольких переменных, заданной в виде таблицы истинности.
Основы теории информации
Теория информации – раздел математики, исследующий процесс хранения, преобразования и передачи информации.
Теория информации изучает количественные закономерности, связанные с получением, передачей, обработкой и хранением сведений. Эти сведения (информация) представляются в форме сообщений, которые для передачи по соответствующему адресу должны быть преобразованы в последовательность сигналов, характеризуемых теми или иными признаками.
Какую бы информацию компьютер ни воспринимал, ни обрабатывал и ни выводил, он всегда превращает ее в так называемую бинарную или двоичную информацию. Она представляется всего двумя уровнями некоего сигнала - условным наличием его или отсутствием. Их называют логическая единица и нуль (1 и 0), ДА и НЕТ, True и False и т.д. Единица двоичной информации получила название бит. Два бита дают уже 4 разряда информации (22), а 8 - 256 (28).
Бит это единица двоичной информации с логическими значениями «ДА» и «НЕТ». А вот байт – восемь бит – единица информации, имеющая 28=256 значений от 0 до 255. Впрочем, биты и байты довольно малые по объему единицы информации. Поэтому широко применяются и другие единицы информации: килобит (кбит, или 1024 бит), килобайт (кбайт, или 1024 байт), мегабит (Мбит, 1024 кбит), мегабайт (Мбайт, 1024 кбайт) и т.д.
Логические элементы и основные понятия Булевой алгебры.
Логические элементы — устройства, предназначенные для обработки информации в цифровой форме (последовательности сигналов высокого — «1» и низкого — «0» уровней в двоичной логике, последовательность "0", "1" и "2" в троичной логике, последовательности "0", "1", "2", "3", "4", "5", "6", "7", "8"и "9" в десятичной логике). Физически логические элементы могут быть выполнены механическими, электромеханическими (на электромагнитных реле), электронными (на диодах и транзисторах), пневматическими, гидравлическими, оптическими и др.
С развитием электротехники от механических логических элементов перешли к электромеханическим логическим элементам (на электромагнитных реле), а затем к электронным логическим элементам на электронных лампах, позже - на транзисторах. После доказательства в 1946 г. теоремы Джона фон Неймана о экономичности показательных позиционных систем счисления стало известно о преимуществах двоичной и троичной систем счисления по сравнению с десятичной системой счисления. От десятичных логических элементов перешли к двоичным логическим элементам. Двоичность и троичность позволяет значительно сократить количество операций и элементов, выполняющих эту обработку, по сравнению с десятичными логическими элементами.
Логические элементы выполняют логическую функцию (операцию) с входными сигналами (операндами, данными).
Логические операции (булева функция) своё теоретическое обоснование получили в алгебре логики (Булевой алгебры). Наиболее известными операциями булевой алгебры являются: конъюнкция, дизъюнкция, импликация, эквивалентность, отрицание. В таблице 1 и на рисунке 1 представлены обозначения операций Булевой алгебры в различных отраслях применения, а также пояснения некоторых операций.
Табл.1. Обозначения основных операций Булевой алгебры в различных областях применения.
| Название | конъюнкция логическое И | дизъюнкция логическое ИЛИ | отрицание,инверсия логическое НЕ | сложение по модулю 2 исключающее ИЛИ |
| Область применения обозначений | ||||
| Булева алгебра | x • y | x + y | 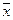 | x 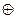 y y |
| Булева алгебра | x y | x 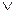 y y | 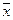 | x 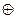 y y |
| Булева алгебра | x 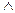 y y | x 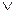 y y | 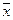 | x Ф y |
| Логика | x & y | x V y | ┐x | |
| Теория множеств | x 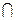 y пересечение y пересечение | x 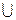 y объединение y объединение | 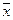 дополнение до 1 дополнение до 1 | |
| Языки программирования | x AND y | x OR y | NOT x | x XOR y |
| Язык Си (логические) | x && y | x || y | !x | |
| Язык Си (поразрядные) | x & y | x | y | -x (обратный код) | x - y |
Построение логической схемы по таблице истинности.
Таблица, в которой задано значение функции F для всех возможных комбинаций входных сигналов, называется таблицей истинности булевой функции. Число возможных комбинаций входных сигналов вычисляется по формуле 2N, где N-число входов.
Например, пусть имеется таблица истинности для некоторой функции от двух входов x и y.
| X | Y | F |
Требуется записать Булево (логическое) выражение по данной таблице истинности. Существуют два эквивалентных стандартных способа построения логического выражения:
1)стандартная сумма произведений (каноническая сумма минитермов);
| X | Y | F | минитермы (произведения) |
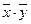 | |||
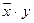 | |||
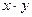 |
Минитермы записываются для всех строчек таблицы, содержащих "1" в столбце значений функции, а затем составляется их сумма. Инверсия ставится над буквой (литералом), обозначающей переменную, если значение переменной в данной строчке таблицы равно "0".
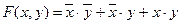 -стандартная сумма произведений (каноническая сумма минитермов)
-стандартная сумма произведений (каноническая сумма минитермов)
Данной формуле соответствует следующая логическая диаграмма или схема в Logic Works.
Построение логической диаграммы следует начинать с конца , то есть выхода схемы.
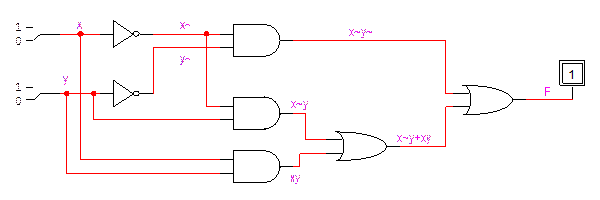
2) стандартное произведение сумм (каноническое произведение макстермов).
Макстермы записываются для всех строчек таблицы, содержащих "0" в столбце значений функции, а затем составляется их произведение. . Инверсия ставится над буквой (литералом), обозначающей переменную, если значение переменной в данной строчке таблицы равно "1".
| X | Y | F | Макстермы (суммы) |
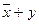 | |||
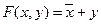 -стандартное произведение сумм (каноническое произведение макстермов)
-стандартное произведение сумм (каноническое произведение макстермов)
Данной формуле соответствует следующая логическая диаграмма или схема в Logic Works.
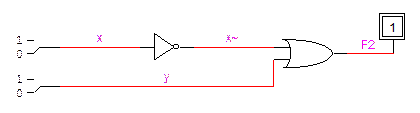
Какая из схем будет проще, зависит от числа "1" и "0" в таблице истинности.
Для того, чтоб убедиться в эквивалентности полученных формул, совместите обе схемы на одном листе Logic Works и используйте общие входные ключи.
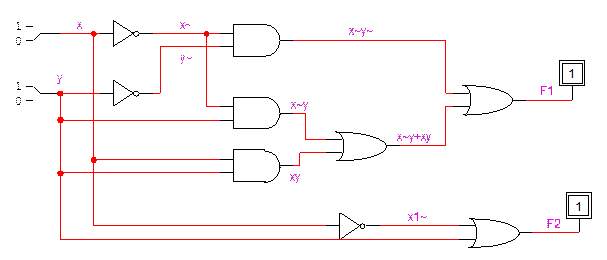
Не используйте одинаковые обозначения для различных линий сигналов на схеме!
