Обеспечения контроля работы автомата

Помехоустойчивое кодирование. Коды по их отношению к качеству передаваемой связи можно разделить на те, которые обнаруживают ошибки и те, которые их исправляют с большой степенью вероятности. В задачи помехоустойчивого кодирования входит обнаружение и исправление ошибок, связанных с неисправностями в работе ЭВМ (помехами). Для выявления ошибок в процессе передачи закодированной информации необходимо ввести информационную избыточность.

Пусть имеется сообщение (а₁а₂…а_m) в виде двоичного кортежа длины m. Эта последовательность, состоящая из m нулей и единиц, кодируется двоичным кортежем длины n (n>m). Сообщение передаются по каналу связи, в котором действует источник помех.При передаче кода (b₁b₂…b_n)по каналу связи код, сообщение может значительно исказиться. Тогда на выходе получают слово (b'₁b'₂…b'_n), отличающееся от (b₁b₂…b_n) не более, чем в p позициях.

Проблема заключается в построении самокорректирующегося кода (b₁b₂…b_n), который по любому его исходному слову (а₁а₂…а_m), позволит на выходе получить такой кортеж b'₁b'₂…b'_{n ,} который сможет однозначно восстановить передаваемый код b₁b₂…b_n, и получить исходное сообщение а₁а₂…а_m. Коды, обладающие такой способностью, называют самокорректирующимися кодами относительно источника помех или кодами, исправляющими p ошибок.

Пусть заданы алфавитыА=В={0,1}, а кодирование выполняется без дополнительных помех. Возможны три типа ошибок:

1. 0→1, 1→0 - ошибки замещения разряда;

2. 0→۸, 1→۸ - ошибки выпадания разряда;

3. ۸→1, ۸→0 — ошибки вставки разряда.

Один из способов обнаружения одиночной ошибки заключается в удвоении каждого передаваемого символа. Для исправления одиночной ошибки длина слова утраивается.

Например, слово «март» можно закодировать в слово «ммаарртт». Тогда, в случае искажения одного из символов, ошибку можно обнаружить по второму, неискаженному символу. Например, получив искаженное слово «ММаарртс» мы должны проверить оба варианта гипотез: «Марс» и «Март».

Весомкодовой комбинации V(А) называют количество единиц в кодовой комбинации.

Каждое из слов X=(x₁,x₂,…,x_n) длины n в этом алфавите обозначим Bⁿ отождествим с n-мерным вектором, который может быть разложен по базисным векторам в этом n-мерным векторном пространстве Bⁿ: .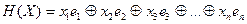

Расстоянием Хемминга (или кодовым расстоянием) между словами A и B называется вес третьей кодовой комбинации, полученной при сложении исходных по модулю 2. Тогда расстояние Хемминга равно d(A,B)=AÅB. Заметим, что расстояние Хемминга равно числу несовпадающих позиций (разрядов) при сравнении их двоичной записи. Для произвольного кода X=(x₀,x₁,…,x_n-1)Í Bⁿ расстояние Хемминга равно

d(X)=min d(xi, xj)

Код позволяет обнаружить не более k ошибок тогда и только тогда, когда минимальное расстояние Хемминга между кодовыми словами превосходит k,т.е.когда d(b_i,b_j)³ k+1.

Код позволяет исправить не более k ошибок тогда, и только тогда, когда минимальное расстояние Хемминга между кодовыми словами превосходит 2k, т.е.когда d(b_i,b_j)³ 2k+1.

Очевидно, что сумма всех букв закодированного слова сообщения, передаваемого с помощью М2 должна быть равной 0. Отсутствие нуля при получении этого сообщения свидетельствует об однократной ошибке, которую можно исправить. Однако код с проверкой на четность не сможет обнаружить двукратную ошибку.

Механизм действия помех на кодовые слова из 0 и 1 математически описывается операцией "сумма по модулю 2". Обозначим наличие ошибки в данной позиции через "1", а ее отсутствие "0". Замена символа за счет помех ("0" на "1" или "1" на "0") определяется с помощью математического действия сумма по модулю два:

0 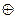0=0 - передавали 0, ошибки нет, получили 0;

0 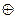1=1 - передавали 0, ошибка есть, получили 1;

1 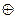0=1 - передавали 1, ошибки нет, получили 1;

1 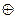1=0 - передавали 1, ошибка есть, получили 0.

Пусть передавали двоичное слово 101001 - а получили 110001, т.е. ошибка произошла на втором и третьем разряде.

Если такая ошибка произойдет повторно, то восстановится исходное сообщение.

Действительно,

в первый раз: во второй раз:

передавали 101001 передавали 110001

ошибка 011000ошибка 011000

получили 110001 получили 101001

Так совпали первое слово при передаче в первом сообщении и последнее слово при передаче во втором сообщении, то первоначальное сообщение восстановлено: две одинаковые ошибки взаимно уничтожили друг друга.

4) Коды Хемминга.Коды Хемминга – это (m,n)-код, где обозначает n - длину кодового слова, m - число информационных символов. Такой код содержит всего 2^m слов длиной m. Вместо того, чтобы перечислять все возможные кодовые слова в виде множества, применяется более компактный (экономный) способ задания матрицей.

Для (m,n)-кодов требуется выполнение соотношений: n=m+r, где 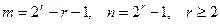, что позволяет исправить однократную ошибку с помощью введения r дополнительных (контрольных) символов методами матричного кодирования. Тогда в каждом кодовом слове b=b₁b₂…b_n символы с индексами, равными степеням числа 2 будут контрольными, а все остальные – информационными. Так, для (4,7)-кода в любом кодовом слове b=(b₁b₂b₃b₄b₅b₆b₇) символы b₁b₂ b₃ являются контрольными, а b₃ b₅b₆b₇ – информационными.

Проверочной матрицей М (m,n)-кода Хемминга называется матрица

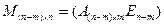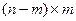или M=(А Е) размера , где E– единичная матрица порядка n-m, а матрица А размера подбирается так, чтобы в столбцах матрицы М были указаны все двоичные разложения чисел от 1 до n. Порядок составления столбцов матрицы А произволен, но ни один набор не повторяется.

Порождающей матрицей 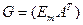называется матрица, составленная из матрицы E_m – единичной матрицы m порядка и матрицы 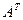– полученной транспонированием матрицы A (строки и столбцы меняются местами).

Для того, чтобы закодировать некоторое кодовое слово α, представленное в виде вектора-строки, надо его умножить на порождающую матрицу G. Первые m букв вектора αG образуют исходное сообщение, последние n–m букв используются для контроля.

Опишем механизм исправление однократной ошибки с помощью кода Хемминга.

Пусть полученное некое кодированное сообщение b. Если при умножении проверочной матрицы М на вектор 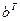образуется нулевой вектор М 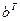, то говорят, что полученное сообщение не содержит ошибок. Если в процессе умножения проверочной матрицы М на вектор 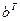образуется ненулевой вектор М 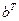, то говорят, что полученное сообщение содержит ошибки. Для их устранения надо изменить символ в том разряде (позиции), номер которой равен номеру столбца проверочной матрицы М, совпадающего с вектором М .

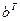При декодировании первые m символов образуют исходное сообщение.

Код Хемминга может быть получен и в векторной форме. Пусть известна n – длина кодового слова (b₁b₂…b_n), 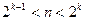где 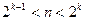(k<n). Произвольному двоичному слову-вектору b=(b₁b₂…b_n)ÎBⁿ поставим в соответствие некоторую функцию H(b) – его разложение по единичным векторам e_k, которое имеет вид: 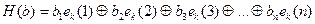. Тогда H(b) есть вектор длины n, полученный при сложении по модулю 2 векторов e_k, которые являются двоичными записями с помощью k символов номеров единичных знаков заданного слова. Такая функция при подстановке значений аргументов на множестве Bⁿ принимает некоторые фиксированные значения.

Теорема.Код Хемминга H(b), состоящий из всех слов b=(b₁b₂…b_n)ÎBⁿ, таких, что H(b)=(0,0,…,0), является кодом с исправлением одного замещения.

Тогда, в результате одиночной ошибки значение функции изменяется, причем, если в слове b произошло замещение одного из символов, то координаты полученного вектора H(b) соответствуют двоичной форме замещенного разряда.

Контроль по четности. Для обнаружения однократной ошибки и ее исправления применяется контроль по четности, который заключается в том, что сумма двоичных единиц в машинном слове, включая контрольный разряд, должна иметь определенную четность, т.е. быть либо всегда четной, либо всегда нечетной.Кодирование с использованием проверки по четности заключается в добавлении сообщению в виде слова длины m из символов 0 и 1 дополнительного символа, который равен сумме по модулю 2 всех символов этого передаваемого слова длины m. Декодирование полученного сообщения сводится к отбрасыванию последней цифры.Такойкод с проверкой четности сможет обнаружить ошибку, но не сможет ее устранить.

Для уменьшения вероятности ошибки в двоичных кодах используют код Грея, в котором каждые две позиции отличаются только одним разрядом, т.е. на 1 бит. Поэтому выходной сигнал может быть представлен лишь одним из двух состояний: истинный или ложный. Код Грея тоже использует лишь два знака 0 и 1, но соседние числа отличаются только в одном разряде, т.е. на 1 бит информации.