В) Метод обобщения

Суть его в следующем:

1. Исходной теорией является теория, законы которой могут быть записаны на логико-математическом (или ином точно построенном) языке. Эти законы рассматриваются с точностью до математической семантики, т.е. в отвлечении от специфической частно-научной семантики. Например, возьмем закон ньютоновой механики 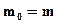, который сообщает о том, что масса тела в инерциальной системе отсчета (в которой тело движется) 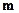равна его массе в собственной системе отсчета (в которой тело покоится) 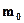. Рассмотрим этот закон с точностью до математической семантики. Тем самым отвлечемся от того, что это физические величины - массы. Тогда они предстанут просто как математические величины - переменные для действительных чисел. 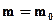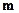И закон превратится в математическое уравнение , где и 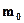- переменные для чисел, и только.

2. Полученные математические уравнения обобщаются с помощью математических тождественных преобразований и метода обобщениялогики. Так, формулу 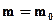можно с помощью тождественных преобразований и обобщения привести к виду

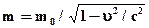. Это делается так: 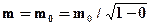. Затем число 0 заменяется по правилу обобщения на переменную 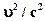, частным случаем которой оно является, и получается формула .

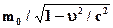3. Получившимся в результате обобщения уравнениям придается новая интерпретация, в результате чего строится новая теория. В нашем случае уравнению 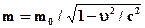придается релятивистская интерпретация символам массы, скорости 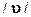и постоянной скорости света 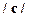. В итоге получим закон релятивистской механики из исходного закона ньютоновой механики.

По методам пролиферации, эффективизации и обобщения (а также и другим, которые здесь не были упомянуты) практически каждый может строить новые геометрии, физики и другие теории. Но будут ли они приняты? Этот вопрос можно решить лишь демонстрацией того, что созданная теория может решать такие научно-практические задачи, которые не решала прежняя теория или решала их хуже. Прагматический критерий в решении этой проблемы является определяющим. Поэтому рассмотренные методы построения новых теорий весьма полезны в качестве эвристических методов. Строя с их помощью теории и проверяя их на практическую применимость, можно построить теорию, которая будет принята в число научных теорий.

[1] Ю.А. Петров Культура мышления.М., 1990 ; Его же. Азбука логичного мышления. М., 1991. Данная часть работы оформлена в виде последовательности действий в следующем пособии : Захаров А.А., Захарова Т.Г. Дневник аспиранта. Озерск : МИФИ. 1997. - 57 с.