Шестнадцатеричная позиционная система счисления
В шестнадцатеричной позиционной системе счисления для записи произвольных чисел используются шестнадцать цифр, десять из которых от 0 до 9 по изображению совпадают с арабскими цифрами, а для изображения оставшихся шести обычно используют латинские буквы от 
до 
. Таким образом, ряд шестнадцатеричных цифр имеет вид 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F.
Основание системы счисления (число шестнадцать) записывается двумя цифрами в виде 
. Любые числа шестнадцатеричной системы счисления представляются в виде последовательности шестнадцатеричных цифр.
Например, десятеричное число 
в шестнадцатеричной системе счисления будет записано с точностью до четвертого знака после запятой следующим образом:
(здесь 10 означает число 16) и все операции должны выполняться в шестнадцатеричной системе счисления.
Правильность изображения в шестнадцатеричной системе десятичного числа легко проверить, переписав правую часть равенства 
в десятеричной системе счисления, помня, что 
, и произведя в этой системе соответствующие арифметические операции с учетом оговоренной выше точности перевода дробной части. Проделав все это, получим:
.
Сложение, вычитание, умножение и деление шестнадцатеричных чисел производится по тем же правилам, что и в десятичной системе счисления. При этом, однако, следует пользоваться шестнадцатеричными таблицами сложения-вычитания (табл. 1.6) и умножения (табл. 1.7).
Правила пользования этими таблицами аналогичны правилам пользования соответствующими восьмеричными таблицами.
Примеры:
Сложение Вычитание
A2C, F47 F13, 7F4
+ 8B1, D98 – 3D4, E2F
12DE, CDF B3E, 9C5
Таблица 1.6
Таблица сложения - вычитания шестнадцатеричных чисел
| + – | A | B | С | D | E | F | ||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | A | B | C | D | E | F | ||||||||||
| B | B | C | D | E | F | 1A | ||||||||||
| C | C | D | E | F | 1A | 1B | ||||||||||
| D | D | E | F | 1A | 1B | 1C | ||||||||||
| E | E | F | 1A | 1B | 1C | 1D | ||||||||||
| F | F | 1A | 1B | 1C | 1D | 1E |
Таблица 1.7
Таблица умножения шестнадцатеричных чисел
| х | A | B | C | D | E | F | ||||||||||
| A | B | C | D | E | F | |||||||||||
| A | C | E | 1A | 1C | 1E | |||||||||||
| C | F | 1B | 1E | 2A | 2D | |||||||||||
| C | 1C | 2C | 3C | |||||||||||||
| A | F | 1E | 2D | 3C | 4B | |||||||||||
| C | 1E | 2A | 3C | 4E | 5A | |||||||||||
| E | 1C | 2A | 3F | 5B | ||||||||||||
| 1B | 2D | 3F | 5B | 5A | 6C | 7E | ||||||||||
| A | A | 1E | 3C | 6A | 6E | 8C | ||||||||||
| B | B | 2C | 4D | 6E | 8F | 9A | A5 | |||||||||
| C | C | 3C | 9C | A8 | B4 | |||||||||||
| D | D | 1A | 4E | 5B | 8F | 9C | A9 | B6 | C3 | |||||||
| E | E | 1C | 2A | 7E | 8C | 9A | A8 | B6 | C4 | D2 | ||||||
| F | F | 1E | 2D | 3C | 4B | 5A | A5 | B4 | C3 | D2 | E1 |
Примеры:
Умножение Деление
|
3E5, F4 = B4A, 2F.
1 FF9, FC Все операции производятся в
шестнадцатеричной системе счисления
Для наглядности и удобства пользования в дальнейшем сведем в одну таблицу числа, представленные в рассмотренных выше системах счисления в диапазоне от 0 до 20 (табл.18).
Таблица 1.8
| Десятичная система | Двоичная система | Восьмеричная система | Шестнадцатеричная система |
| A | |||
| B | |||
| C | |||
| D | |||
| E | |||
| F | |||
Перевод чисел из одной позиционной системы счисления в другую
Перевод целых чисел
Пусть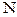 
- целое число, записанное в системе счисления с основанием 
.
Пусть 
- основание другой системы счисления, записанное в исходной -ичной системе счисления, причем 
.
Требуется перевести число 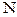из системы счисления с основанием в систему счисления с основанием 
.
Предположим, что изображение числа 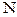в -ичной системе счисления найдено и имеет следующий вид:
, (1.1)
где 
- цифры -ичной системы, а 10 – основание этой системы, т.е. .
С учетом того, что 
, а 
, заменим в правой части равенства (1.1) числа и 10 их -ичными изображениями 
и . Тогда получим:
. (1.2)
Деля обе части равенства (1.2) на , имеем:
, (1.3)
где 
представляет собой правильную дробь, поскольку 
.
Из равенства (1.3) видно, что при делении числ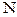а на остаток равен 
, а частным будет
.
Если теперь частное 
разделить на , то получим в остатке 
, а в новом частном
.
Выполняя этот процесс деления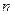 
раз, можно последовательно найти все числа 
, причем последнее частное будет иметь вид
.
Из сказанного вытекает следующее общее правило перевода целых чисел 
из одной позиционной системы счисления в другую для любых оснований и .
Правило перевода.Путем последовательного деления числа 
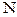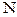и его частных на получают в виде остатков деления -ичные записи -ичных цифр (начиная с младшей), необходимые для изображения числа в -ичной системе счисления. Последовательное деление производится до тех пор, пока не получится частное, меньшее чем . Это последнее частное является старшей -ичной цифрой числа . Деление выполняется в исходной, т.е. в -ичной системе счисления.
Пример.
Пусть 
.
Требуется перевести десятичное число 
в двоичную систему счисления, т.е. найти число 
.
Операция Частное Остаток
189 : 2 = 94 + 1
94 : 2 = 47 + 0
47 : 2 = 23 + 1
23 : 2 = 11 + 1
11 : 2 = 5 + 1
5 : 2 = 2 + 1
2 : 2 = 1 + 0
1
Таким образом, двоичная запись десятичного числа 
имеет следующий вид: 
.
Проверка правильности перевода:
.
Пример.
Пусть 
.
Требуется перевести десятичное число в восьмеричную систему счисления, т.е. найти число 
.
Операция Частное Остаток
189 : 8 = 23 + 5
23 : 8 = 2 + 7
2
Таким образом, восьмеричная запись числа имеет следующий вид: 
.
Проверка правильности перевода:
.
Перевод правильных дробей
Пусть 
- правильная дробь, записанная в системе счисления с основанием . Пусть - основание другой системы счисления, записанное в исходной -ичной системе счисления, причем .
Требуется перевести правильную дробь из системы счисления с основанием в систему счисления с основанием , т.е. 
.
Предположим, что изображение правильной дроби в -ичной системе счисления найдено и имеет следующий вид:
, (1.4)
где 
-ичные цифры, а 10 - основание системы счисления, т.е. .
Заменяя входящие в правую часть равенства (1.4) числа 
и 10 их -ичными изображениями 
и , получим
. (1.5)
Умножая обе части равенства (1.5) на , имеем
. (1.6)
Целая часть числа (1.6) равна 
, а его дробной частью является
.
Умножая новую дробь 
на , получим число, целая часть которого равна 
, а дробная часть имеет вид
.
Повторяя описанный процесс умножения нужное количество раз, легко найти одну за другой (в -ичной записи) -ичные цифры, начиная со старшей, необходимые для изображения числа с заданной точностью.
Из сказанного следует общее правило перевода правильных дробей 
из одной позиционной системы счисления в другую для любых оснований и .
Правило перевода.Путем последовательного умножения числа 
и дробных частей образующихся произведений на получают в виде целых частей этих произведений -ичные записи -ичных цифр (начиная со старшей), необходимых для изображения правильной дроби в системе счисления с основанием . Умножение выполняется в исходной, т.е. в -ичной системе счисления до тех пор, пока не будет получена заданная точность перевода, либо дробная часть произведения не станет равной нулю.
Пример.
Пусть 
.
Требуется перевести правильную десятичную дробь 
в двоичную систему счисления, т.е. найти число 
.
Целая Дробная
Часть часть
| 0, |
| ||
| 1, |
| ||
| 0, |
| ||
| 1, |
| ||
| 1, |
Двоичная запись десятичной правильной дроби 
имеет следующий вид: 
.
Проверка правильности перевода:
.
Пример.
Пусть 
.
Требуется перевести десятичную дробь в восьмеричную систему счисления, т.е. найти число 
.
Целая Дробная
Часть часть
| 0, |
| ||
| 5, |
| ||
| 4, |
Восьмеричная запись десятичной правильной дроби 
имеет следующий вид: 
.
Проверка правильности перевода:
.