Последовательность синтеза методом упрощения логических выражений

Лекция №11

Набор функциональных узлов образует так называемые логические серии.

Три основные логические серии, различающиеся по схемотехнике базового элемента (вентиля):
- ТТЛ (транзисторно-транзисторная логика);
- ЭСЛ (эммитерно-связанная логика);
- КМОП (комплиментарная, металл-окисел-проводник логика)

Существует много вариаций этих основных серий.

Они отличаются:

- по уровням входных и выходных сигналов:

- быстродействию;

- потребляемой мощности и пр.

Они отличаются также по конструкции корпуса и номенклатуре функциональных узлов в серии.

Основные законы алгебры логики

Дизъюнктивная форма Коньюктивная форма

1. Переместительный
x₁+x₂=x₂+x₁ x₁*x₂=x₂*x₁

2. Сочетательный
(x₁+x₂)+x₃=x₁+(x₂+x₃) (x₁*x₂)*x₃=x₁*(x₂*x₃)

3. Распределительный
x₁*(x₂+x₃)=x₁*x₂+x1*x3

Первые три существуют и в алгебре чисел.

4. Поглощения
x₁+x₁*x₂=x₁(1+x₂)=x₁ x₁(x₁+x₂)=x₁

5. Склеивание
x₁*x₂+x₁* 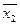=x₁ ( x₁+x₂)+(x₁+ 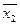)=x₁

6. Отрицание де Моргана

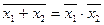
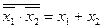
Понятие о синтезе комбинационных цепей

Комбинационные логические цепи- цепи у которых выходные сигналы однозначно зависят от входных сигналов и не зависят от предыстории.

Их называют автоматами без памяти. Аппараты без памяти – вектор сигналов на выходе зависит только от вектора сигналов на входе.

Существуют также логические аппараты с памятью.

Цель синтеза: минимизировать число логических элементов в автомате.

Оптимизация достигается:
а) упрощением логических выражений (как в алгебре) используя законы логических операций.
б) минимизация логических выражений с использованием различных формальных методов:

- метод Мак-Класки;

- минимаксный;

- метод весовых коэффициентов;

- частотно-минимаксный;

- метод диаграмм Вейча(карт Карно).

Последовательность синтеза методом упрощения логических выражений

1. Составление таблицы истинности

№	Х1	Х2	Х3	Y

Рис. 11.1

Y - логическая функция 3-х аргументов Х1, Х2, Х3

1. Составляем логическую функцию

Y= + +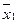

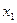
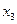
1. Упрощаем ее

Y= + + = ( + )+ = + =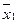

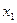
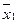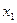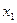
= ( + ) (10.1)

Преобразуем дальше выражение ( + ): (10.2)

+ = - склеивание (10.3)

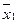
+ = - склеивание (10.4)

------------------------

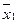
+ + + = + (10.5)

(10.5) получили сложением (10.3) и (10.4)

Преобразует 1, 2 и 4-ое слагаемые в (10.5)

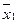
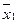+ + = ( + )+ = (1+ )= (10.6)

Подставляем (10.6) в (10.5), получим

+ = + - операция обобщенного склеивания (10.7)

Подставляем (10.7) в (10.1), получим в итоге

Y=( + ) (10.8)

Интуиция и опыт (результат зависит от квалификации)

Синтез логических выражений методом диаграмм Вейча (карт Карно)

Применим для функций до 5-6 аргументов

При минимизации с помощьюдиаграмм Вейча исходную функцию необходимо привести предварительно к ДНФ (дизъюнктивно нормальной форме), т.е. выразить в виде логической суммы простых конъюнкций.

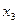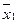
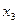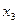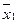
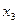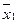
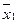
Y= + + + + + + + (10.9)

Простая конъюнкция – произведение переменных взятых с отрицанием или без в котором каждая переменная встречается не более одного раза.

Простая конъюнкцияв которую входят все аргументы рассматриваемой логической функции называется минтермом.

Если мы записываем логическую функцию исходя из таблицы истинности, то мы имеем сумму минтермов.

Алгоритм синтеза:

1) Представление функции в ДНФ

2) Построение диаграмм Вейча (таблицы) в которой число клеток равно числу возможных минтермов.

Пустьn – число аргументов, при

n =2 число клеток = 4

n =3 число клеток = 8

n =4 число клеток =16

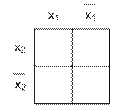
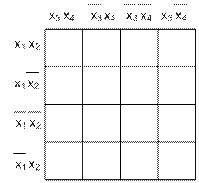
Рис. 11.2

Соседние столбцы таблиц и строки должны отличаться значением только одной переменной

Например: можно и 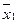, но нельзя и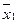

3) в таблице ставим “1” если минимизированная функция Y при заданном числе аргументов = 1 и “0” если Y=0

Наш пример: Y= + + (10.10)

Рис. 11.3

4) Обводим прямоугольным контуром все единицы- это формальный прием, по

правилам:

- контур должен быть прямоугольным;

- внутри контура – только клетки с ‘1” ;

- число клеток внутри контура 1, 2, 4, 8… ;

- крайне нижние и крайне верхние строки считаются соседними;

- крайне левая и крайне правая строки считаются соседними;

- число контуров д.б. минимальным, а их размер- максимальным;

- клетка может входить в несколько контуров.

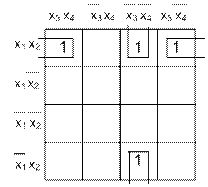
Рис. 11.4

Продолжим решение нашего примера (10.10)

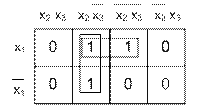
Рис. 11.5

5) Запись минимизируемой функции в виде сумм логических произведений,

описывающих эти контуры.

Y= + + + = ( + )+ ( + )

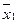= ( + ) сравнить с (10.8) (10.11)

Пример 2

№	Х1	Х2	Х3	Y

Рис. 11.6

Y₂= + + +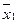

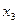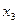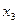
Рис. 11.7

Y₂= + + + + + = + +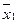

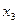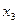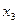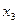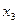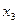Примеры показали простоту и наглядность метода минимизации с помощью диаграмм Вейча.

При n>4 наглядность метода снижается