Простые суждения. Логическая структура и виды
Простые суждения включают в себя в качестве структурных элементов: субъект, предикат, связку и кванторное слово. Субъектом суждения называется понятие, выражающее предмет суждения, т.е. это то о чем говорится в данном суждении. Обозначается в логике латинской буквой «S». Предикатом суждения называется понятие, выражающее ту или иную информацию о предмете суждения. Обозначается предикат буквой «Р». Субъект и предикат – основные элементы суждения, они называются терминамисуждения.
Связь между субъектом и предикатом, отражающая реальные отношения между мыслимыми в понятиях объектами, раскрывается посредством логической связки. В русском языке связка выражается словами: «есть» («не есть»), «является» («не является»), «имеется» («не имеется») и т.д., обозначается тире, а может подразумеваться, выражаясь согласованием слов («Идет дождь», «Собака лает»). Поскольку субъект и предикат, будучи понятиями, могут рассматриваться с точки зрения их содержания и объема, то связка может быть истолкована в содержательном и объемном планах. В содержательном она выражает принадлежность или непринадлежность признака субъекту. Со стороны объема она раскрывает включение (или исключение) подкласса в класс объектов или принадлежность (непринадлежность) элемента классу.
Кванторное слово (каждый, все, ни один, некоторый и т.д.) указывает: относится ли информация о предикате суждения ко всему объему понятия, выражающему субъект, или к его части. Например, в суждении «Всякое преступление – противоправное деяние» субъектом суждения является понятие «преступление», предикатом – «противоправное деяние», связка выражена знаком тире, а кванторное слово «всякое» указывает, что характеристика «противоправное деяние» относится ко всему объему (к каждому элементу объема) понятия «преступление».
В самом общем виде простое суждение можно выразить формулой: «S есть (не есть) Р». В современной логике «S» и «Р» называют логическими переменными, т.к. они могут вмещать в себя самое различное содержание. А связка – это логическая постоянная, поскольку в ней заключено неизменное содержание: она всякий раз служит показателем наличия или отсутствия чего-либо у предмета мысли.
Виды простых суждений
По характеру признака, выражаемого предикатом суждения, выделяют три вида простых суждений:
1. Атрибутивные – суждения, в которых признак связан с наличием или отсутствием свойства. Например: «Москва – столица России», «Студенты, как правило, находчивые люди».
2. Реляционные или с отношением – это суждения, в которых признак связан с наличием или отсутствием отношения. Например: «Лето этого года теплее лета прошлого года», «Иван выше Петра», «2 в степени три равно 8».
3. Экзистенциальные или существования– это суждения, в которых выражено существование или несуществование объектов. Например: «Да, были люди в наше время», «Безвыходных ситуаций нет».
Особое значение в логике имеет деление простых суждений на виды по характеру связки (ее качеству) и характеру субъекта (его количеству, объему).
Виды суждений по качеству. Качество суждений – одна из важнейших его логических характеристик. Под ним понимается самая общая логическая форма простых суждений: утвердительная или отрицательная. Определяется качество суждений характером связки: какая она – утвердительная или отрицательная. В зависимости от этого суждения делятся на утвердительные и отрицательные. В утвердительных суждениях раскрывается наличие какой-либо связи между субъектом или предикатом. Общая формула: «S есть Р». Например: «Студенты сдали экзамен по логике», «Киты – млекопитающие». В отрицательных суждениях, наоборот, раскрывается отсутствие той или иной связи между субъектом или предикатом. Общая формула: «S не есть Р». Например: «Студенты не сдали экзамен по логике», «Киты не рыбы». Важно уяснить, что частица «не» в отрицательных суждениях относится к связке. Если же она входит в состав предиката (или субъекта), то это означает, что предикат (субъект) выражен отрицательным (а не положительным) понятием, в целом же суждение будет утвердительным. Например: «Некоторые законы бездействуют», «Профсоюзы независимы».
Виды суждения по количеству. Количество суждений – другая важнейшая характеристика суждений. Под количеством понимается логический объем субъекта. В зависимости от этого выделяются общие, частныеи единичные суждения.
Общие суждения – это суждения, в которых предикат относится ко всему объему субъекта суждения. Показателем количества (объема) субъекта выступает кванторное слово, которое в русском языке для общих суждений выражается словами: «все», «всякий», «каждый» (если суждение утвердительное) или «ни одни», «никто», «никакой» (если суждение отрицательное) и называется квантором общности – «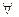 ». Формулы общих суждений: «Все S есть Р», «Ни одно S не есть Р». Например: «Все адвокаты - юристы», «Никто не хотел умирать». В мыслительной практике кванторное слово нередко опускается. В этом случае для определения количественной характеристики суждения его мысленно следует восстановить, поставив перед субъектом слово «каждый», если суждение утвердительное, или слово «ни один», если суждение отрицательное.
». Формулы общих суждений: «Все S есть Р», «Ни одно S не есть Р». Например: «Все адвокаты - юристы», «Никто не хотел умирать». В мыслительной практике кванторное слово нередко опускается. В этом случае для определения количественной характеристики суждения его мысленно следует восстановить, поставив перед субъектом слово «каждый», если суждение утвердительное, или слово «ни один», если суждение отрицательное.
Частные суждения – это суждения, в которых предмет относится лишь к части объема субъекта, лишь к некоторым его элементам. И в этом случае показателем объема субъекта выступает кванторное слово, называемое в современной логике квантором существования и обозначаемое символом «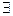 ». В русском языке он выражается такими словами как: некоторые, не все, большинство, часть и т.п. Например: «Некоторые войны справедливы», «Большинство студентов учатся добросовестно».
». В русском языке он выражается такими словами как: некоторые, не все, большинство, часть и т.п. Например: «Некоторые войны справедливы», «Большинство студентов учатся добросовестно».
Единичные суждения – это суждения, в которых субъект выражен единичным понятием, для которых в русском языке используются собственные имена или слово «это». Например: «Это – картина Шишкина», «Московский Кремль – самый красивый в мире», «Уголовный кодекс РФ давно не пересматривался». Нередко в этих случаях субъект может быть выражен собирательным понятием, например: «Большая медведица – созвездие», «Солнечная система – не единственная планетная система в нашей Галактике».
Количественная характеристика суждений имеет важное значение для уточнения, определенности наших мыслей в практике мышления. Не уточнив количество суждения нельзя осуществить ни опровержение, ни доказательство исходного суждения, ибо в зависимости от изменения количественной характеристики суждения изменяются способы его доказательства и опровержения. Так, при использовании в дискуссии, споре суждения «Человек имеет преступные наклонности», необходимо уточнение его количественной характеристики, путем приведения к одному из видов: «Этот человек имеет преступные наклонности», «Некоторые люди имеют преступные наклонности» или «Все люди имеют преступные наклонности». Понятно, что способы доказательства для них будут разными.
Суждения, у которых количество и качество может быть точно определено, называются категорическими[6] суждениями.
Качество и количество суждений тесно связаны. Поэтому в логике большое значение придается объединенной классификации категорических суждений по их количеству и качеству. При этом, единичные суждения приравниваются к общим на том основании, что те и другие высказываются обо всем объеме субъекта (Объем субъекта единичных суждений состоит из одного элемента).
Возможны четыре вида категорических суждений: общеутвердительные, общеотрицательные, частноутвердительные и частноотрицательные. Еще в средневековье в логике были введены буквенные обозначения этих четырех видов категорических суждений. Они происходят от гласных букв, входящих в латинские слова affirmo – утверждаю и nego – отрицаю. Общеутвердительные суждения получили обозначение А, общеотрицательные – Е, частноутвердительные – J, частноотрицательные – О.
Общеутвердительное суждение (А) – это суждение общее по количеству (характеру субъекта) и утвердительное по качеству (характеру связи), т.е. суждение по логической форме: «Все S есть Р». Например: «Все адвокаты - юристы», «Каждый студент нашей группы получает стипендию».
Общеотрицательное суждение (Е) – общее по количеству и отрицательное по качеству, т.е. суждение по форме: «Ни одно S не есть Р». Например: «Ни один студент нашей группы не получает стипендию».
Частноутвердительное суждение (J) – частное по количеству и утвердительное по качеству, т.е. суждение по форме: «Некоторые S есть Р». Например: «Некоторые студенты нашей группы получают стипендию».
Частноотрицательноесуждение (О) – частное по количеству, отрицательное по качеству, т.е. по форме: «Некоторые S не есть Р». Например: «Некоторые студенты нашей группы не получают стипендию».
Чтобы в практике мышления правильно оперировать суждениями, необходимо знать распределенность в них терминов – субъекта и предиката. Распределенным считается термин, взятый в полном объеме, нераспределенным – если он мыслится не в полном объеме, а частично. Полный объем понятия означает, что данное понятие полностью включается или полностью исключается из объема другого понятия.
В общеутвердительных суждениях (А): «Все S есть Р» субъект распределен, а предикат не распределен. В общеутвердительных суждениях субъект в полном объеме включается в предикат. Это означает, что общеутвердительное суждение дает информацию обо все объеме субъекта, но лишь о части объема предиката. Поэтому субъект (как понятие) распределен, а предикат нераспределен.
В общеотрицательных суждениях (Е): «Ни одно S не есть Р» - субъект и предикат распределены, поскольку каждый из терминов исключен из другого. Иными словами, суждение дает информацию обо всем объеме субъекта и обо всем объеме предиката, поэтому оба термина распределены.
В частноутвердительном суждении (J): «НекоторыеSестьР» - субъект и предикат не распределены. Субъект и предикат такого суждения только частично включаются один в другой. Суждение дает информацию лишь о части объемов своих субъекта и предиката, т.е. они оба не распределены.
В частноотрицательномсуждении (О): «НекоторыеSне естьР» - субъект нераспределен, а предикат – распределен. В таком суждении предикат в полном объеме исключен из той части объема субъекта, о которой идет речь. На этом основании предикат в частноотрицательном суждении считается распределенным, а субъект нераспределенным.
Итак: субъект распределен (берется в полном объеме) в общих суждениях, в предикат распределен в отрицательных.
3. сложные суждения: логическая структура и виды
Сложные суждения – это суждения, образованные их простых посредством той или иной логической связи. Структура сложных суждений отличается от структуры простых суждений.Основными структурообразующими элементамиздесь выступают не понятия (термины – субъект и предикат), а самостоятельныепростые суждения, внутренняя субъектно-предикатная структура которых уже не учитывается. Связь между элементами сложного суждения осуществляется с помощью логических союзов: «и», «или»; «если...то...»; «если и только если..., то»; «неверно, что...», которые близки к соответствующим грамматическим союзам, но полностью с ними не совпадают. Главное их отличие состоит в том, что логические союзы однозначны, тогда как грамматические союзы имеют множество смыслов и оттенков.
Эти типы связи простых суждений выражаются соответствующими логическими связками: конъюнкцией («и»), дизъюнкцией («или»), строгой дизъюнкцией(«либо, ...либо»), импликацией («если..., то»), эквиваленцией(тогда и только тогда, когда...», отрицанием («неверно, что...»). Логические связки обозначают символами: 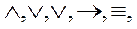 ~ соответственно. Каждый из этих логических союзов, за исключением отрицания, является бинарным, т.е. соединяет только два суждения, независимо от того простые они или сами, в свою очередь, сложные, имеющие внутри себя собственные союзы.
~ соответственно. Каждый из этих логических союзов, за исключением отрицания, является бинарным, т.е. соединяет только два суждения, независимо от того простые они или сами, в свою очередь, сложные, имеющие внутри себя собственные союзы.
Сложные суждения рассматриваются в логике только с точки зрения их истинностных значений, которые зависят от истинностных значений простых суждений, входящих в него, а также от характера связи этих суждений. Характер связи определяется смыслом логических союзов, который состоит в ответе на вопрос: при каких условиях сложное суждение будет истинно, а при каких – ложно. Иначе говоря, при каких сочетаниях истинности и ложности простых суждений, входящих в сложное, данный логический союз дает истинную связь, а при каких - ложную. Смысл логических союзовможно определить с помощью, так называемой истинностной таблицы, в которой на входе (см. Табл.1, столбцы 1,2) выписываются все возможные комбинации истинностных значений простых суждений (входящих в рассматриваемое сложное), а на выходе (Таблица 1 – столбцы 3 – 9) – значения сложного суждения, образованного из данных простых с помощью соответствующего логического союза.При этом, исходные простые суждения обозначают буквами: А,В,С,D..., а значения истинности символами: «и» - истино; «л» - ложно.
Таблица 1.
| NN | |||||||||
| А | В | А 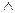 В В | А 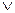 В В | А 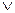 В В | А 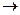 В В | А 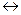 В В | ~А | ~В | |
| 1. | и | и | и | и | л | и | и | л | л |
| 2. | и | л | л | и | и | л | л | л | и |
| 3. | л | и | л | и | и | и | л | и | л |
| 4. | л | л | л | л | л | и | и | и | и |
Виды сложных суждений
По характеру логической связи выделяют пять основных видов сложных суждений: соединительные (конъюнктивные), разделительные (дизъюнктивные), условные (импликативные), эквивалентные, отрицаемые.
Соединительное или конъюнктивное суждение – это сложное суждение, образованное из исходных суждений посредством логического союза «и», обозначаемого символом « 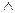 ». Например, суждение: «Сегодня я пойду на лекцию по логике и в кино» является конъюнктивным суждением, состоящим из двух простых суждений (обозначим их соответственно – А, В): : «Сегодня я пойду на лекцию по логике» (А), «Сегодня я пойду в кино» (В). Символически данное сложное суждение можно записать как: А
». Например, суждение: «Сегодня я пойду на лекцию по логике и в кино» является конъюнктивным суждением, состоящим из двух простых суждений (обозначим их соответственно – А, В): : «Сегодня я пойду на лекцию по логике» (А), «Сегодня я пойду в кино» (В). Символически данное сложное суждение можно записать как: А 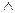 В, где А,В – элементы конъюнкции; «
В, где А,В – элементы конъюнкции; « 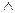 » - символ логического союза – конъюнкции. В русском языке конъюнктивный логический союз выражается многими грамматическими союзами: и, а, но, да, хотя, однако, а также... Нередко подобные грамматические союзы заменяются запятой, двоеточием, точкой с запятой. Например, в суждении «Русские долго запрягают, да быстро ездят».
» - символ логического союза – конъюнкции. В русском языке конъюнктивный логический союз выражается многими грамматическими союзами: и, а, но, да, хотя, однако, а также... Нередко подобные грамматические союзы заменяются запятой, двоеточием, точкой с запятой. Например, в суждении «Русские долго запрягают, да быстро ездят».
Конъюнктивное суждение истинно только при истинности всех составляющих его элементови ложно при ложности хотя бы одного из них (см. табл.1 – столбец 3).
Знание особенностей истинностного значения конъюнкции имеет особое значение в практике мышления, т.к. достаточно одного ложного суждения, чтобы придать всей, даже весьма сложной, конъюнктивной мысли ложность. Этот факт лежит в основе многих русских пословиц, например, о том, что делает ложка дегтя в бочке меда. Эту особенность важно учитывать в юридической практике, в дискуссиях – когда выстраивается сложная цепь мыслей, которая при одном ложном звене может распасться. С другой стороны, достаточно обнаружить хотя бы один ложный аргумент в доводах оппонента, чтобы опровергнуть все его рассуждение в целом.
Разделительноеилидизъюнктивное суждение – это сложное суждение, образованное из исходных суждений посредством логического союза «или», обозначаемого символом « 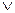 ». Например, суждение: «Право может способствовать экономическому развитию или препятствовать ему» является дизъюнктивным суждением, состоящим из двух простых: «Право может способствовать экономическому развитию», «Право может препятствовать экономическому развитию». Соответственно обозначив их через буквы А, В – выделим его логическую форму: А
». Например, суждение: «Право может способствовать экономическому развитию или препятствовать ему» является дизъюнктивным суждением, состоящим из двух простых: «Право может способствовать экономическому развитию», «Право может препятствовать экономическому развитию». Соответственно обозначив их через буквы А, В – выделим его логическую форму: А 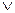 В.
В.
Поскольку связка «или» употребляется в двух разных значениях – неисключающем и исключающем, то различают слабуюисильную дизъюнкции соответственно. Выше приведенный пример является слабой дизъюнкцией, т.к. право одновременно в одном отношении может способствовать развитию экономики, но препятствовать в другом. Слабая дизъюнкция является истинной в тех случаях, когда истинно по крайней мере одно из составляющих ее суждений (или оба вместе) и ложна, когда оба составляющих ее суждения ложны (Табл.1 – столбец 4).
Сильная дизъюнкция (символ « 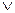 ») отличается от слабой тем, что ее составляющие исключают друг друга. Например: «Преступление может быть умышленным или по неосторожности». Для того, чтобы подчеркнуть строго разделительный, исключающий характер связи, в естественном языке используется усиленная двойная форма разделения: «...либо...либо», «или...или», например: «Либо я найду путь, либо я проложу его». Строгая дизъюнкция истинна лишь тогда, когда одно из составляющих ее суждений истинно, а другое – ложно (Табл. 1 – столбец 5).
») отличается от слабой тем, что ее составляющие исключают друг друга. Например: «Преступление может быть умышленным или по неосторожности». Для того, чтобы подчеркнуть строго разделительный, исключающий характер связи, в естественном языке используется усиленная двойная форма разделения: «...либо...либо», «или...или», например: «Либо я найду путь, либо я проложу его». Строгая дизъюнкция истинна лишь тогда, когда одно из составляющих ее суждений истинно, а другое – ложно (Табл. 1 – столбец 5).
Среди дизъюнктивных суждений следует различать также полнуюинеполную дизъюнкцию, когда соответственно: перечислены все признаки, виды определенного рода или это перечисление остаетсяоткрытым (неполным), что в естественном языке выражается словами: «и т.д.», «и др.».
Дизъюнктивные суждения широко распространены в практике мышления. Именно в них выражается логическая операция деления.
Условноеилиимпликативное суждение – это сложное суждение, в котором суждения объединяются логическим союзом «если..., то» (символ « 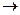 »), например: «Если правительство нарушает закон, то порождает неуважение к нему», «Если число делится на 2 без остатка, то оно четное». Условное суждение состоит из двух составляющих его суждений. Суждение, выраженное после слова «если» называется основанием или антецедентом (предыдущим), а суждение – после слова «то» называется следствием или консеквентом (последующим). Формула условного суждения: А
»), например: «Если правительство нарушает закон, то порождает неуважение к нему», «Если число делится на 2 без остатка, то оно четное». Условное суждение состоит из двух составляющих его суждений. Суждение, выраженное после слова «если» называется основанием или антецедентом (предыдущим), а суждение – после слова «то» называется следствием или консеквентом (последующим). Формула условного суждения: А 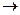 В, где А – основание, В – следствие. При этом, суждения, выполняющие роль основания и следствия, сами по себе могут быть как простыми, так и сложными суждениями.
В, где А – основание, В – следствие. При этом, суждения, выполняющие роль основания и следствия, сами по себе могут быть как простыми, так и сложными суждениями.
Образуя условное суждение, прежде всего, имеют в виду, что не может быть так, чтобы то, о чем говорится в основании имело место, а то, о чем говорится в следствии отсутствовало. Иными словами, не может случится, чтобы антецедент был истинным, а консеквент – ложным. Это и определяет то, что условное суждение истинно во всех случаях, кроме одного: когда предшествующее есть, а последующего нет (т.е. – суждение по форме А 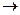 В – ложно только в одном случае, когда А – истинно, а В – ложно). Это выражено в таблице 1 – столбец 6.
В – ложно только в одном случае, когда А – истинно, а В – ложно). Это выражено в таблице 1 – столбец 6.
В форме условных суждений выражают как объективные зависимости одних объектов от других, так и права и обязанности людей, связанные с теми или иными условиями.
Эквивалентное суждение – это сложное суждение, в котором объединяются суждения с взаимной условной зависимостью. Поэтому они также называются двойной импликацией. Они образуются с помощью логического союза «если и только если..., то», который обозначается символом « 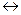 ». Формула эквивалентности: А
». Формула эквивалентности: А 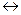 В,гдеА, В – суждения, из которых образуется эквивалентное суждение, например: «Человек имеет право на пенсию по возрасту, если и только если он достиг пенсионного возраста». В естественном языке, в том числе в экономических и юридических текстах, для выражения эквивалентных суждений используются грамматические союзы: «лишь при условии, что..., то», «только тогда, когда..., то», «в том и только в том случае, когда..., тогда».
В,гдеА, В – суждения, из которых образуется эквивалентное суждение, например: «Человек имеет право на пенсию по возрасту, если и только если он достиг пенсионного возраста». В естественном языке, в том числе в экономических и юридических текстах, для выражения эквивалентных суждений используются грамматические союзы: «лишь при условии, что..., то», «только тогда, когда..., то», «в том и только в том случае, когда..., тогда».
Условия истинности эквивалентных суждений представлены в 7-ом столбце таблицы 1: эквивалентное суждение истинно в двух случаях – когда оба составляющих его суждения истинны или когда оба ложны. Иными словами, связь (отношение) между элементами эквивалентного суждения можно охарактеризовать как необходимую: истинность А достаточна для признания истинности В и наоборот; ложность А служит показателем ложности В и наоборот.
Отрицаемое суждение – это сложное суждение, образованное с помощью логического союза «неверно, что...» (или просто «не»), который именуется знаком отрицания (символ «~»). В отличие от вышеотмеченных бинарных союзов он относится к одному суждению. Прибавление его к какому-либо суждению означает образование нового суждения, которое находится в определенной зависимости от исходного: отрицаемое суждение истинно, если исходное ложно, и наоборот. Это выражено в таблице1 – столбцы 8,9. Например, если исходное суждение: «Все свидетели правдивы», то отрицаемое: «Неверно, что все свидетели правдивы».
Все выделенные виды сложных суждений используются в обычных рассуждениях и контекстах, в том числе экономических и правовых. Для более точного уяснения смысла этих контекстов важно овладение навыками логического анализа сложных суждений с использованием символического языка для выражения их логической структуры. Часто для достижения определенности высказывания необходимо выявить главную связь в суждении. Например, высказывание «Преступление совершено А и В или С» не отличается определенностью, поскольку не ясно, какая из двух логических связок – конъюнкция или дизъюнкция – является главной. Поэтому данное высказывание может быть истолковано как конъюнктивное суждение (1): «А и (В или С)», а может и как дизъюнктивное суждение (2): «(А и В) или С». Но по логической значимости, т.е. по их истинностному значению, они не эквиваленты. Это можно определить, построив для них истинностные таблицы, и по ним сравнить истинностные значения этих суждений.
С этой целью важно знать, как вообще строятся истинностные таблицы для различных сложных суждений. Осуществляется это следующим образом.
На входе таблицы:
1. Выписывают все простые суждения (А, В, С, D...), входящие в рассматриваемое сложное суждение. Пусть их число будет n.
2. Определяют число к строк в таблице по формуле к = 2n
3. В столбцах входа таблицы выписывают все возможные комбинации истинностных значений простых суждений в следующем порядке: в самом правом столбце чередуют и и л по одному; во втором справа столбце чередуют подряд два значения и и два значения л; в третьем столбце чередуют подряд четыре значения и и четыре значения л; в четвертом столбце – восемь значений и подряд и восемь значений л подряд и т.д.
На выходе таблицы:
4. Слева направо выписывают логические формы всех сложных суждений, входящих в рассматриваемое суждение, по порядку: в начале суждения 1-ой степени сложности (т.е. с одним логическим знаком); затем 2-ой степени (с двумя логическими союзами); далее 3-ей степени (с тремя логическими союзами) и так до тех пор, пока последнее суждение не будет представлять логическую форму исходного сложного суждения.
5. Столбцы истинностных значений для выписанных логических форм образуют исходя из: (1) смысла логического союза (см. таблицу 1) и (2) значений истинности, которые принимают простые суждения, входящие в данную форму (см. строки входа таблицы).
Мы можем сравнить вышеотмеченные суждения (1) и (2). С этой целью теперь построим таблицу 2 для конъюнктивного суждения (1), выразив его символически как «А 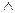 (В
(В 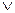 С)», и таблицу 3 для дизъюнктивного суждения (2), записав его символически как «(А
С)», и таблицу 3 для дизъюнктивного суждения (2), записав его символически как «(А 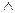 В)
В) 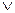 С».
С».
| Таблица 2 | Таблица 3 | |||||||||
| А | В | С | В 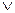 С С | А 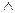 (В (В 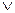 С) С) | А | В | С | А 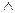 В В | (А 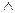 В) В) 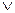 С С | |
| и | и | и | и | и | и | и | и | и | и | |
| и | и | л | и | и | и | и | л | и | и | |
| и | л | и | и | и | и | л | и | л | и | |
| и | л | л | л | л | и | л | л | л | л | |
| л | и | и | и | л | л | и | и | л | и | |
| л | и | л | и | л | л | и | л | л | л | |
| А | В | С | В 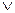 С С | А 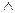 (В (В 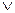 С) С) | А | В | С | А 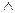 В В | (А 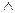 В) В) 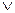 С С | |
| л | л | и | и | л | л | л | и | л | и | |
| л | л | л | л | л | л | л | л | л | л |
Из таблиц 2 и 3 видно, что истинностные значения суждений (1) и (2) не одинаковы (в двух строках – когда одно ложно, другое истинно), и следовательно они не эквивалентны, и представляют суждения, выражающие различные связи между их структурными элементами.
Таким образом, для осуществления логического анализа формы сложных суждений необходимо записать их символически в виде формулы и построить соответствующие истинностные таблицы с последующим их сравнением.
