Непараметрические критерии различия

Вычисление среднейарифметической величины

В простейшем случае этот показатель вычисляется путем сложения всех полученных значений (которые называются вариантами) и деления суммы на число вариант:

где ∑—знак суммирования;V — полученные в исследовании значения (варианты); п —число вариант.

По этой формуле вычисляется так называемая простая средняя арифметическа явеличина .

При большом числе вариант прибегают к вычислению так называемой взвешенной среднейарифметической величины. С этой целью строят ряд распределения, или вариационный ряд, который представляет собой ряд вариант и их частот, характеризующих какой-нибудь признак в убывающем или возрастающем порядке.

Вычисление средней ошибки среднего арифметического

Условное обозначение средней ошибки среднего арифметического — т. Следует помнить, что под «ошибкой» в статистике понимается не ошибка исследования, а мера

представительства данной величины, т. е. мера, которой средняя арифметическая величина, полученная на выборочной совокупности, отличается от истинной средней арифметической величины, которая была бы получена на генеральной совокупности. Вычисление средней ошибки среднего арифметического, которое производится по формуле:

Вычисление средней ошибки Разности

Условное обозначение средней ошибки разности —t

Формулы определения достоверности разности представлены следующим образом:

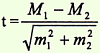для средних величин

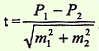для относительных показателей

где t - критерий достоверности, m1 и m2 - ошибки репрезентативности, М1 и М2 - средние величины, Р1 и Р2 - относительные показатели.

Если вычисленный критерий t более или равен 2 (t ≥ 2), то разность следует считать достоверной (существенной), т.е. обусловленной влиянием какого-то фактора, что будет иметь место и в генеральной совокупности.

При t < 2, это означает, что разность недостоверна, случайна, т.е. не обусловлена какой-то закономерностью (не обусловлена влиянием какого-то фактора).

Непараметрические критерии различия

непараметрических критериев различияприменяют когда нужно рассчитать достоверность различий между небольшими совокупностями показателей, которые или имеют порядковый или не подчиняются закону нормального распределения

Наибольшей статистической мощностью отличаются параметрические критерии.

непараметрических критериев различияне нуждаются в вычислении параметров, характеризующих те или иные выборки (среднего арифметического, среднего квадратического и т. п.).

Существует несколько непараметрических критериев,в зависимости от конструкции и статистической мощности. Наиболее распространенными являются критерий Уайта и критерий Вилкоксона.

Критерий Уайта. Условное обозначение этого критерия— Т. Он способен выявить различия между двумя совокупностями по их ведущим тенденциям, однако не

оценивая степени колебания вариант. Критерий Уайта применим при сравнении одинаковых и разных по объему выборок.

Критерий Вликоксона. Условное обозначение этого критерия — Z. Он применяется в тех случаях, когда необходимо сравнить различия между парными вариантами, составляющими две выборки. Парных вариант должно быть не менее 6.

Таблицы и рисунки

Основные правила составления таблиц:

1. Нумерация таблиц делается сквозной арабскими цифрами. Слово «Таблица» (сокращать нельзя) и порядковая цифра (без знака №) пишутся в правом верхнем углу над текстовым заголовком.

2. Текстовые заголовки таблиц размещают посередине строки над таблицей с прописной буквы без точки на конце.

3. Таблица не должна быть «вытянутой» по вертикалиили занимать небольшую часть по ширине страницы.

4. Однотипные таблицы необходимо строить одинаково.

5. Нумерация колонок и граф оправдывается только в тех случаях, когда в последующем изложении необходимо будет делать на нее ссылки.

6. Колонка «Примечания» вводится в том случае, когда ее содержание относится к большинству граф таблицы. В остальных случаях примечания помещают под таблицей в отдельной строке или в сноске.

7. Рекомендуется избегать вертикальных надписей в «головке» таблицы.

8.Нецелесообразно применять диагональные линии в «головке» боковика таблицы.

9. Каждая часть таблицы должна иметь свой заголовок. Нельзя оставлять пустыми графы и колонки.

10. Каждый заголовок должен быть по возможности кратким.

11. Числовые данные таблицыне должны сопровождаться размерностями.

12. Когда в полученных результатах имеется постоянное числовое значение показателя для нескольких изменяющихся величин, его не повторяют, а выносят в текстовой заголовок.

13. Числовые значения в таблице не должны сопровождаться словами «примерно», «не менее», «не более» «менее», «более», а пределы положительных чисел — предлогами «от» и «до».

14. Числовые показатели должны иметь одинаковое число знаков после запятой, а классы чисел располагаются один под другим.

15. В текстовых таблицах начальные слова, размещенные в графах и колонках, пишутся с прописной буквы. В конце точка не ставится.

Рисунки

Иллюстрации любого содержания и графического исполнения называют рисунками

Любые рисунки должны включать все необходимые обозначения, чтобы быть понятными и давать отчетливое представление о наиболее важных чертах изученного явления. Все второстепенные части рисунка призваны способствовать выявлению смысла целого. Поэтому рекомендуется максимально освобождать рисунок от лишних линий и надписей, оставляя только те, которые абсолютно необходимы для понимания рисунка.

Выбор исследуемых.

Выбор исследуемых можно проводить следующими способами:

1.типологическим отбором.( Уравнивание характеристик исследуемых лиц по возрасту, полу, физической подготовленности, профессиональной принадлежности и т. п.)

2 выборочный метод(изучаются не все единицы той или иной совокуп-

ности, а лишь отобранная их часть.)

3.способ случайной выборки(способом алфавитных списков, способ лотереи, использование таблиц случайных чисел)