Краткие методические указания к решению задачи 4
Графики Лоренца получили широкое распространение при изучении степени неравномерности распределения (неравномерности концентрации) различных суммарных показателей в группах единиц наблюдения, образованных в зависимости от численных значений этих же показателей или других, тесно взаимосвязанных с ними показателей. Например, распределение совокупного денежного дохода по группам населения в зависимости от размеров получаемых денежных доходов, или распределение продовольственных фондов по группам населения в зависимости от размеров получаемых денежных фондов и т.д.
Применение графиков Лоренца во времени или по разным объектам позволяет рассматривать их как многоплановый и эффективный инструмент статистического анализа, взаимосвязанный с традиционными методами статистики и расширяющий сферы их применения.
Если обозначить согласно общепринятой символики в статистике частотное распределение единиц наблюдения по признаку 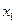 через «
через « 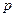 », а распределение совокупного признака
», а распределение совокупного признака 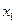 по этим же группам через «
по этим же группам через « 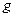 », совокупного признака
», совокупного признака 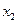 через «
через « 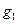 » и т. д., то, согласно условию задачи, следует последовательно сопоставить следующие пары частотных распределений: 1) «
» и т. д., то, согласно условию задачи, следует последовательно сопоставить следующие пары частотных распределений: 1) « 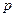 » и «
» и « 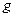 »; 2) «
»; 2) « 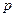 » и «
» и « 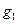 »; 3) «
»; 3) « 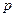 » и «
» и « 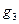 »; Построить соответствующие графики.
»; Построить соответствующие графики.
Важно подчеркнуть, что в целях упрощения расчетов и повышения аналитичности данных, единицы наблюдения, как правило, распределяются на равные группы: 10 групп и 10% единиц наблюдения в каждой группе, 5 групп по 20% единиц наблюдения и т. д. Это учтено при определении числа групп в табл. 12 задачи 2.
Последовательность решения задачи следующая:
Во-первых, для каждой пары сопоставляемых распределений рассчитывают кумулятивные (накопленные) частоты.
Во-вторых, на осях ординат строится квадрат 100х100, который делится пополам диагональной прямой линией – линией равномерного распределения. На ось абсцисс наносят кумулятивные итоги «Cum p», а на ось ординат – кумулятивные итоги «Cum g». По значениям каждой пары кумулятивных итогов строится кривая Лоренца.
В-третьих, рассчитывается коэффициент Джини:
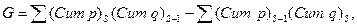
где 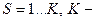 число групп.
число групп.
Чем ближе коэффициент Джини к единице, тем больше степень концентрации или степень неравномерности распределения. Если в расчетах используются проценты, то результат вычисления коэффициента Джини следует разделить на 10000 (100  100).
100).
Ниже для иллюстрации в табл. 17 представлены результаты решения задачи с равномерными интервалами распределения 10% единиц наблюдения по 10 группам, полученные по данным базового варианта.
Таблица 17
Сопоставление распределения « 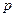 » и «
» и « 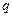 », %
», %
| Номер группы | « 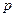 » » | « 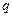 » » | « 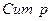 » » | « 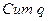 » » |
| 5,29 | 5,29 | |||
| 6,72 | 12,01 | |||
| 7,88 | 19,89 | |||
| 9,04 | 28,93 | |||
| 9,47 | 38,40 | |||
| 10,71 | 49,11 | |||
| 11,47 | 60,58 | |||
| 11,78 | 72,37 | |||
| 12,58 | 84,99 | |||
| 15,05 | 100,00 | |||
| Итого | - | - |
По данным табл.17 строится кривая Лоренца:
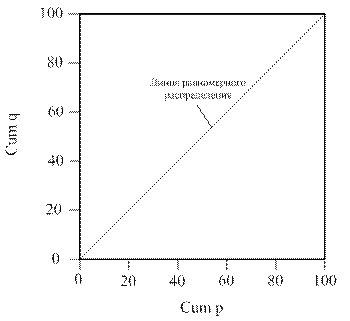
Рис.1 Кривая Лоренца
Рассчитаем коэффициент Джини:
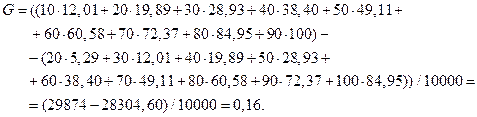
Аналогичная процедура повторяется для распределения « 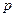 » и «
» и « 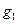 »; и «
»; и « 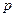 » и «
» и « 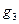 »;
»;
Ниже для иллюстрации в табл. 18 представлены результаты решения задачи с равномерными интервалами распределения 20% единиц наблюдения по 5 группам, полученные по данным базового варианта. Для ее заполнения используются данные табл. 2 задачи 2.
Таблица 18
Сопоставление распределения « 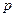 » и «
» и « 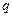 », %
», %
| Номер группы | « 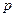 » » | « 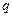 » » | « 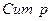 » » | « 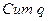 » » |
| 12,78 | 12,78 | |||
| 16,77 | 29,55 | |||
| 20,00 | 49,55 | |||
| 23,06 | 72,61 | |||
| 27,38 | ||||
| Итого | - | - |
По данным табл.18 строится кривая Лоренца и коэффициент Джини:
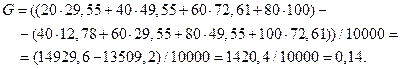
Аналогичная процедура повторяется для распределения « 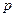 » и «
» и « 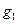 »; и «
»; и « 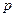 » и «
» и « 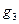 »;
»;
Задача 5
По исходным данным провести вторичную группировку по признаку 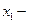 денежным доходам семьи за месяц, образовав группы с равными интервалами: 3000-4500; 4500-6000; 6000-7500; 7500-9000; 9000-10500; 10500-12000.
денежным доходам семьи за месяц, образовав группы с равными интервалами: 3000-4500; 4500-6000; 6000-7500; 7500-9000; 9000-10500; 10500-12000.
