Треугольником и звездой

Если при смешанном соединении резистивных элементов не удается определить эквивалентное резистивное сопротивление, то необходимо эквивалентное преобразование таких цепей. Примером упрощения расчетов служит преобразования мостовой схемы соединения резистивных элементов (рис. 1.16).

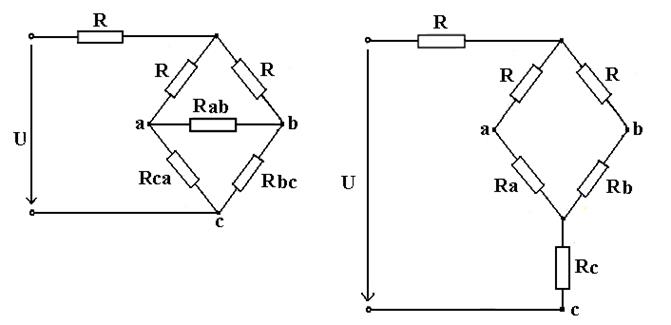
Рис.1.16. Преобразование мостовой схемы в эквивалентную схему, соединённую звездой и треугольником

После замены треугольника abc с резисторами 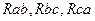эквивалентной звездой abc с резисторами 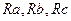, всю цепь можно рассматривать как смешанное соединение резисторов.

Для преобразования треугольника в эквивалентную звезду, найдем сопротивление между узлами a и b.

Для схемы треугольника проводимость между узлами a и b определим из соотношения:

.

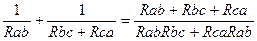Тогда сопротивление между узлами a и b будет:

/( ).

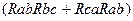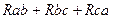Для схемы звезды сопротивление между узлами a и b равно: .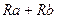

Согласно условию эквивалентности можно записать равенство:

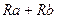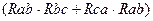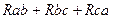= /( ). (1.37)

Аналогично, путем циклической перестановки индексов, можно получить уравнения равенства сопротивлений между узлами b и c, c и a:

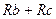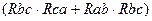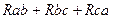= /( ), (1.38)

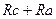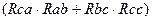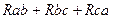= /( ). (1.39)

Для определения сопротивления 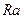звезды сложим (1.37) и (1.39), вычтем (1.38) и, разделив полученное выражение на 2, найдем

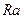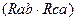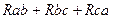= /( ). (1.40)

Путем циклической перестановки найдем сопротивления 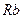и :

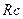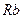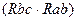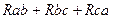= /( ) (1.41)

Rc = 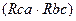/( 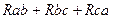). (1.42)

В случае равенства сопротивлений ветвей треугольника, сопротивления ветвей эквивалентной звезды тоже одинаковы и определяются по формуле:

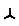R = R∆ / 3. (1.43)

При обратном преобразовании звезды в эквивалентный треугольник перемножим попарно (1.40) и (1.451), (1.41) и (1.42), (1.42) и (1.40) и сложим полученные произведения:

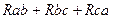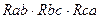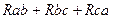= ( ) / ( ). (1.44)

Выражение (1.44) разделим на (1.42) и определим сопротивление 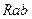ветви треугольника:

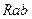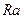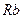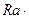
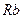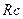= + +( ) / . (1.45)

Путем циклической перестановки найдем сопротивления 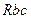и 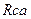других ветвей треугольника:

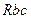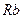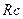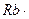
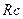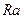= + + ( ) / ; (1.46)

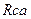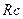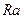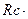
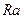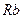= + +( ) / . (1.47)

При равенстве сопротивлений ветвей звезды, сопротивления ветвей эквивалентного треугoльника тоже одинаковы и определяются по формуле:

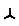R∆ =3R. (1.48)

1.6. Работа и мощность постоянного тока. Закон Джоуля – Ленца

Источник электрической энергии совершает полезную работу в замкнутой электрической цепи, при этом возникает электрический ток. Работа источника связана с перемещением электрического заряда Q и зависит от ЭДС:

A = E∙Q. (1.49)

Так как Q = I∙ t, E = U+UBT, то A = (U+UBT)I∙t или A = U∙I∙t + UBТ ∙I∙t,

где U∙I∙t = А - работа, совершаемая источником на внешнем участке цепи,

UBТ ∙I∙t = АBT - потери энергии внутри источника.

Используя закон Ома для участка цепи, можно записать:

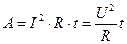. (1.50)

Мощностью источника постоянного тока называют работу источника, совершаемую за единицу времени:

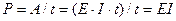. (1.51)

Мощность потребителей:

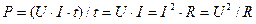. (1.52)

Мощность потерь энергии внутри источника:

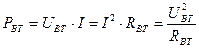. (1.53)

Единица мощности - ватт (Вт):

.

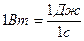Единица электрической работы - джоуль (Дж):

.

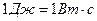На практике пользуются единицей мощности киловатт (кВт): 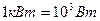и единицей работы (киловатт-час): .

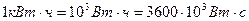При прохождении тока по проводнику свободные электроны, перемещаясь под действием поля, сталкиваются с ионами кристаллической решетки проводника. При этом кинетическая энергия электронов передается ионам, увеличивая при этом их амплитуду колебания, что приводит к нагреванию проводника. Количество теплоты, выделяемой в проводнике при прохождении тока, пропорционально квадрату силы тока, сопротивлению проводника и времени прохождения тока, и носит название закона Джоуля - Ленца:

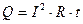(Дж). (1.54)

Преобразование электрической энергии в тепловую энергию имеет большое практическое значение и широко используется в нагревательных приборах, в устройствах электрического освещения. Однако часто тепловые потери являются нежелательными, например, в электрических машинах, трансформаторах и других устройствах, что снижает их КПД. Во избежание перегрева проводов, обмоток электрических машин, электрических аппаратов установлены нормы допустимого значения силы тока и сечений проводников, которые приводятся в Правилах устройства электрических установок.

Например, необходимо рассчитать сечение провода на допустимый ток. Если расстояние между источником электрической энергии и потребителем 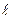(м), то длина двух проводов - 2 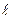(м). Сопротивление проводов сечением S (м²) с удельным сопротивлением 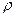(Ом · м) равно: 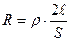. Падение напряжения на проводах 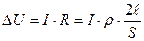, тогда сечение проводов 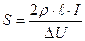. Найденное сечение проводов округляют до большего стандартного ближайшего значения.

Для защиты электрических аппаратов, машин и приборов от больших токов используются предохранители и автоматы.

При расчете параметров электрических цепей необходимо соблюдать баланс мощностей: алгебраическая сумма мощностей всех источников энергии электрической цепи равна арифметической сумме мощностей всех приемников энергии:

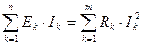. (1.55)

Есл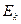и и 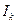совпадают по направлению, то мощности источников электрической энергии положительны. При несовпадении направлени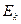й и 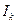- мощности источников электрической энергии отрицательны.