Определение 1. Пусть и произвольные множества. Соответствием называется тройка множеств 6 страница

0 2 0 2

Рис. 5.7. Области истинности для Рис. 5.8. Области истинности

функций y₂, y₇, y₈, y₉ для функций y₃, y₁₀, y₁₄

На рис. 5.7 и 5.8 пунктирной линией показаны границы областей истинности для конъюнкции, сложения по модулю 2, дизъюнкции, стрелки Пирса, импликации , эквиваленции и запрета (сравните выделенные области с соответствующими строками , , , , , , нашей таблицы).

Собственно бинарных функций в табл. 1 только десять, т.к. и логические константы (0 и 1), а , , и - унарные функции, т.е. функции одной переменной, из которых практический интерес представляет лишь одна унарная булева функция , называемая инверсией (отрицанием) переменной.

Итак, в качестве простейших булевых функций мы получили две логические константы, одну унарную и десять бинарных функций. Ниже покажем, что изначальных булевых функций, из которых строятся все остальные, гораздо меньше.

Вопросы для самоконтроля

1. По табл. 5.1 определите области истинности для функций и .

2. Область истинности какой функции равна объединению областей истинности конъюнкции и сложения по модулю два?

3. Область истинности какой функции равна пересечению областей истинности эквиваленции и дизъюнкции?

5.2.2. Булевы формулы

Полученные выше логические операции соединения можно выразить через три основные булевы функции: инверсию, конъюнкцию и дизъюнкцию, т.е. через те логические операции, которыми мы уже давно пользуемся при составлении сложных условий. Из табл. 5.1 следуют правила отрицания (инверсии), логического умножения (конъюнкции) и логического сложения (дизъюнкции), которые можно представить отдельной таблицей.

Таблица 5.2

Подставляя в конъюнкции вместо переменной ее инверсию (осуществляя композицию конъюнкции и инверсии), получим новую булеву функцию . Согласно табл. 5.2 областью истинности данной функции будет множество . Только на вершине эта функция имеет значение единицы, а на всех остальных вершинах единичного квадрата она обращается в нуль. Но ту же область истинности имеет и запрет , т.е. данные функции одно и то же. Поэтому

= = . (5.19)

Иначе говоря, мы выразили функцию через конъюнкцию и дизъюнкцию формулой (5.19). Аналогично можно выразить и другие булевы функции, область истинности которых содержит только одну вершину единичного квадрата. Получим

= = , (5.20)

= = . (5.21)

Замечание 1. Из полученных результатов следует очень простое правило получения формул, использующих операции инверсии и конъюнкции, для аналитического выражения булевых функций с областью истинности из одной вершины единичного квадрата. Формула эта строится по координатам той самой вершины:– единица заменяется соответствующей переменной, а нуль ее инверсией, и берется их конъюнкция.

5.2.3. Совершенные дизъюнктивные нормальные формы

Распространим полученные результаты предыдущего параграфа на 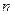-арные булевы функции. Функция выделяет на гиперкубе некоторое подмножество вершин – область истинности этой функции.

Если эта область содержит только одну вершину , то согласно установленному выше правилу (замечание 1, п. 5.2.2) формулу данной функции можно построить по координатам данной вершины. Такая формула будет представлять конъюнкцию булевых величин вида

(5.22)

Такие формулы называются элементарными конъюнкциями длины .

Определение 21. Элементарная конъюнкция называется полной, если она является формулой для булевой функции (имеющей область истинности из одной только вершины гиперкуба). Длина полной элементарной конъюнкции всегда равна размерности гиперкуба. Если длина элементарной конъюнкции меньше , то она называется неполной.

Пусть теперь некоторая функция имеет область истинности, которая состоит из 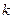вершин гиперкуба . Координаты этих вершин можно записать в матрице с числом строк 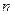и числом столбцов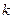

Такую матрицу называют булевой. Каждый из ее столбцов определяет координаты одной из вершин области истинности булевой функции . Тогда для данной функции можно построить следующую формулу:

(5.23)

Определение 22. Формула (5.23) называется совершенной дизъюнктивной нормальной формой (СДНФ) булевой функции . Она представляет собой дизъюнкцию всех полных конъюнкций для всех вершин области истинности этой функции.

Очевидно, полная конъюнкция является частным случаем совершенной ДНФ* (подобно тому, как столбец является частным случаем матрицы). Поэтому можно утверждать, что формулу (5.23) можно построить для любой булевой функции, имеющей непустую область истинности. Иначе говоря, совершенная ДНФ существует для любой булевой функции, кроме константы «ложь». Однако эту константу можно определить более простой формулой , использующей только две из трех основных (теперь их так уже можно называть с полным правом!) логических операций.

Итак, основу мироздания булевых функций могут составлять всего лишь три простейшие логические операции – инверсия, конъюнкция и дизъюнкция. С помощью их различных композиций получаются любые другие булевы функции. Это означает, что система из данных трех логических операций является функционально полной системой булевых функций (см. далее).

Пример 5.9. Построить совершенную

ДНФ для булевой функции , 001 101

область истинности которой есть передняя

грань куба (рис. 5.9). 010 110

Решение. Передняя грань содержит 4

вершины, координаты которых запишем в 000 100

булевой матрице

Рис. 5.9. Графическая интерпретация СДНФ

,

которая, как показано выше, равна троичному вектору x0x, записанному здесь в виде вектор-столбца. Согласно (5.23) получим формулу

которая и будет ответом на поставленный вопрос.

Замечание 1. Для сокращения записи булевых формул допускается опускать символ дизъюнкции (подобно тому, как в элементарной алгебре опускается символ операции умножения).

Замечание 2. С помощью круглых скобок в алгебраических формулах задается порядок выполнения арифметических действий, а при отсутствии скобок порядок действий определяется согласно их приоритетам. Например, операция умножения имеет больший приоритет и выполняется раньше сложения. Так и конъюнкция (логическое умножение) имеет больший приоритет по отношению к дизъюнкции (логическому сложению). Потому в правой части равенства (5.23) круглые скобки можно опустить.

С учетом сделанных замечаний результат решения последнего примера может быть записан более компактно, а именно:

.

Будем придерживаться такой, более простой, формы записи булевых формул и дальше.

Пример 5.10. Найти совершенную ДНФ для булевой функции, областью истинности которой является первый слой куба (рис. 5.9).

Решение. Веса, равные единице, имеют следующие вершины данного куба: 001, 010, 100. Тогда по определению первым его слоем будет множество {001, 010, 100}. Составим для данной области булеву матрицу:

.

Первый столбец данной матрицы задает полную элементарную конъюнкцию – , второй – и третий – . Тогда искомая ДНФ будет .

Вопросы для самоконтроля

1. Определите совершенные ДНФ для двух функций, области истинности которых верхнее переднее и правое переднее ребра куба (рис. 5.8) соответственно. Затем получите ДНФ для функции с областью истинности, равной пересечению указанных выше ребер. Сравните полученные ДНФ.

2. Чему равна область истинности конъюнкции двух функций – объединению или пересечению их областей истинности?

3. Чему равна область истинности дизъюнкции двух функций – объединению или пересечению их областей истинности?

4. Что такое функционально полная система булевых функций?

5. Существуют ли такие булевы функции, которые нельзя выразить через дизъюнкцию, конъюнкцию и инверсию?

5.2.4. Булева алгебра

Данная алгебра, носителем которой является все множество булевых функций, а сигнатурой ) - три логические операции – инверсия, конъюнкция и дизъюнкция, восходит к трудам О. Де Моргана и Дж. Буля. Основные же тождества этой алгебры непосредственно следуют из табл. 5.1. Их можно использовать при алгебраических преобразованиях сложных булевых формул.

Пусть , и произвольные булевы функции. Тогда тождества булевой алгебры будут иметь следующий вид.

Свойства коммутативности операций :

1а. , 1б. .

Свойства ассоциативности операций :

2а. , 2б. .

Свойства дистрибутивности операций :

3а. ,

3б. .

Свойства нуля и единицы:

4а. - определение единицы,

4б. - определение нуля,

5а. , 5б. ,

6а. , 6б. ,

7а. , 7б. .

Свойства идемпотентности операций :

8а. , 8б. .

Законы поглощения:

9а. , 9б. .

Законы Де Моргана:

10а. , 10б. .

Сравнивая эти тождества с тождествами алгебры множеств, получаем полное их совпадение (с точностью до обозначения операций). Это совпадение объясняется тем, что любая булева функция по существу есть символ некоторого подмножества гиперкуба , которое является ее областью истинности. При этом дизъюнкция двух булевых функций будет означать операцию объединения их областей истинности, а конъюнкция – операцию пересечения этих областей. Универсумом в данном случае является гиперкуб . Булева функция, областью истинности которой является весь гиперкуб, - это константа «истина», т.е. 1. А булева функция, область истинности которой пустое множество, - это константа «ложь», т.е. 0. Дополнение области истинности функции на гиперкубе является областью ложности этой функции, т.е. областью истинности противоположной булевой функции . Поэтому операция инверсии равносильна операции дополнения над ее областью истинности.

Из данного сравнения следует, что булева алгебра и алгебра множеств суть одна и та же алгебра. В самом широком смысле алгебра называется булевой, если для нее выполняются тождества 1а – 10б независимо от природы элементов носителя и обозначения трех ее основных операций.

Рассмотрим несколько примеров на алгебраические преобразования булевых формул.

Пример 5.11. Упростить выражение ( ) ( ) ( ).

Решение. Используя тождества 1б, 2а и 3б, получим

(( ) ( )) ( ) ( ).