От грамматики к минимальному автомату

Утверждаю

Ректор университета

__________________А.В.Лагерев

«____»____________2005 г.

ТЕОРИЯ ВЫЧИСЛИТЕЛЬНЫХ ПРОЦЕССОВ

СИНТЕЗ КОМБИНАЦИОННОЙ СХЕМЫ

РАСПОЗНАЮЩЕГО КОНЕЧНОГО АВТОМАТА

Методические указания к выполнению

Расчетно-графической работы

Для студентов дневной формы обучения

специальности 230105 «Программное обеспечение вычислительной техники и автоматизированных систем»

Брянск 2005

УДК 004.4

Теория вычислительных процессов. Синтез комбинационной схемы распознающего конечного автомата: методические указания к выполнению расчетно-графической работы для студентов дневной формы обучения специальности 230105 «Программное обеспечение вычислительной техники и автоматизированных систем». - Брянск: БГТУ, 2005.- 29с.

Разработал:

А.Н. Горбунов

канд. техн. наук, доц.

Рекомендовано кафедрой «Информатика и программное обеспечение» БГТУ (протокол №3. от 18.10.05г.)

Научный редактор В.В. Симкин

Редактор издательства Н.В. Максименко

Компьютерный набор М.В. Березина

Темплан 2005 г., п.249

__________________________________________________________

Подписано в печать __.__.05. Формат Бумага офсетная. Офсетная печать. Усл.печ.л. 1,63. Уч.-изд.л. 1,63 Тираж 30 экз. Заказ Бесплатно.

Брянский государственный технический университет.

241035, Брянск, бульвар 50-летия Октября, 7, БГТУ. 54-90-49.

Лаборатория оперативной полиграфии БГТУ, ул. Институтская, 16.

ВВЕДЕНИЕ

Конечные распознающие автоматы могут быть реализованы как в виде программы, так и аппаратными методами.

В данной расчетно-графической работе необходимо синтезировать комбинационную схему распознающего конечного автомата и начертить его принципиальную схему с использованием библиотеки интегральных микросхем.

Индивидуальным заданием для каждого студента является орграф распознающего конечного автомата, полученный в процессе выполнения курсовой работы по дисциплине «Теория языков программирования и методы трансляции». В ходе выполнения расчетно-графической работы необходимо представить автомат в виде автоматной сети Петри, составить схему размещений автомата, построить структурную и функциональную схемы автомата. На основании полученных результатов необходимо синтезировать комбинационную схему конечного автомата и начертить его принципиальную схему.

ЦЕЛЬ РАБОТЫ

Целью данной работы является:

1) изучение принципов реализации автоматов аппаратными методами;

2) изучение принципов построения сетей Петри для анализа конечных автоматов;

3) освоение способов размещения состояний автомата;

4) освоение методов синтеза комбинационных схем распознающего конечного автомата;

5) освоение принципов принципиальной схемы распознающего конечного автомата.

Продолжительность работы 26 часов.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1) изучение теоретической части методических указаний;

2) построение сети Петри для распознающего конечного автомата в соответствии с индивидуальным заданием;

3) размещение состояний автомата;

4) определение функций возбуждения;

5) синтез комбинационной схемы автомата;

6) построение принципиальной схемы автомата.

ИСПОЛЬЗОВАНИЕ СЕТЕЙ ПЕТРИ ПРИ ПЕРЕХОДЕ

ОТ ГРАММАТИКИ К МИНИМАЛЬНОМУ АВТОМАТУ

Для построения сети Петри рассмотрим полученную в курсовой работе по дисциплине «Теория языков программирования и методы трансляции» праволинейную грамматику G”. Это можно сделать, если поставить в соответствие нетерминальным символам места в сети, а терминальным символам – переходы сети. Обозначим места кружками, а переходы – прямоугольниками (полочками). Будем помечать места и переходы соответствующими терминальными и нетерминальными символами. Поскольку сеть Петри – двудольный граф, соединение дугами мест разрешается только через переходы, а переходов - через места.

Если в правой части некоторого правила вывода из R имеет место катенация терминалов, то в сети Петри между переходами, помеченными терминалами, появляются дополнительные позиции. Эти позиции помечаются символами левой части правила вывода с верхними индексами 1,2,…. Поэтому фрагмент сети Петри, соответствующий первому правилу вывода (S 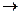x3, x2, x1, A), будет иметь следующий вид (рис.1).

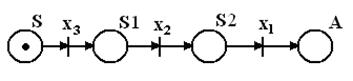
Рис. 1

При построении остальных фрагментов сети Петри, соответствующих последующим правилам вывода, можно использовать ранее обозначенные места, но не переходы. Таким образом, места могут иметь по несколько входящих и исходящих дуг, но переходы – только по одной входящей и не более одной исходящей дуги (исходящей дуги может не быть, если в правой части правила вывода отсутствует замыкающий нетерминал).

Построим по полученным правилам вывода R’ сеть Петри (рис.2).

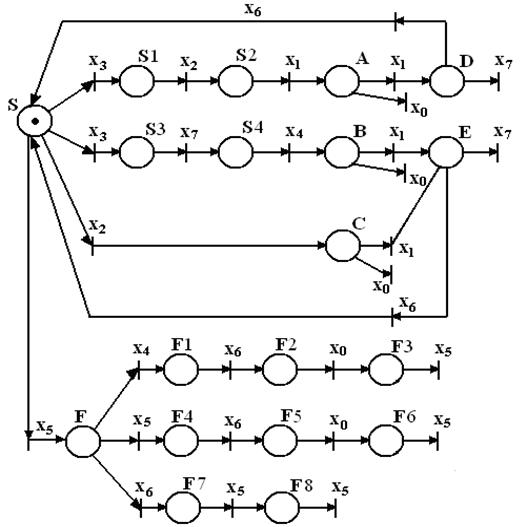
Рис. 2

Построенная сеть представляет собой автоматную сеть Петри, и места можно трактовать как состояния конечного автомата, а переходы – как входные символы. Чтобы обеспечить полное соответствие построенной сети Петри автомату Мура, необходимо ввести не показанную на рис.2 заключительную позицию Z, в которую можно направить дуги из переходов, не имеющих исходящих дуг.

Если теперь рассмотреть отдельные фрагменты сети рис.2, то нетрудно заметить одинаковые фрагменты: места А, В и С с одинаковыми инцидентными им переходами x₁ и x₀, а также еще два идентичных фрагмента с местами D и Е, каждому из которых инцидентны по два выходных перехода x₆ и x₇. Аналогично можно отметить места F1 и F4, F2 и F5, а также F3, F6 и F8. В то же время места S1 и S3 идентичны по входу, т.е. из места S в места S1 и S3 дуги идут через переходы x₃.

Функционирование сети не изменится, если «склеить» идентичные фрагменты, что будет соответствовать минимизации числа состояний автомата. Источником недетерминированности могут быть места, из которых исходят дуги, являющиеся входящими дугами переходов, помеченных одинаковыми терминалами. В данном случае таким местом является начальное состояние S и переходы x₃. Таким образом, производится устранение недетерминированности. В результате получим сеть Петри с минимальным числом мест (рис.3).

Можно также установить взаимнооднозначное соответствие между сетью рис.3 и исходным орграфом.

Для этого местам сети ставятся в соответствие состояния автомата, а переходам – пометки на дугах.

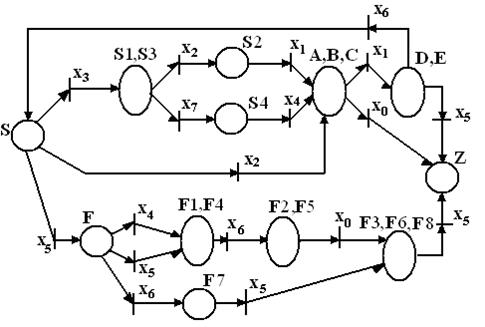
Рис. 3