Виды доказательства. Правила и ошибки.
Аксиомы а) аксиомы ( от греч. axioma – без доказательства) – бездоказательные научные положения, которые принимаются в качестве аргумента при доказательстве других положений. В понятии «аксиома» заключены два логических смысла. Это – «истинное положение, не требующее доказательства» и «отправной пункт доказательства». Именно так понимал аксиому Аристотель, считая истинность аксиом самоочевидной и бесспорной. Понятие "аксиомы" положено в основу аксиоматического метода построения научной теории, когда из исходных аксиом, взятых в качестве основополагающих утверждений, чисто логическим путем выводятся (т.е. доказываются) ее следствия (теоремы). Образцом аксиоматической теории античности является геометрия Евклида и его "Начала". В современных аксиоматических теориях формулируется ряд требований, предъявляемых к формальным системам (непротиворечивость, полнота, независимость). Если на основании данной аксиоматической системы нельзя доказать противоречивые суждения (утверждение или отрицание), то такая система считается непротиворечивой. Если данной системы аксиом достаточно, чтобы вывести все истинные положения в данной научной области, то система аксиом считается полной. Если аксиомы данной системы не выведены из других аксиом этой же научной области, то эта аксиоматическая система является независимой;
Теоремы б) теоремы – доказанные положения науки. Их доказательство принимает вид логического следствия из аксиом;
Законы в) законы – особые положения наук, устанавливающие общие, существенные, необходимые, устойчивые и повторяющиеся связи явлений. Каждая наука имеет свои законы, результирующие определенный вид научно-исследовательской практики. Аксиомы и теоремы также принимают вид законов (аксиома силлогизма, теорема Пифагора);
Факты г) суждения о фактах – раздел научного знания опытно-экспериментального характера (результаты наблюдений, показания приборов, социологические данные, статистика, измерительные данные, данные эксперимента и др.). В качестве аргументов берутся те из суждений о фактах, истинность которых подтверждена на практике.
Определения д) определения. Логический смысл и задача определения нами уже выяснены. Данная логическая операция позволяет формировать в каждой научной области класс определений, которые играют двоякую роль: с одной стороны они помогают специфицировать предмет и отличить его от других предметов данной области, а, с другой стороны, расширять объем научных знаний, вводя новые определения.
2.2. Аргументы ad hominem (апеллирующие к человеку) касаются характерных черт личности, психологии человека и особенностей публичной речи.
Некорректные аргументы Они имеют своей целью убедить «любой ценой» – ссылкой на авторитет, «игрой на публику», ложным аргументом, угрозой и намеком на последствия, «игрой на чувствах» (жалости, тщеславия, эгоизма), обещаниями и заверениями.
Такие аргументы в логике считаются некорректными, а доказательство с их использованием – неправильным. Подробнее мы к ним вернемся, говоря об ошибках в доказательствах.
Итак, повторим, что доказательство обращает «пристальное внимание» на качество и состав аргументов. Кроме того, форма перехода от посылок доказательства к тезису может быть разной. Она образует третий элемент в структуре доказательства.
3. Форма доказательства, или демонстрация – это способ логической связи аргумента и тезиса доказательства. Это самое общее определение доказательства, которое затем конкретизируется в соответствии с предметом науки. Сама логика исследует два вида доказательства:
3.1. Доказательство прямое, т.е. такое, в котором тезис необходимо следует из аргументов. Прямое доказательство часто принимает вид правильного силлогизма – категорического, условного, условно-категорического, разделительно- категорического, условно-разделительного. Можно утверждать, что модус поненс
| p→q |
| p |
| q |
и модус Barbara (ААА) первой фигуры силлогизма – самые распространенные формы прямого доказательства.
Например, по модусу ААА докажем тезис «2004 год будет високосным».
| Любой год, в числовом выражении которого десятки с единицами | ||
| А | делятся на 4, является високосным | |
| А | В 2004 – десятки и числа делятся на 4 | |
| А | 2004 – високосный год. |
Подумайте... Приведите пример прямого доказательства условно-категорической формы:
| p→q |
| p |
| q |
3.2. Доказательство косвенное или апогагическое (отводящее), в котором истинность тезиса устанавливается не прямо (как в 3.1.), а через
Косвенное доказательство доказательство ложности противоречащего ему антитеза. Тезис и антитезис образуют логическое противоречие (как утверждение и отрицание). В этом и заключается логический смысл косвенного доказательства. Закон непротиворечия запрещает одновременную истинность утверждения и отрицания. Значит, установив логическое значение одного из противоречивых положений, мы можем «автоматически» получить логическое значение другого положения. Если в ходе доказательства утверждается одновременная истинность противоречивых положений, то это противоречит правилам. Такую форму мысли греки
Парадокс назвали парадоксом (от греч. para – два и doxos – мнение). Эта форма мысли активно используется в литературном выражении (метафора), в маркетинге («парадоксальная реклама»), однако в формальной логике она является ошибкой. У
Абсурд парадокса есть латинский «брат» – абсурд (от лат. аbsurdus – глупый, нелепый). Под абсурдом в логике понимается внутренне противоречивое высказывание. Оно также нарушает закон противоречия и побуждает к признанию истинными утверждение и отрицание. Выражение, содержащее такое стремление, называют «абсурдным». Например, абсурдным будет следующее определение: «классическая формальная логика – это многозначная логика», поскольку первая признает «только два значения», а вторая – «только не два значения». Парадокс и абсурд следует отличать от бессмыслицы. «Бессмысленное» в логике –
Бессмыслица это высказывание, истинность либо ложность которого установить невозможно. Оно «без смысла», т.е. искусственно, неадекватно ни реальному, ни воображаемому предмету мысли. «Говорить абсурд» – значит, противоречить себе, а «городить бессмыслицу» – значит отгородить от себя собеседника стеной непонимания. Бессмысленное так же «понятно», как «несъедобное съедобно».
Логический смысл «абсурда» используется в доказательстве. В логике существует вид доказательства «путем приведения к абсурду». Его смысл сводится к установлению противоречивых следствий из доказываемого тезиса. Схематически это выглядит так:
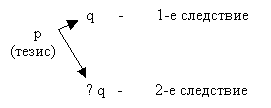
В общем символическом виде схема доказательства выглядит так:
(p → (q& 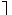 q)) →
q)) → 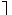 p.
p.
Звучит так: «Если из p следуют противоречивые следствия, то p – ложно».
Так, из нашего определения «формальной логики» вытекают два противоречивых следствия: q – «в ней принимаются два логических значения» и ?q – «в ней не принимаются два логических значения». Положение, из которого выводится противоречие, в логике считается ложным.
Косвенное доказательство является частным случаем «приведения к абсурду», только в нем устанавливаются не противоречивые следствия из одного тезиса, а противоречие единственного следствия реальному положению дел или ранее доказанному. На этом основании заключают о ложности исходного допущения или антитезиса.
Логической схемой косвенного доказательства является правильный отрицающий модус условно-категорического силлогизма – модус толленс:
| Если А, то В | или: | p → q | ||
| не-В | 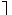 q q | |||
| Следовательно, не-А | 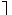 p p |
Косвенное доказательство проводится поэтапно:
1. Требуется доказать тезис А. Докажем его косвенно. Для этого предположим, что истинно его отрицание – не-А.
2. В дальнейшем будем обращаться с не-А как с тезисом. Научное истинное положение должно давать истинные следствия в данной области. Получаем из не-А следствие В.
3. Устанавливаем, что следствие В противоречит ранее доказанному. Следовательно, В – ложно. На логическом языке, оно есть не-В.
4. Ложность следствия (не-В) позволяет с необходимостью заключить о ложности основания (допущения не-А), т.е.:
| Если не-А, то В |
| не-В |
| Следовательно, А |
5. Значит, наше допущение (не-А) оказалось ложным, и истинным будет противоречащее ему высказывание А, что и требовалось доказать.
Упражнения:
1. Определите тезис, аргументы и способ следующих доказательств:
Аргумент - . Тезис - .
1.1. Поскольку геометрическая фигура является треугольником, то сумма внутренних углов этой фигуры равна 180. Прямое доказательство.
1.2. Все области Республики Беларусь имеют свои центры. Их название совпадает с названием области. Значит, областным центром Брестской области является город Брест.
Прямое доказательство.
1.3. Если бы это было сердечное заболевание, то соответствующие признаки были бы видны на кардиограмме. Но кардиограмма - в порядке. Значит, это - не сердечный приступ.
Косвенное доказательство.
ТЕМА № 27
"Опровержение как вид аргументации".
План:
1. Определение опровержения и его структура.
2. Виды опровержения. Правила и ошибки.
Определение опровержения и его структура.
Опровержение – это логическая операция по установлению ложности тезиса. Задача опровержения – установить ложность выдвинутого положения или его недоказанность. Доказать тезис А – значит обосновать его истинность, а опровергнуть тезис А – значит обосновать его ложность. Любое положение может быть подвергнуто двум видам аргументации. Либо будут найдены аргументы, подтверждающие выдвинутое в диалоге положение, либо будут указаны аргументы против данного положения (контраргументы), т.е. опровергающие его. На практике опровержение используется так же широко, как и доказательство, и имеет такую же структуру.
Структура опровержения
Структура опровержения В структуру опровержения входят:
1. Тезис – положение, высказывание, которые необходимо опровергнуть;
2. Аргументы – положения, истинные суждения, при помощи которых опровергается тезис. Аргументы выступают основанием опровержения;
3. Форма опровержения или демонстрация – логический способ связи аргументов и тезиса опровержения. Опровержение может иметь два вида:
3.1. Прямое опровержение тезиса означает обоснование ложности тезиса и истинности антитезиса. Оно начинается с допущения истинным опровергаемого тезиса. Из него выводятся следствия. («Пусть то, в чем Вас обвиняют - истина. Но тогда должны быть следствия…» – это ход рассуждения по логике опровержения). Затем устанавливается несоответствие хотя бы одного из следствий действительному положению вещей или ранее доказанному. («Но эти следствия отсутствуют или противоречат фактам…»). На основании чего из ложности следствия заключают о ложности основания, т.е. допущении истинности тезиса. Значит, тезис ложен, т.е. опровергнут.
Поэтапно это выглядит следующим образом:
а) необходимо опровергнуть тезис А;
б) допускаем, что А – истинно;
в) из А получаем следствия, одно из которых (В) – ложно, т.е. не-В;
г) от ложности следствия заключаем к ложности основания:
| Если А, то В |
| не-В |
| Следовательно, не-А |
д) значит, А (тезис опровержения) – ложно, что и требовалось обосновать.
Нетрудно заметить, что прямое опровержение и косвенное доказательство связаны по смыслу. Например, опровергнуть обвинение в убийстве означает доказать невиновность и, наоборот, доказать вину означает опровергнуть невиновность.
Прямым опровержением будет следующее рассуждение: «Предположим, что он действительно убил этого человека. Но в этом случае должны быть следы преступления, мотив, орудие. Ничего этого нет. Значит, нет и состава преступления».
3.2. Косвенное опровержение тезиса означает доказательство истинности антитезиса. Если удается обосновать ложность тезиса, то по закону непротиворечия заключают об истинности антитезиса. Как видим, логический смысл «косвенного опровержения тот же, что и в косвенном доказательстве. Разными являются логические задачи, стоящие перед доказательством и опровержением:
Косвенное опровержение имеет следующую структуру:
а) необходимо опровергнуть тезис А;
б) допускаем истинность антитезиса не-А;
в) из не-А получаем следствия, одно из которых (В) – ложно, т.е. не-В;
г) из ложности следствия заключаем о ложности основания (допущения истинности не-А):
| Если не-А, то В |
| не-В |
| Следовательно, А |
д) значит, наше допущение (не-А) оказалось ложным и по закону непротиворечия истинным будет противоречащее ему высказывание А, что и требовалось обосновать.
Например, преподаватель хочет опровергнуть заявление студента, что он «знает предмет». Он может делать это прямо, допуская, что он знает этот предмет и установить ложные следствия (отсутствие ответа на вопрос). А может делать это косвенно, следуя логике косвенного опровержения.
Подумайте... Приведите случаи опровержения из учебной практики.
Кроме опровержения тезиса могут быть опровергнуты также аргументы и демонстрация. При опровержении аргументов устанавливается их ложность. Ложность аргументов не означает ложности тезиса, однако указывает на некорректность операции опровержения. При опровержении демонстрации выявляется неправильность связи аргументов и тезиса. Например, вместо модуса-толленса вывод может осуществляться по одному из неправильных модусов условно-категорического силлогизма. Опровержение демонстрации также не означает опровержения тезиса. Однако очевидно, что правильность демонстрации влияет на корректность опровержения в целом. В мышлении и языке познавательное значение опровержения чрезвычайно велико, ибо с помощью данной логической операции удается сократить количество ложных высказываний и заблуждений.
