Обозначение класса точности

Практическое занятие № 6 КЛАССЫ ТОЧНОСТИ СРЕДСТВ ИЗМЕРЕНИЙ

Учет всех метрологических характеристик средств измерений – сложная процедура, оправданная при измерениях высокой точности в метрологической практике. На производстве, как правило, такая точность не нужна. Большинство измерений являются однократными, поэтому за их результат принимается то значение величины, которое непосредственно снято с прибора (без обработки и оценивания погрешности, так как в этом нет необходимости). Но это не означает, что погрешности результатов данного вида измерений неизвестны. Они регламентируются заранее (до выполнения измерений) выбором необходимых по точности средств измерений. Поэтому для средств измерений, используемых в повседневной практике, принято деление по точности на классы.

Общие положения

Класс точности

Класс точности – обобщенная характеристика всех средств измерений данного типа, обеспечивающая правильность их показаний и устанавливающая оценку снизу точности показаний.

В стандартах на средства измерений конкретного типа устанавливаются требования к метрологическим характеристикам, в совокупности определяющие класс точности средств измерений этого типа. Например, у плоскопараллельных концевых мер длины такими характеристиками являются пределы допускаемых отклонений от номинальной длины и плоскопараллельности; пределы допускаемого изменения длины в течение года.

Устанавливая класс точности, нормируют пределы допускаемой основной погрешности. Ее дольные значения принимают в качестве пределов допускаемых дополнительных погрешностей.

Пределы допускаемых погрешностей выражают в форме абсолютных, приведенных или относительных погрешностей. Это зависит от характера изменения погрешности (в пределах диапазона измерений), назначения и условий применения средств измерений.

Если погрешность результатов измерений выражают в единицах измеряемой величины (например, при измерении длины, массы), то пределы допускаемых погрешностей выражают в форме абсолютных погрешностей.

Если границы абсолютных погрешностей средств измерений остаются практически неизменными, применяют форму приведенных погрешностей, если же эти границы нельзя считать постоянными – форму относительных погрешностей.

Абсолютная погрешность прибора

Абсолютная погрешность прибора (меры) Δ – разность между показанием прибора x_ПР (номинальным значением меры) и истинным значением измеряемой (воспроизводимой) x величины:

Δ = x_ПР – x. (15)

Пределы допускаемой абсолютной основной погрешности Δ устанавливают в зависимости от характера изменения погрешности в диапазоне измерений. Если погрешности не зависят от значения измеряемой величины x, то нормируют только границы:

Δ = ±a, (16)

где a – положительное число, не зависящее от x.

Если же с увеличением x погрешность возрастает линейно, то ее пределы устанавливают по формуле

Δ = ±(a + bx), (17)

где Δ – пределы допускаемой абсолютной основной погрешности, выраженной в единицах измеряемой величины на входе (выходе) или условно в делениях шкалы;

x – значение измеряемой величины на входе (выходе) средств измерений или число делений, отсчитанных по шкале;

a, b – положительные числа, не зависящие от x.

Например, для генератора низкой частоты Г3-36: Δ = ±(0,03f + 2) Гц, где f – значение частоты.

Относительная погрешность

Относительная погрешность δ – отношение абсолютной погрешности Δ к значению измеряемой величины x:

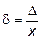. (18)

Пределы допускаемой относительной основной погрешности δ, если границы абсолютных погрешностей Δ можно полагать практически неизменными, находят по формуле

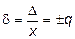, (19)

Если границы абсолютных погрешностей Δ можно полагать меняющимися линейно, пределы допускаемой относительной основной погрешности δ находят по формуле

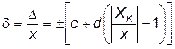, (20)

где δ – пределы допускаемой относительной основной погрешности, %;

q – отвлеченное положительное число, выбираемое из ряда, аналогичному ряду для p;

X_K – больший (по модулю) из пределов измерений;

c, d – положительные числа, выбираемое из ряда, аналогичному ряду для p;

c = b + d; 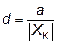. (21)

При постоянной абсолютной погрешности Δ (16) (рисунок 35, штриховые линии) относительная погрешность δ (18) убывает в гиперболической зависимости от измеряемой величины x (рисунок 36, штриховые линии). Если абсолютная погрешность Δ линейно увеличивается с ростом измеряемой величины x, например, по уравнению (17) (рисунок 35, сплошные линии), относительная погрешность δ (18) также убывает по гиперболической зависимости, но гипербола имеет более высокую кривизну (рисунок 36, сплошные линии).

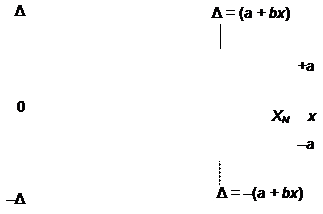
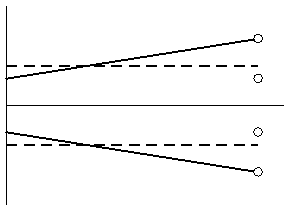
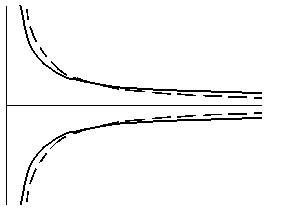
Рисунок 35 – Абсолютная погрешность Δ: постоянная (16) (штриховые линии); линейно возрастающая (17) (сплошные линии)

Рисунок 36 – Относительная погрешность δ: при постоянной абсолютной погрешности Δ (16) (штриховые линии); при линейно возрастающей абсолютной погрешности Δ (17) (сплошные линии)

При выборе прибора для измерений следует учитывать, что при постоянной абсолютной погрешности Δ на различных отметках шкалы будут соответствовать разные значения относительной погрешности δ (см. рисунки 35 и 36).

Пример

Для вольтметра со шкалой 0-150 В класса точности 1,5 основная предельная абсолютная погрешность Δ равна 2,25 В. Относительная погрешность δ (%), на отметках шкалы 25 и 100 В будет соответственно

δ₂₅ = ± (Δ/x)⋅100 = ± (2,25/ 25)⋅100 = ± 9 %;

δ₁₀₀ =± (2,25/100)⋅100 = ± 2,25 %.

С целью уменьшения относительной погрешности δ надо выбирать верхний предел шкалы измерительного прибора таким, чтобы ожидаемое значение измеряемой величины (показание) находилось в последней трети (или половине) ее.

Приведенная погрешность

Указание абсолютной Δ погрешности или относительной δ не позволяет сравнивать между собой по точности приборы с разными диапазонами измерений X_K. Поэтому для электроизмерительных приборов, манометров, приборов измерения физико-химических величин и др. характеристикой точности служит приведенная погрешность γ.

Приведенная погрешность γ – отношение абсолютной погрешности Δ к нормирующему значению X_N, в качестве которого выбирают верхний предел или диапазон измерений, длину шкалы и т.д.

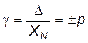, (22)

где γ – пределы допускаемой приведенной основной погрешности, %;

Δ – пределы допускаемой абсолютной основной погрешности, устанавливаемые по формуле (1);

X_N – нормирующее значение, выраженное в тех же единицах, что и Δ;

p – отвлеченное положительное число, выбираемое из ряда 1·10ⁿ; 1,5·10ⁿ; (1,6·10ⁿ); 2·10ⁿ; 2,5·10ⁿ; (3·10ⁿ); 4·10ⁿ; 5·10ⁿ; 6·10ⁿ (n = 1, 0, –1, –2 и т.д.).

Нормирующее значение X_N определяется, исходя из вида шкалы измерительного прибора:

1) шкала равномерная, практически равномерная или степенная – если нулевое значение входного (выходного) сигнала находится на краю или вне диапазона измерений, нормирующее значение X_N устанавливают равным большему из пределов измерений или равным большему из модулей пределов измерений, если нулевое значение находится внутри диапазона измерений;

2) шкала электроизмерительного прибора равномерная, практически равномерная или степенная и нулевой отметкой внутри диапазона измерений – нормирующее значение X_N устанавливают равным сумме модулей пределов измерений;

3) шкала с условным нулем (например, термометр с пределами измерений от 5 до 50 °С) – нормирующее значение X_N устанавливают равным модулю разности пределов измерений;

4) шкала существенно неравномерная – нормирующее значение X_N устанавливают равным всей длине шкалы или ее части, соответствующей диапазону измерений.

Выражение пределов допускаемой погрешности в форме приведенных γ и относительных δ погрешностей является предпочтительным, так как они позволяют выражать пределы допускаемой погрешности числом, которое остается одним и тем же для средств измерений одного уровня точности, но с различными верхними пределами измерений.

Обозначение класса точности

В связи с большим разнообразием средств измерений и их метрологических характеристик ГОСТ 8.401-80 "Государственная система обеспечения единства измерений. Классы точности средств измерений. Общие требования" определены способы обозначения классов точности. Выбор способа зависит от того, в каком виде нормирована погрешность средства измерения. Правила построения и примеры обозначения классов точности в документации и на средствах измерений приведены в таблице 8.

Для средств измерений, пределы допускаемой основной погрешности которых выражают в форме приведенной γ или относительной δ погрешности, классы точности обозначают числами, равными этим пределам в процентах. Чтобы отличить относительную погрешность δ от приведенной γ, на средстве измерений ее обводят кружком (см. таблицу 8). С той же целью под обозначением класса точности на средства измерений ставят знак “V” – это значит, что в случае обозначения приведенной погрешности γ предел абсолютной погрешности Δ приведен к длине шкалы или к ее части (X_N), а не к номинальной точке шкалы.

Таблица 8 – Правила построения и примеры обозначения классов точности в документации и на средствах измерений по ГОСТ 8.401-80

Форма выражения погрешности	Пределы допускаемой основной погрешности	ПРИМЕРЫ
пределов допускаемой основной погрешности, %	обозначения класса точности
в документации	на средстве измерений
Приведенная	По формуле (22):
	шкала равномерная, практически равномерная или степенная	γ = ±1,5	Класс точности 1,5	1,5
	шкала существенно неравномерная	γ = ±0,5	Класс точности 0,5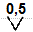
Относительная	По формуле (19)	δ =±0,5	Класс точности 0,5
	По формуле (20)		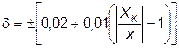Класс точности 0,02/0,01	0,02/0,01
Абсолютная	По формуле (15) или (16)		Класс точности М	М
Относительная	Заданы графиком, таблицей или формулой кроме формул (19) и (20)		Класс точности С	С

В случае относительной погрешности измерительного прибора δ, определяемой по формуле (20), его класс точности обозначают как "c/d". Например, 0,02/0,01 означает: c = 0,02; d = 0,01).

Примеры

Отсчет по шкале прибора с пределами измерений 0-50 и равномерной шкалой равен 25. Пренебрегая другими погрешностями измерений, оценить пределы допускаемой абсолютной погрешности этого отсчета для прибора класса точности 0,02/0,01; 0,5; 0,5.

1. Для прибора класса точности 0,02/0,01 (20)

.

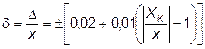Здесь x = 25; X_К = 50; c = 0,02; d = 0,01 и δ указывается в процентах, поэтому

.

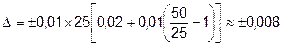2. Для прибора класса точности 0,5 (19)

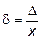, поэтому Δ = ± 0,01 ´ 25 ´ 0,5 = ±0,13.

3. Для прибора класса точности 0,5 (22)

.

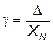По ГОСТ 8.401-80 для средств измерений с равномерной шкалой нормирующее значение X_N устанавливают равным большему из пределов измерений. Поэтому X_N = 50, тогда

Δ = ± 0,01 ´⋅50 ´⋅0,5 = ± 0,25.

Для средств измерений, пределы допускаемой основной погрешности которых принято выражать в форме абсолютных погрешностей Δ (15) или (16), классы точности обозначают документации прописными буквами латинского алфавита или римскими цифрами. Истинное значение абсолютной погрешности Δ указывают в документации на средство измерения.

Такое же обозначение (прописными буквами латинского алфавита или римскими цифрами) применяют в отношении средств измерений, пределы допускаемой основной погрешности которых принято выражать в форме относительных погрешностей δ, если они установлены в виде графика, таблицы или формулы, кроме формул (19) и (20).

В необходимых случаях к обозначению класса точности буквами латинского алфавита допускается добавлять индексы в виде арабской цифры. Классам точности, которым соответствуют меньшие пределы допускаемых погрешностей, должны соответствовать буквы, находящиеся ближе к началу алфавита, или цифры, означающие меньшие числа.

Условные обозначения классов точности наносят на циферблаты, щитки и корпуса средств измерений, а также приводят в нормативно-технической документации.

Пример

Измеряется ток I в пределах от 0,1 до 0,5 мA. Требуется, чтобы относительная погрешность измерения тока δ не превышала 1%. Какой класс точности должен быть у миллиамперметра с конечным значением шкалы I_НОМ = 0,5 мA?

В начале шкалы прибора относительная погрешность измерения 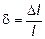больше, так как значение абсолютной погрешности ΔI по всей шкале прибора примерно одно и то же. Поэтому при I = 0,1 мA погрешностьΔI = 0,01´0,1´10^–3 = 10^–6 A . Класс точности прибора находим по основной приведенной погрешности:

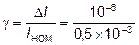= 0,002.

Следовательно, класс точности прибора должен быть 0,2.

Контрольные вопросы

1. Что такое класс точности и что он нормирует?

2. Что такое абсолютная, относительная и приведенная погрешность?

3. В чем недостатки установление основной погрешности в форме абсолютной погрешности?

4. Варианты установления абсолютной и относительной погрешности.

5. Взаимосвязь относительной и абсолютной погрешностей (пояснить графики изменения указанных погрешностей в зависимости от измеряемой величины)

6. Способы установления нормирующего значения при определении приведенной погрешности.

7. Обозначение классов точности средств измерения.

З А Д А Ч А № 8

При поверке амперметра методом сличения с верхним пределом измерения X_ПРЕД в десяти равномерно расположенных точках диапазона значений X₁-X₁₀получили соответственно показания образцового прибора X_1.ОБР-X_10.ОБР(см. таблицу). Определить:

а) для поверяемого прибора абсолютную и относительную погрешности в каждой указанной точке, построить графики погрешностей;

б) класс точности прибора по результатам поверки.

Варианты задачи приведены в таблице 9. Условия задачи и результаты решения занести в протокол (таблица 10).

Таблица 9 – Варианты задачи № 8

	Вариант (XПРЕД)
№	1 (30 мА)	2 (100 мА)	3 (150 мА)	4 (200 мА)	5 (250 мА)	6 (300 мА)	7 (400 мА)
	Xi	Xi.ОБР	Xi	Xi.ОБР	Xi	Xi.ОБР	Xi	Xi.ОБР	Xi	Xi.ОБР	Xi	Xi.ОБР	Xi	Xi.ОБР
		2,65		9,85		14,65		21,65		25,40		28,25		41,35
		5,85		20,15		28,25		42,05		51,15		57,65		82,55
		8,95		29,80		44,50		61,95		73,45		92,55		122,40
		11,90		39,65		59,50		79,65		98,25		121,50		159,35
		15,05		50,05		74,35		98,55		124,55		148,50		202,65
		18,15		59,65		91,35		117,65		151,65		181,35		241,65
		21,05		71,65		104,15		141,55		173,85		212,55		282,55
		24,15		80,15		121,20		161,45		198,30		236,50		322,65
		27,20		90,25		134,15		177,65		224,15		273,20		364,40
		30,05		99,85		149,55		197,55		252,25		303,55		400,55
	Вариант (XПРЕД)
№	8 (500 мА)	9 (600 мА)	10 (700 мА)	11 (800 мА)	12 (900 мА)	13 (1 А)	14 (400 мА)
	Xi	Xi.ОБР	Xi	Xi.ОБР	Xi	Xi.ОБР	Xi	Xi.ОБР	Xi	Xi.ОБР	Xi	Xi.ОБР	Xi	Xi.ОБР
		53,55		62,50		62,50		75,00		87,50	0,1	0,12		3,45
		102,30		121,55		121,55		145,86		170,17	0,2	0,19		7,61
		152,65		183,65		183,65		220,38		257,11	0,3	0,29		11,64
		201,55		237,55		237,55		285,06		332,57	0,4	0,40		15,47
		252,40		298,45		298,45		358,14		417,83	0,5	0,51		19,57
		303,85		354,60		354,60		425,52		496,44	0,6	0,61		23,60
		348,45		418,65		418,65		502,38		586,11	0,7	0,73		27,37
		405,10		478,50		478,50		574,20		669,90	0,8	0,85		31,40
		453,15		543,00		543,00		651,60		760,20	0,9	0,96		35,36
		504,25		602,60		602,60		723,12		843,64	1,0	1,05		39,07
	Вариант (XПРЕД)
№	15 (50 мА)	16 (60 мА)	17 (75 мА)	18 (80 мА)	19 (25 мА)	20 (10 мА)	21 (15 мА)
	Xi	Xi.ОБР	Xi	Xi.ОБР	Xi	Xi.ОБР	Xi	Xi.ОБР	Xi	Xi.ОБР	Xi	Xi.ОБР	Xi	Xi.ОБР
		4,48		5,49	7,5	7,99		7,98	2,5	2,40		1,90	1,5	0,77
		9,89		12,07	15,0	15,87		16,31	5,0	4,41		2,98	3,0	3,48
		15,13		18,25	22,5	22,81		23,71	7,5	7,43		2,39	4,5	4,17
		20,11		24,98	30,0	29,41		32,76	10,0	10,09		4,20	6,0	5,81
		25,43		30,21	37,5	37,70		39,04	12,5	13,13		5,80	7,5	6,56
		30,67		36,71	45,0	44,95		48,60	15,0	15,15		5,86	9,0	9,91
		35,57		41,15	52,5	51,84		56,87	17,5	17,29		7,38	10,5	9,70
		40,81		47,70	60,0	59,44		64,90	20,0	20,22		8,57	12,0	11,54
		45,97		54,35	67,5	67,29		71,10	22,5	22,48		9,33	13,5	13,89
		50,78		60,56	75,0	75,05		80,83	25,0	24,77		10,82	15,0	15,83
	Вариант (XПРЕД)
№	22 (5 мА)	23 (100 мА)	24 (120 мА)	25 (125 мА)	26 (150 мА)	27 (200 мА)	28 (250 мА)
	Xi	Xi.ОБР	Xi	Xi.ОБР	Xi	Xi.ОБР	Xi	Xi.ОБР	Xi	Xi.ОБР	Xi	Xi.ОБР	Xi	Xi.ОБР
	0,5	0,57		9,81		11,61	12,5	12,95		15,98		19,59		24,97
	1,0	0,06		20,22		24,95	25,0	25,63		29,78		39,13		49,10
	1,5	0,98		30,03		36,00	37,5	37,11		44,41		59,93		74,30
	2,0	1,49		39,77		47,44	50,0	49,93		59,34		80,88		99,58
	2,5	1,73		50,86		59,60	62,5	63,34		74,32		100,11		124,95
	3,0	3,98		59,03		72,31	75,0	74,21		89,54		120,74		150,78
	3,5	4,01		70,03		83,83	87,5	87,24		105,79		139,43		174,13
	4,0	3,49		79,35		96,60	100,0	99,45		119,78		159,17		199,45
	4,5	3,60		89,96		107,00	112,5	112,01		134,78		179,21		225,70
	5,0	4,01		99,73		120,03	125,0	124,94		150,71		200,88		249,82

Таблица 10

ПРОТОКОЛ