Глава 4. Элементы теории вероятностей

Основные понятия.

Теория вероятностей есть раздел математики, в котором изучаются только случайные явления (события), происходящие с устойчивой частотой и выявляются закономерности при массовом их повторении.

Под событием понимают все то, что может произойти, а может не произойти. Событие – это возможный исход опыта, явления или наблюдения. Мы не можем заранее сказать, произойдет событие или нет, но мы можем говорить о шансах его наступления.

Пример:Наудачу взятая с полкикнига в библиотеке университета соответствует списку учебной литературы. Здесь опытом является «взятие книги», а событием – соответствие книги списку.

Каждый неразложимый исход опыта называется элементарным событием. Из предыдущего примера – «взятие книги из библиотеки» является совокупностью элементарных событий для множества всех книг библиотеки. Обозначим через 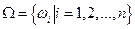множество всех элементарных событий. Оно называется пространством элементарных событий. Для наглядности 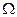изображают в виде некоторой области на плоскости, а элементарные события 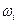-- точками в этой области. Пространство 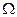представляет все возможные исходы опыта.

Пример:в некоторых играх используется сделанная из однородного материала в виде куба игральная кость, грани которой занумерованы точками. По числу на верхней грани говорят о числе выпавших очков при подбрасывании (от 1 до 6). Каждое из шести событий является элементарным равновозможным событием в условиях данного опыта.

Любое подмножество А множества 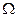называется событием. Событие А наступает тогда, когда результатом опыта является одно из элементарных событий, входящих в А.

Пример:Событие «выпадет четное число очков» произойдет тогда, когда в результате опыта на верхней грани выпадет одно из трех элементарных событий – 2,4,6.

Суммой А+В(или 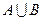) событий А и В называется событие, состоящее из тех элементарных событий, которые входят или в событие А, или в событие В, или в то и другое.

Произведением АВ (или 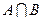) событий А и В называется событие, состоящее из тех элементарных событий, которые входят в оба события А и В.

Разностью А-В (или 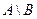) событий А и В называется событие, состоящее из тех элементарных событий, которые входят в А и не входят в В.

Пример:еслисобытие А состоит в попадании в круг, а событие – в ромб, то их сумма заключается в попадании или в круг, или в ромб, а произведение – в попадании в общую часть круга и ромба. Разность – в большую часть круга.

Множество 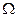называется достовернымсобытием. Пустое множество 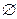-- невозможным.

Пример:событие, заключающееся в том, что взятая книга в библиотеке учебной литературы – пособие, является достоверным, а детектив – невозможным.

События А и В называются несовместными (АВ= 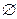), если наступление одного из них исключает возможность наступления другого. В противном случае события называются совместными.

Пример:студент приобрел лотерейный билет. Тогда событие А, состоящее в том, что он выиграет автомобиль, и событие В, состоящее в том, что он выиграет 100руб., являются несовместными. Но если он приобрел два билета, то события А и В совместны.

Событие называется противоположным событию А, если .

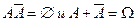Пример: события «студент учится в МГУКи» и «студент не учится в МГУКи» -- противоположные.

События 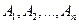образуют полную группу событий, есл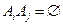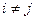и ( ) и .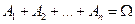

Пример: события, состоящие в выпадении одного из чисел от1 до 6 на игральной кости, образуют полную группу.

Если каждое появление события А сопровождается появлением В, то пишут 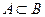и говорят, что А влечет за собой В, или что А является частным случаем В, или что В является следствием события А. Если 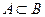, то каждое элементарное событие, входящее в А, содержится в событии В.

В

А

События называются равносильными, если А=В.

Задачи.

1. Пусть А,В,С – три произвольных события. Найти выражения для событий, состоящих в том, что из А,В,С:

а) произошло только А;

б) произошли А и В, но С не произошло;

с) все три события произошли;

д) произошло, по крайней мере, одно из этих событий;

е) произошло, по крайней мере, два события;

ж) произошло одно и только одно событие;

з) произошло два и только два события;

и) ни одно событие не произошло;

2. Доказать, что события А, 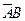, 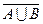образуют полную группу событий.