Формы представления булевых функций

В алгебре логики доказывается, что любую функцию алгебры логики, кроме функции f = 0, можно представить в виде формулы через конъюнкцию, дизъюнкцию и отрицание в виде

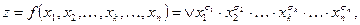(4)

где 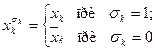— общее обозначение для аргумента x_k и его отрицания.

Логическое суммирование в (4) ведется для тех наборов s₁, s₂, …, s_k, …, s_n, для которых .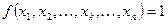

Представление функции алгебры логики в форме (4) называют совершенной дизъюнктивной нормальной формой (СДНФ). Члены, входящие в СДНФ, называют дизъюнктивными членами или конституентами единицы.

Правило построения СДНФ для булевой функции, заданной таблицей истинности:

1) выписать из таблицы те наборы, для которых функция равна единице;

2) для каждого выписанного набора составить конъюнкцию ;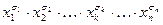

3) соединить полученные конъюнкции знаком дизъюнкции - получается СДНФ искомой функции.

Пример 1. Составить СДНФ для таблично заданной функции (табл. 5).

Таблица 5

х1	х2	х3	z

Используя правило построения СДНФ, получим:

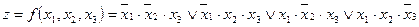
Возможно иное представление функций алгебры логики, называемое совершенной конъюнктивной нормальной формой (СКНФ). В этом случае функция составляется из дизъюнкций, называемых конъюнктивными членами СКНФ или конституентами нуля, объединенных знаком конъюнкции.

Для рассмотренного примера 1 СКНФ функции будет иметь вид:

.

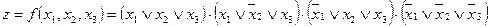Переход от СДНФ к СКНФ представления булевых функций осуществляется так:

· выписывается логическая сумма дизъюнктивных членов, не вошедших в СДНФ, т.е. отрицание функции;

· от полученной логической суммы дизъюнктивных членов берется отрицание.

Пример 2. Построить СКНФ булевой функции по ее СДНФ: 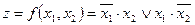. Получим отрицание этой функции:

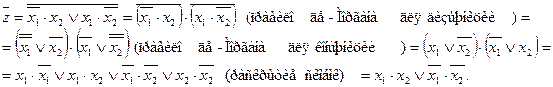
Взяв отрицание от полученного выражения еще раз и использую правило де-Моргана, получим

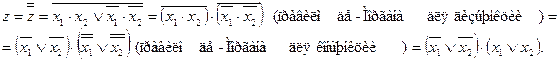
Аналогично осуществляется переход от СКНФ к СДНФ представления функции алгебры логики.