Использованием карт Карно.

Карта Карно построена так, что в ее соседние клетки попадают смежные члены функции — члены, отличающиеся значением одной переменной: в один член эта переменная входит в прямой форме, а в другой — в инверсной. Благодаря этому получается наглядное представление о различных вариантах склеивания смежных членов. В карте Карно содержится столько клеток, сколько комбинаций (наборов) можно составить из прямых и инверсных значений n переменных по n членов в каждой. Так, при n=2 карта содержит четыре клетки (рис.2.4,а), при n= 3 — восемь клеток (рис.2.4,б), при n= 4 - 16 клеток (рис.2.4,в).

Каждая клетка соответствует определенной комбинации переменных. Так, например, левая верхняя клетка карты (см. рис.2.4,а) соответствует комбинации xy,: над столбцом левых клеток указан х, в прямой форме, возле верхней строки записан в прямой форме y. Наборы переменных, на которых F = 1 (в дальнейшем логическую функцию будем обозначать y), т.е. минтермы функции, отмечаются в соответствующих клетках карты 1, в остальные клетки записываются 0 или их оставляют пустыми.

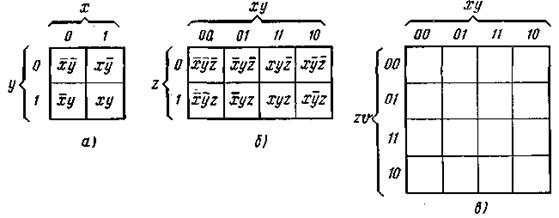
Рис.2.4. Карта Карно функции для двух (а), трех (б) и четырех (в)

переменных

Две стоящие в соседних клетках 1 свидетельствуют о том, что в составе СДНФ имеются члены, отличающиеся значением одной переменной. Такие члены, как известно, склеиваются. Склеивание каждой пары минтермов уменьшает число входящих в них переменных на 1.

Общие правила склеивания членов, занесенных в карту Карно, следующие:

1. Склеиваться могут 2, 4, 8,... членов; при этом соответствующие 1 в клетках для наглядности охватывают прямоугольными контурами.

2. Одним контуром следует объединять максимально возможное количество клеток.

3. Одна и та же 1 может охватываться разными контурами, т. е. один и тот же минтерм может склеиваться с несколькими смежными; последнее объясняется тем, что значение функции не меняется при прибавлении уже имеющихся членов.

4. Крайние строки, а также крайние столбцы карты считаются смежными; их можно таковыми представить, если мысленно свернуть карту в горизонтальный или вертикальный цилиндр.

Функция, минимизированная подобным образом с помощью карты Карно, состоит из суммы простых конъюнкций. Каждая из них получается в результате склеивания членов, которым соответствуют охваченные контуром единицы. В такую конъюнкцию входят только те переменные, значения которых в пределах контура не меняются.

Пример 2.11. Пусть логическая функция задана таблицей истинности (см. табл.2.5). Составить СДНФ и с помощью карт Карно минимизировать ее.

Решение. По приведенной методике составим СДНФ функции:

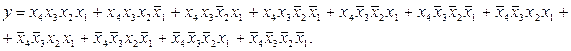(2.11)

Таблица 2.5

Таблица истинности функции y

Номер набора	x4	х3	x2	x1	Y	Номер набора	x4	х3	x2	x1	y

Из табл.2.5 в карту Карно (рис.2.5) занесем значения всех выписанных минтермов. Для удобства проверки в правом верхнем углу клетки указан номер минтерма по его месту в табл.2.5. Контурами охвачены 1, соответствующие склеиваемым минтермам. В результате функция (2.11) представляется в виде

.

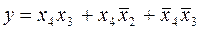Данная форма функции значительно проще первоначальной. Интересно отметить, что она не содержит переменной x₁.

Для получения наиболее простой формы зачастую необходимо при минимизации рассматривать всевозможные варианты склеивания. При числе аргументов, большем четырех, применение карт Карно становится трудоемким, и обычно используют другие методы минимизации.

x2

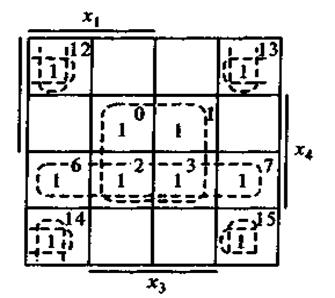
Рис. 2.5. Карта Карно для функции, заданной табл.2.5