Аудиторная самостоятельная работа №11

«Приведение формул алгебры высказываний к КНФ, ДНФ,

СКНФ и СДНФ виду»

Задание №1.

В коробке лежат шары – деревянные и пластмассовые, большие и маленькие, зеленые и красные. Из коробки надо достать шар, соблюдая следующие правила:

1. Шар может быть деревянным только тогда, когда он маленький и зеленый;

2. Если шар маленький, то для того, чтобы он был пластмассовым, достаточно, чтобы он не был зеленым.

3. Если шар маленький и красный, то он деревянный.

Известно, что эти правила сводятся к двум простейшим условиям. Когда же вынули шар, оказалось, что из двух простейших условий выполнено только одно. Кроме того, о вынутом шаре известно, что он либо зеленый, либо большой и деревянный. Какой шар вынули из коробки? (20 баллов)

Задание №2. Приведите формулу к минимальной КНФ:

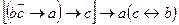(10 баллов)

Задание №3. Приведите формулу к минимальной ДНФ:

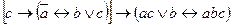(10 баллов)

Задание №4. Приведите формулу к минимальной СКНФ:

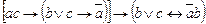(10 баллов)

Аудиторная контрольная работа №2

Примечание 1:номер варианта контрольной работы выбирается в соответствии с порядковым номером (последней цифрой номера) студента в списке группы.

Примечание 2:максимальное количество баллов за каждое из заданий контрольной работы приведено в варианте №1.

Варианты заданий

Вариант № 1

Задание №1. Определите вид категорических суждений, приведите их к канонической форме, укажите, какие термины распределены, а какие нет, изобразите отношения между терминами суждения при помощи кругов Эйлера:а) Иногда люди опаздывают на работу; б) Все распространенные предложения имеют второстепенные члены; в) Некоторые спортсмены не являются мастерами спорта.

(максимальное количество баллов - 3)

Задание №2. Определите вид и структуру сложного высказывания. Запишите его структуру в виде формулы.

«Покрылись зеленью сопки, освобождаются от снега вулканы, в скверы, на улицы Петропавловска-Камчатского в июне высажены деревья, кустарники, готовятся клумбы под цветы». (1 балл)

Задание №3. Произведите отрицание сложного суждения, предварительно записав в виде формулы его структуру:«Если мне дадут отпуск летом, то я поеду отдыхать к морю или по туристической путевке в Карпаты». (2 балла)

Задание №4. Определить с помощью «логического квадрата» отношения между простыми суждениями:

а) Каждый кашалот является водоплавающим; б) Ни один кашалот не является водоплавающим; в) Отдельные кашалоты не являются водоплавающими; г) Некоторые кашалоты — водоплавающие; д) Не все кашалоты дышат жабрами; е) Нет кашалота, который дышал бы жабрами.

(максимальное количество баллов - 4)

Задание №5. Является ли данная формула законом логики? .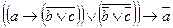

(5 баллов)

Задание №6. При истинности исходного суждения «А знает В, но В не знает А», определите истинностные значения следующих суждений: а) «А и В не знают друг друга»; б) «А и В знают друг друга»; в) «Если В не знает А, то А не знает В».

(3 балла)

Задание №7. Предположим, что мы находимся на острове, на котором живут рыцари и лжецы, и каждый житель острова является либо рыцарем, либо лжецом. Рыцарь всегда говорит правду, а лжец всегда лжет. Используя табличные определения логических союзов, решите задачу:

Вы встречаете двух жителей острова А и В. А говорит: «Если я рыцарь, то В - рыцарь». Кто такой А – рыцарь или лжец? Кто такой В? (5 баллов)

Задание №8. Приведите формулу к минимальной ДНФ: 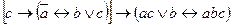(5 баллов)

9. На Олимпиаде по математике была предложена необычная задача.

На столе стояла корзина с яблоками и было известно, что каждое из этих яблок либо большое, либо маленькое; либо сладкое, либо кислое; либо желтое, либо зеленое. На столе лежала инструкция, в которой говорилось, что из корзины можно взять те и только те яблоки, которые удовлетворяют следующим условиям:

1 ) Сладкое яблоко следует взять только при условии, что оно большое и желтое.

2) Если яблоко большое, то сладкий вкус должен быть достаточным признаком желтого цвета.

3) Если яблоко зеленое, то, для того чтобы оно было кислым, необходимо, чтобы оно было маленьким.

Задача состояла в том, чтобы свести требования инструкции к двум простейшим условиям. Кроме того, нужно было узнать, какие яблоки разрешено взять из корзины. Решите эту задачу! (решение задачи требует приведения формулы к СДНФ виду) (15 баллов)

Вариант № 2

Задание №1. Определите вид категорических суждений, приведите их к канонической форме, укажите, какие термины распределены, а какие нет, изобразите отношения между терминами суждения при помощи кругов Эйлера:а) Вода; нагретая до 80⁰, не кипит; б) Цыплят по осени считают; в) Ни один учитель нашей школы не является отличником народного просвещения.

Задание №2. Определите вид и структуру сложного высказывания. Запишите его структуру в виде формулы.

«Поиски врага длились уже три часа, но результатов не дали, а притаившийся враг ничем себя не выдавал».

Задание №3. Произведите отрицание сложного суждения, предварительно записав в виде формулы его структуру:«Неверно, что этот писатель драматург или поэт».

Задание №4. Определить с помощью «логического квадрата» отношения между простыми суждениями:а) Все лыжники — мастера спорта; б) Некоторые лыжники не являются мастерами спорта; в) Ни один лыжник не является мастером спорта; г) Отдельные лыжники — мастера спорта.

Задание №5. Является ли данная формула законом логики? .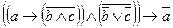

Задание №6. При истинности исходного суждения «А знает В, но В не знает А», определите истинностные значения следующих суждений: а) «Либо А не знает В, либо В не знает А»; б) «В знает А , или А не знает В»; в) «Если А не знает В, то В знает А».

Задание №7. Предположим, что мы находимся на острове, на котором живут рыцари и лжецы., и каждый житель острова является либо рыцарем, либо лжецом. Рыцарь всегда говорит правду, а лжец всегда лжет. Используя табличные определения логических союзов, решите задачу:

Вы встречаете трех жителей острова А, В и С. А говорит: «В - рыцарь». В говорит: «Если А рыцарь, то С - рыцарь», Кто такой А – рыцарь или лжец? Кто такой В? Кто такой С?

Задание №8. Приведите формулу к минимальной КНФ: .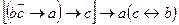

Задание №9.

У Пети был день рождения и он хотел пригласить своих друзей. В связи с этим были высказаны следующие суждения:

Мама сказала: «Если мы пригласим Володю, то надо пригласить и Андрея. А Серёжу приглашать не надо».

Папа сказал: «Неверно, что Андрея или Володю, а также Серёжу можно пригласить тогда и только тогда, когда будет приглашён или Серёжа, или Володя».

Бабушка сказала: «Нельзя пригласить ни Андрея, ни Володю».

Пете это не понравилось, и он сказал, что в качестве инструкции надо взять не эти высказывания, а их отрицания. Родители засмеялись и согласились, но потребовали, чтобы Петя новую инструкцию свёл к простейшим условиям. Какие условия получились? (решение задачи сводится к поиску минимальной КНФ)

Вариант № 3

Задание №1. Определите вид категорических суждений, приведите их к канонической форме, укажите, какие термины распределены, а какие нет, изобразите отношения между терминами суждения при помощи кругов Эйлера:а) Без идеалов не может получиться никакой хорошей действительности; б) Среди ученых встречаются неумные люди; в) Привычка нередко превращается во всепоглощающую страсть.

Задание №2. Определите вид и структуру сложного высказывания. Запишите его структуру в виде формулы.

«Неверно, что бы Иван IV был зол по природе и не заботился об интересах государства, тогда и только тогда, когда Иван IV не был зол по природе или заботился об интересах государства».

Задание №3. Произведите отрицание сложного суждения, предварительно записав в виде формулы его структуру:«Если завтра будет жаркая погода и не будет ветра, то грозы не будет.».

Задание №4. Определить с помощью «логического квадрата» отношения между простыми суждениями:

а) Некоторые люди являются художниками; б) Некоторые люди не относятся к художникам; в) Ни один человек не является художником: г) Каждый человек — художник.

Задание №5. Является ли данная формула законом логики? .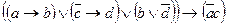

Задание №6. При истинности исходного суждения «А знает В, но В не знает А», определите истинностные значения следующих суждений: а) «А знает В и В не знает А»; б) «А занет В тогда и только тогда, когда В знает А»; в) «Если В знает А, то А не знает В».

Задание №7. Предположим, что мы находимся на острове, на котором живут рыцари и лжецы., и каждый житель острова является либо рыцарем, либо лжецом. Рыцарь всегда говорит правду, а лжец всегда лжет. Используя табличные определения логических союзов, решите задачу:

На острове, населенном рыцарями и лжецами, разнесся слух, что на нем зарыты сокровища. Вы спрашиваете у А: «Есть ли на острове золото?». Ф: «Сокровища на острове есть в том и только в том случае, если я – рыцарь». а) Можно ли определить, кто такой А? б) Можно ли определить, есть ли на острове сокровища?

Задание №8. Приведите формулу к минимальной СДНФ: .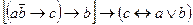

Задание №9.В коробке лежат шары: большие и маленькие, красные и зелёные, тёмные и светлые. Из коробки надо достать шар, удовлетворяющий следующим условиям:

1) Если шар светлый, то он может быть маленьким тогда, когда он красный.

2) Шар может быть большим и светлым, если он зелёный.

3) Если шар большой, то, для того чтобы он был зелёным, достаточно, чтобы он был тёмным.

Свести эти требования к двум простейшим условиям. (решение задачи сводится к поиску минимальной КНФ)

Вариант № 4

Задание №1. Определите вид категорических суждений, приведите их к канонической форме, укажите, какие термины распределены, а какие нет, изобразите отношения между терминами суждения при помощи кругов Эйлера:а) Некоторые лекарства опаснее самих болезней; б) Никакая причина не извиняет невежливости; в) Среда - третий день недели.

Задание №2. Определите вид и структуру сложного высказывания. Запишите его структуру в виде формулы.

«Поиски врага длились уже три часа, но результатов не дали, притаившийся враг ничем себя не выдавал».

Задание №3. Произведите отрицание сложного суждения, предварительно записав в виде формулы его структуру:«Неверно, что этот писатель драматург или поэт».

Задание №4. Определить с помощью «логического квадрата» отношения между простыми суждениями:а) Все лыжники — мастера спорта; б) Некоторые лыжники не являются мастерами спорта; в) Ни один лыжник не является мастером спорта; г) Отдельные лыжники — мастера спорта.

Задание №5. Является ли данная формула законом логики? .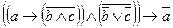

Задание №6. При истинности исходного суждения «А знает В, но В не знает А», определите истинностные значения следующих суждений: а) «Либо А знает В, либо В знает А»; б) «В не знает А , или А знает В»; в) «Если А знает В, то В знает А».

Задание №7. Предположим, что мы находимся на острове, на котором живут рыцари и лжецы., и каждый житель острова является либо рыцарем, либо лжецом. Рыцарь всегда говорит правду, а лжец всегда лжет. Используя табличные определения логических союзов, решите задачу:

Вы встречаете трех жителей острова А, В и С. А говорит: « С - рыцарь». С говорит: «Если А рыцарь, то В - не рыцарь», Кто такой А – рыцарь или лжец? Кто такой В? Кто такой С?

Задание №8. Приведите формулу к минимальной ДНФ: .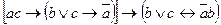

Задание № 9. В ящике лежат шары: синие и красные, большие и маленькие, деревянные и пластмассовые. Предлагается достать шар, соблюдая следующие правила:

1) Чтобы шар был синим, достаточно, чтобы он был большим только при условии, что он пластмассовый.

2) Шар может быть красным или большим, если он деревянный.

3) Чтобы шар был большим, достаточно, чтобы он был деревянным и красным.

Докажите, что эти правила сводятся к двум простейшим условиям. Выясните, какие шары им удовлетворяют. (решение задачи требует приведения формулы к СДНФ виду)