Классификация по ближайшей центроиде
Теперь предположим, что образцы каждого класса образуют шарообразный кластер и что кластеры, соответствующие различным классам, примерно одинакового радиуса и не слишком пересекаются друг с другом. В этом случае запоминать все образцы для каждого класса кажется расточительным. Вместо этого можно использовать для представления каждого класса его центр тяжести. Считается, что неизвестный вектор принадлежит тому классу, центр тяжести которого находится к нему ближе всего.
Использование этого метода позволяет значительно уменьшить и память, и вычисления. Более того, классы здесь разделяются гладкими границами. Отметим, что эти компоненты являются гипермногогранниками, ограниченными гиперплоскостями. (Гипермногогранники — это обобщение выпуклого многогранника для числа измерений больше трех. Они образуются пересечением полупространств.) Чтобы показать, что границы являются гиперплоскостями, предположим, что х — точка на границе между частями, содержащими центроиды 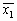 и
и 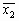 , тогда
, тогда 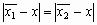 . Возведя в квадрат обе части равенства, получим
. Возведя в квадрат обе части равенства, получим 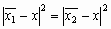 или
или 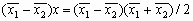 . Это уравнение линейно по х. Оно описывает гиперплоскость с нормалью
. Это уравнение линейно по х. Оно описывает гиперплоскость с нормалью 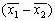 , проходящую через точку
, проходящую через точку 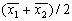 . Таким образом, границей является гиперплоскость, ортогонально секущая пополам отрезок, соединяющую две центроиды.
. Таким образом, границей является гиперплоскость, ортогонально секущая пополам отрезок, соединяющую две центроиды.
Этот простой метод разделения пространства признаков хорошо работает в том случае, когда кластеры симметричны относительно вращения и примерно одинаковых радиусов, или когда они хорошо разделены.

Рис. 1. Диаграмма разброса площадей цитоплазмы и ядра для пяти типов белых кровяных телец. Буква обозначает различные классы, подчеркнутая буква — центроиду. Штриховые линии показывают линейные границы, оптимально разделяющие классы. Несколько образцов классифицировано неверно.
