Построение функциональных логических схем по заданным функциям

При построении отдельных узлов компьютера довольно часто необходимо решить проблему построения функциональных логических схем по заданным функциям. Для этого достаточно условиться, что истинное высказывание соответствует тому, что цепь проводит ток, а ложное – цепь разорвана.

Логические операции конъюнкции, дизъюнкции, инверсии реализуются в ЭВМ с помощью следующих элементарных схем.

Конъюнкция – логический элемент «и»:

Этот элемент выполняет операцию логического умножения (конъюнкция): f = x₁Ù x₂ Ùx₃ Ù…Ùx_n ; и имеет n входов и один выход.

Дизъюнкция – логический элемент «или»:

Этот элемент выполняет операцию логического сложения (дизъюнкция): f = x₁Ú x₂ Úx₃ Ú…Úx_n ; и имеет n входов и один выход.

Инверсия – логический элемент «не»:

Этот элемент выполняет операцию логического отрицания (инверсии): f = 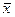; и имеет один вход и один выход.

Сложные функциональные схемы можно конструировать из основных логических элементов, используя основные законы булевой алгебры

Пример выполнения контрольного задания

Задание:

Дана функция,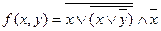

1. Составить функциональную логическую схему по данной функции.

2. Упростить логическую функцию (используя законы булевой алгебры) и выполнить проверку преобразования таблицей истинности.

3. Составить функциональную логическую схему по упрощенной функции.

Выполнение:

1. Составим таблицу истинности для заданной функции:

x	y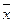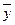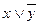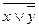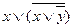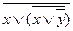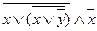

2. Составим функциональную логическую схему по заданной функции:

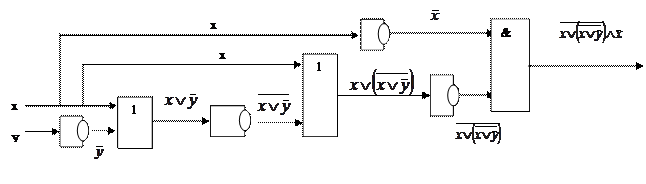
3. Упростим заданную функцию, используя законы булевой алгебры:

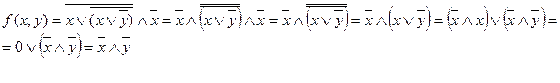
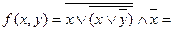
а) по закону де Моргана – 9

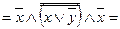
б) по закону идемпотентности - 13

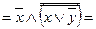
в) закон отрицание отрицания – 1

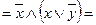
г) закон дистрибутивности – 6

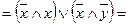
д) свойства 1 и 0 – 19

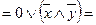
е) свойства 1 и 0 – 16

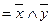
Таким образом, упрощенная функция имеет вид: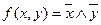

4. Составим таблицу истинности для упрощенной функции:

x	y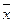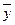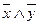

Таким образом, сравнивая таблицы истинности для исходной и упрощенной функций (их последние столбцы) делаем вывод о правильности проведенных преобразований.

5. Составим функциональную логическую схему по упрощенной функции:

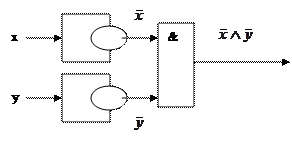
Задание для выполнения контрольной работы

Дана функция f(x,y), номер функции в таблице соответствует порядковому номеру студента по списку.

4. Составить функциональную логическую схему по данной функции.

5. Упростить логическую функцию (используя законы булевой алгебры) и выполнить проверку преобразования таблицей истинности.

6. Составить функциональную логическую схему по упрощенной функции.

Таблица функций.

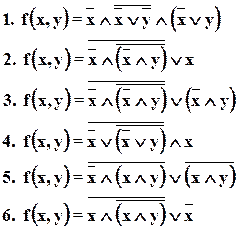
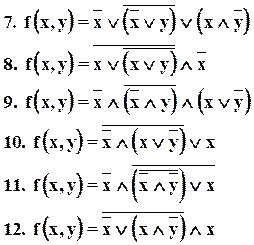
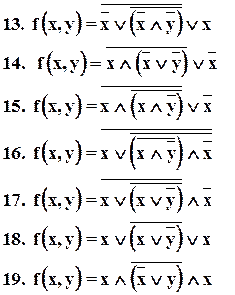
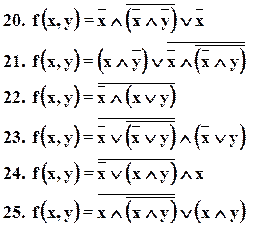
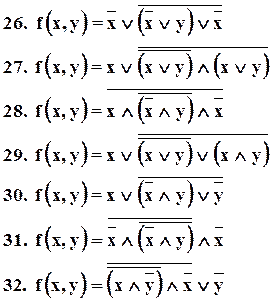
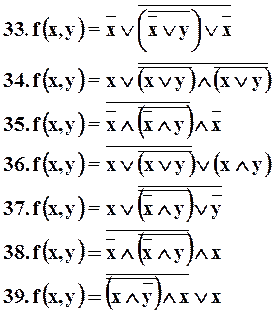
Список литературы

1. Ляхович В.Ф., Краморов С.О. Основы информатики. – Ростов-на-Дону.: Феникс 2003
2. Информатика / Под ред. А.Р. Есаян.: Просвещение, 1991
3. Зварыкин В. М. Основы информатики и вычислительной техники/ В.М. Зварыкин, В.Г. Житомирский. М.П. Лапчик. –М.: Просвещение, 1989

Составитель: Романова Любовь Геннадьевна

ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ.

ЛОГИЧЕСКИЕ ОСНОВЫ ЭВМ.

Учебно-методическое пособие по выполнению контрольного задания по информатике для студентов заочной формы обучения и представительств

инженерных специальностей СГАУ им. Н. И. Вавилова