Основные логические элементы

Логической функцией называется функция нескольких переменных x₁, x₂, …, x_n

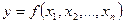, (1)

когда сама функция и независимая переменная могут принимать только два значения: 0 и 1. Такие функции часто называют переключательными функциями.

Любая переключательная функция может быть представлена ком­бинацией только трех основных функций алгебры логики: инверсии, дизъюнкции и конъюнкции. Инверсия является функцией от одной пе­ременой (одноместной функцией). Дизъюнкция и конъюнкция рассма­триваются как функции многих переменных (многоместные функции).

Используя суперпозицию можно в качестве аргумента любой из трех указанных функций задавать произвольную переключательную функцию. При этом инверсия, дизъюнкция и конъюнкция могут рассма­триваться не только как функции, но и как операции, определённые на множестве всех переключательных функций.

Техническим аналогом переключательной функции является комбинационная схема, выполняющая соответствующее этой функции преобразование информации. Элементарные логические операции над дво­ичными переменными(0 и 1) реализуются схемами, которые называют­ся логическими элементами. Число входов логического элемента соответствует числу аргументов воспроизво­димой им булевой функции.

Инвертор.

Логический элемент НЕ называют инвертором, т.к. он инвертирует логическую величину x в :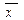

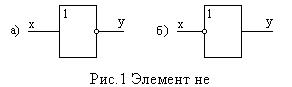
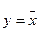(2)

Условное обозначение инвертора показано на рис.1a. Функция инверсии обозначена кружком на выходе схемы. Этот кружок можно перенести и на вход схемы (рис.1б), что является справедливым только в случае инвертора. Инверсия, выполненная дважды, восстанавливает первоначальную величину.

В практической схеме инвертора может быть использован транзистор, выполняющий функции электронного ключа (рис.2а).

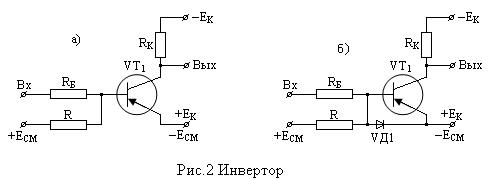
Для реализации двух значений переменной используются два режима работы транзистора: режим отсечки (транзистор закрыт) и режим насыщения (транзистор открыт). Если напряжение U_ВХ=0 (соответствует логическому 0), то под действием напряжения смещения E_CM транзистор будет закрыт, т.е. 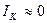. Падение напряжения на резисторе R_К, равно 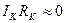. Поэтому напряжение , что соответствует логической 1. При подаче на вход напряжения, со­ответствующего логической 1, транзистор открывается. При этом 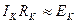, , 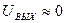что соответствует логическому 0. Рассмотренная схема инвертора представляет собой пример резисторно-транзисторной логики (РТЛ)

Инвертор с электронным ключом на транзисторе собирают и по схеме, показанной на рис.2б. Диод VD₁, включённый с резистором R в цепь делителя для подачи напряжения смещения, ограничивает величину обратного напряжения на эмиттерном переходе транзистора VT₁ (для напряжения смещения диод включен в прямом направлении, поэтому обладает малым сопротивлением R_ПР<<R ) и тем самым обеспечивает надежность работы транзистора в течение длительного времени, т.к. при малом обратном напряжение может произойти про­бой эмиттерного перехода. Резистор R₅ ограничивает величину прямого тока через эмиттерный переход,когда транзистор работает в режименасыщения, определяя в этом режиме I_БН и I_КН = βI_БН.

Дизъюнктор.

Дизъюнктор осуществляет операцию в соответствии с равенст­вом:

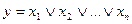(3)

Это значит, что сигнал на выходе дизъюнктора действует тогда, когда имеется сигнал хотя бы на одном из его входов.

Пример комбинационной схемы, реализующей функцию ИЛИ (дизъ­юнкции), приведен на рис.3а, а условное обозначение дизъюнктора показано на рис.3б.

Рис. 3. Элемент или (дизъюнктор)

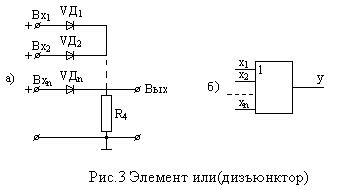
Проанализируем работу схемы дизъюнктора (рис. За).

Для сигнала положительной полярности диод включен в прямом направлении. При этом прямое сопротивление диода R_ПР << R_Н. В результате 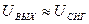. В данном случае напряжение на выход по­падает непосредственно от источника сигнала. Рассмотренная схема представляет собой пример резисторно – диодной логики (РДЛ).

Конъюнктор.

Конъюнктор осуществляет операцию в соответствии с равенст­вом:

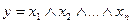(4)

Это значит, что сигнал на выходе конъюнктора действует тогда, и только тогда, когда действует сигналына всех его входах.

Пример комбинационной схемы, реализующей функцию И (конъюн­кцию) приведен на рис.4а, а условное обозначение конъюнктора показано на рис.4б (знак логического умножения - &).

Рис. 4. Элемент и (конъюнктор)

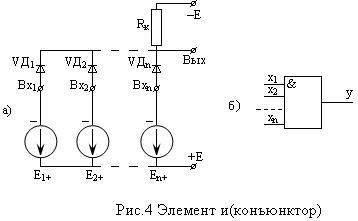
Проанализируем работу схемы конъюнктора (рис.4а).

При отсутствии сигналов на Вх1, Вх2,..., Вхn, все диоды VD1, VD2,…, VDn открыты под действием напряжения Е на выходе внутреннего источника тока. При этом выходное сопротивление схемы 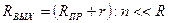(R_ПР – сопротивление диодов в прямом направлении, 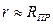- малое внутреннее сопротивление источников сигналов). Напряжение на выходе 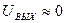(соответству­ет логическому 0). Если на всех входах действует напряжение по модулю большее Е, то все диоды закрыты и выходное сопротивление схемы 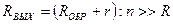(R_ОБР – обратное сопротивление диодов). В этом случае 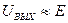(соответствует логической 1). Если хоть одного из напряжений на входе нет, то со­противление соответствующей цепи (R_ПР+r) << R и 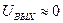. Вданном случае напряжение на выход схемы поступает от внутреннего источника тока Е. Сигналы, подаваемые на входы, переводят ди­оды в закрытое состояние. Рассмотренная схема тоже представляет пример резисторно-диодной логики (РДЛ).