Логические выражения и операции
Логика – это наука о формах и способах мышления. Это учение о способах рассуждений и доказательств.
Законы мира, сущность предметов, общее в них мы познаем посредством абстрактного мышления. Логика позволяет строить формальные модели окружающего мира, отвлекаясь от содержательной стороны.
Мышление всегда осуществляется через понятия, высказывания и умозаключения.
Понятие – это форма мышления, которая выделяет существенные признаки предмета или класса предметов, позволяющие отличать их от других.
Высказывание – это формулировка своего понимания окружающего мира. Высказывание является повествовательным предложением, в котором что-либо утверждается или отрицается.
По поводу высказывания можно сказать, истинно оно или ложно.
П 4.1.Истинное высказывание: «Буква «а» - гласная».
Ложное высказывание: «Компьютер был изобретен в середине XIX века».
Умозаключение – это форма мышления, с помощью которой из одного или нескольких суждений может быть получено новое суждение (знание или вывод).
Алгебра логики отвлекается от смысловой содержательности высказываний и принимает во внимание только истинность или ложность высказывания.
Можно определить понятия логической переменной, логической функции и логической операции.
Логическая переменная – это простое высказывание, содержащее только одну мысль. ЕЕ символическое обозначение – латинская буква (например, A, B, X, Y и т.д.). Значением логической переменной могут быть только константы ИСТИНА или ЛОЖЬ; True (T) или False (F); 1 или 0.
Составное высказывание – это логическая функция, которая содержит несколько простых мыслей, соединенных между собой с помощью логических операций. Ее символическое обозначение – F(A, B,…).
На основании простых высказываний могут быть построены составные высказывания.
Логические операции – это логическое действие.
Рассмотрим три базовые логические операции – отрицание, конъюнкцию, дизъюнкцию и дополнительные – импликацию и эквивалентность.
| A | B | 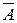 | 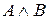 | 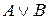 | 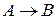 | А↔В |
Если составное высказывание (логическую функцию) выразить в виде формулы, в которую войдут логические переменные и знаки логических операций, то получится логическое выражение, значение которого можно вычислить. Значением логического выражения могут быть только ЛОЖЬ или ИСТИНА. При составлении логического выражения необходимо учитывать порядок выполнения логических операций, а именно:
1) действия в скобках;
2) инверсия, конъюнкция, дизъюнкция, импликация, эквивалентность.
П 4.2.Записать в виде логического выражения следующее высказывание: «Летом Петя поедет в деревню и, если будет хорошая погода, то он пойдет на рыбалку».
1. Проанализируем составное высказывание.
Оно состоит из следующих простых высказываний: «Петя поедет в деревню», «Будет хорошая погода», «Он пойдет на рыбалку». Обозначим их через логические переменные:
А = Петя поедет в деревню;
В = Будет хорошая погода;
С = Он пойдет на рыбалку.
2. Запишем высказывание в виде логического выражения, учитывая порядок действий. Если необходимо, расставим скобки:
F = A Λ (B→C).
П 4.3.Есть два простых высказывания:
А – «Число 10 – четное»
В – «Волк – травоядное животное».
Составьте из них все возможные высказывания и определите их истинность. Ответ:
| AΛB | A V B | 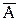 | 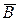 | A → B | A ↔ B |
| Ложь (0) | Истина (1) | Ложь (0) | Истина (1) | Ложь (0) | Ложь (0) |
Тестовые задачи
Составить и записать сложные высказывания из простых с использованием логических операций.
Т 4.1. Неверно, что 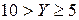 и Z < 0.
и Z < 0.
Варианты ответа:
а) 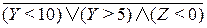 ; б)
; б) 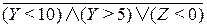 ;
;
в) 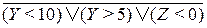 ; г)
; г) 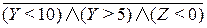
Т 4.2. Z является min (Z, Х, Y).
Варианты ответа:
а) (Z < Y)Λ(Z < X); б) (Z > Y)Λ(Z < X);
в) (Z < Y)V(Z < X); г) (Z < Y)Λ(Z > X).
Т 4.3.А является max (A, B, C).
Варианты ответа:
а) (A > B) Λ (A < C); б) (A > B) Λ (A > C);
в) (A < B) Λ (A > C); г) (A > B) V (A > C).
Т 4.4.Любое из чисел X, Y, Z положительно.
Варианты ответа:
а) (X > 0) Λ (Y > 0) V (Z > 0); б) (X > 0) V (Y > 0) Λ (Z > 0);
в) (X > 0) V (Y > 0) V (Z > 0); г) (X > 0) Λ (Y > 0) Λ (Z > 0).
Т 4.5. Любое из чисел X, Y, Z отрицательно.
Варианты ответа:
а) (X < 0) V (Y < 0) V (Z < 0); б) (X > 0) V (Y < 0) Λ (Z < 0);
в) (X < 0) Λ (Y < 0) V (Z < 0); г) (X < 0) Λ (Y < 0) Λ (Z < 0).
Т 4.6. Все числа X, Y, Z равны 12.
Варианты ответа:
а) (X = 12) V (Y = 12) Λ (Z = 12); б) (X = 12) Λ (Y = 12) V (Z = 12);
в) (X = 12) Λ (Y = 12) Λ (Z = 12); г) (X = 12) V (Y = 12) V (Z = 12).
Т 4.7. Только одно из чисел X, Y отрицательно.
Варианты ответа:
а) (X < 0) Λ (Y > 0) Λ (X > 0) Λ (Y < 0); б) (X < 0) V (Y > 0) V (X > 0) Λ (Y < 0);
в) (X < 0) Λ (Y< 0) V (X > 0) Λ (Y < 0); г) (X < 0) Λ (Y > 0) V (X > 0) Λ (Y < 0).
Т 4.8. Какое логическое выражение соответствует высказыванию: «Точка Х принадлежит интервалу (А, В)»?
Варианты ответа:
а) (X < A) или (X > B); б) (X > A) и (X < B);
в) не (X < A) или (X > B); г) (X > A) или (X > B).
